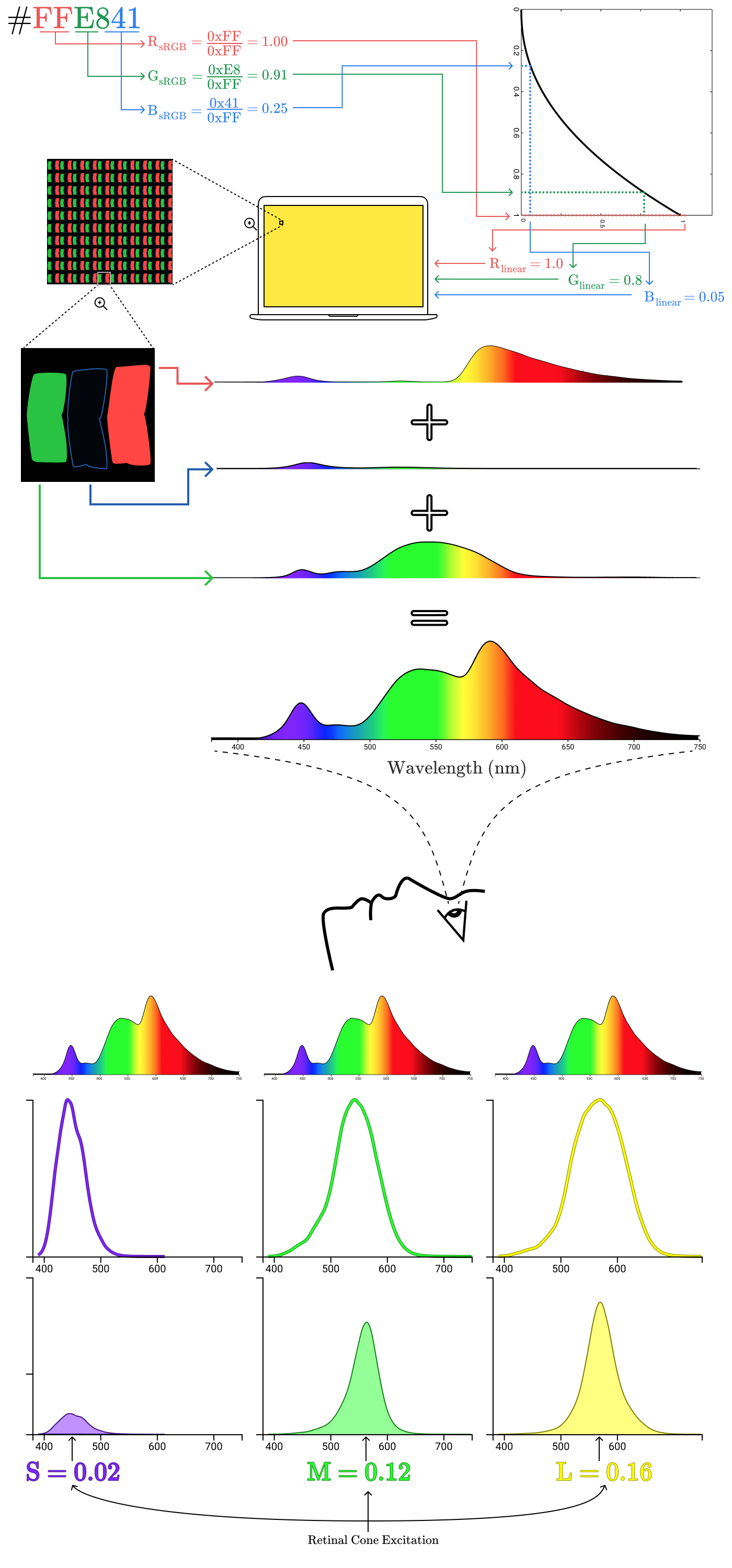
注釈：
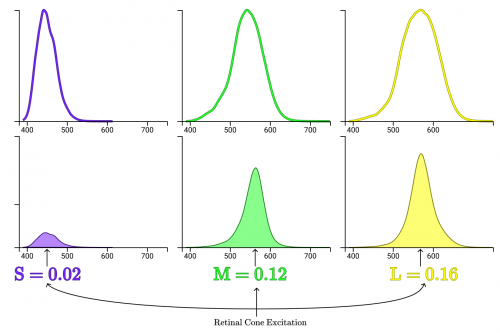
波長（um）
網膜錐体の励起

私たちの目が、 background-color: #9B51E0 を、この紫色だと知覚するのはなぜでしょうか。

長い間、私はその答えを知っていると思っていましたが、よく考え直してみると、かなり大きな思い違いをしていることに気付きました。

そこで、この思い違いを、電磁放射、光生物学、測色学、表示用ハードウェアについて探求しながら解消していこうと思います。本文の構成は次のようになっています。飛ばし読みしたい方は好きな章から読んでください。

• 電磁放射
• 可視光線
• 人間が知覚する輝度
• 色の定量化
• 視覚の生物学的メカニズム
• 色空間
• ライトとギルドの等色実験
• 色空間と色度の可視化
• 色域とスペクトル軌跡
• CIE XYZ色空間
• 画面のサブピクセル
• sRGB
• sRGBヘキサコード
• ガンマ補正
• ヘキサコードから眼球まで
• 輝度設定について
• 書き切れなかったこと
• 参考文献

では、物理学から始めましょう。

電磁放射

電波、マイクロ波、赤外線、可視光線、紫外線、X線、ガンマ線は全て、一種の電磁放射です。どれも名前は違いますが、実は、それぞれの名前は、電磁スペクトルの中の異なる波長範囲に付けられた単なるラベルです。

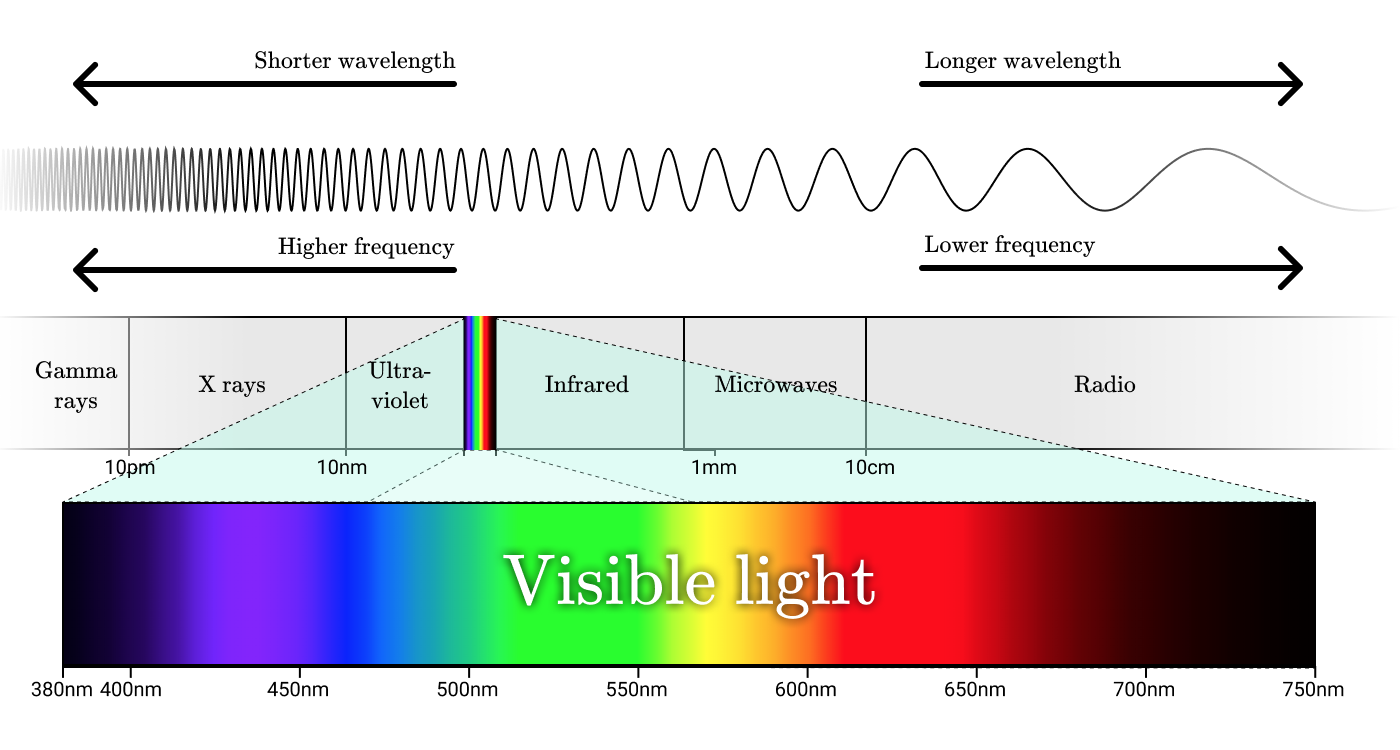
注釈：
短い波長
長い波長
高い周波数
低い周波数
ガンマ線
X線
紫外線
赤外線
マイクロ波
電波
可視光線

電磁スペクトル

電磁放射の最小単位は光子です。光子に含まれるエネルギーは対応する電磁波の周波数に比例し、高エネルギーの光子は高周波数の電磁波に対応します。

色について本当に理解するには、まず、放射について理解する必要があります。白熱電球の放射について、詳しく考えてみましょう。

写真： Alex Iby

電球は、どのくらいのエネルギーを放射しているのでしょうか。ある物体の 放射束 （ Φ e ）は、1秒あたりに放出されるエネルギーの合計で、ワット単位で測られます。100Wの白熱電球の放射束は約80Wで、残りの20Wは、放射されない熱に直接変換されます。

それぞれの波長からのエネルギーがどれぐらいか知るには、 分光放射束 を調べます。ある物体の分光放射束（ Φ e , λ ）は、単位波長あたりの放射束で、通常、ワット/ナノメートル単位で測られます。

この白熱電球の分光束を波長の関数としてグラフにすると、次の図のようになります。

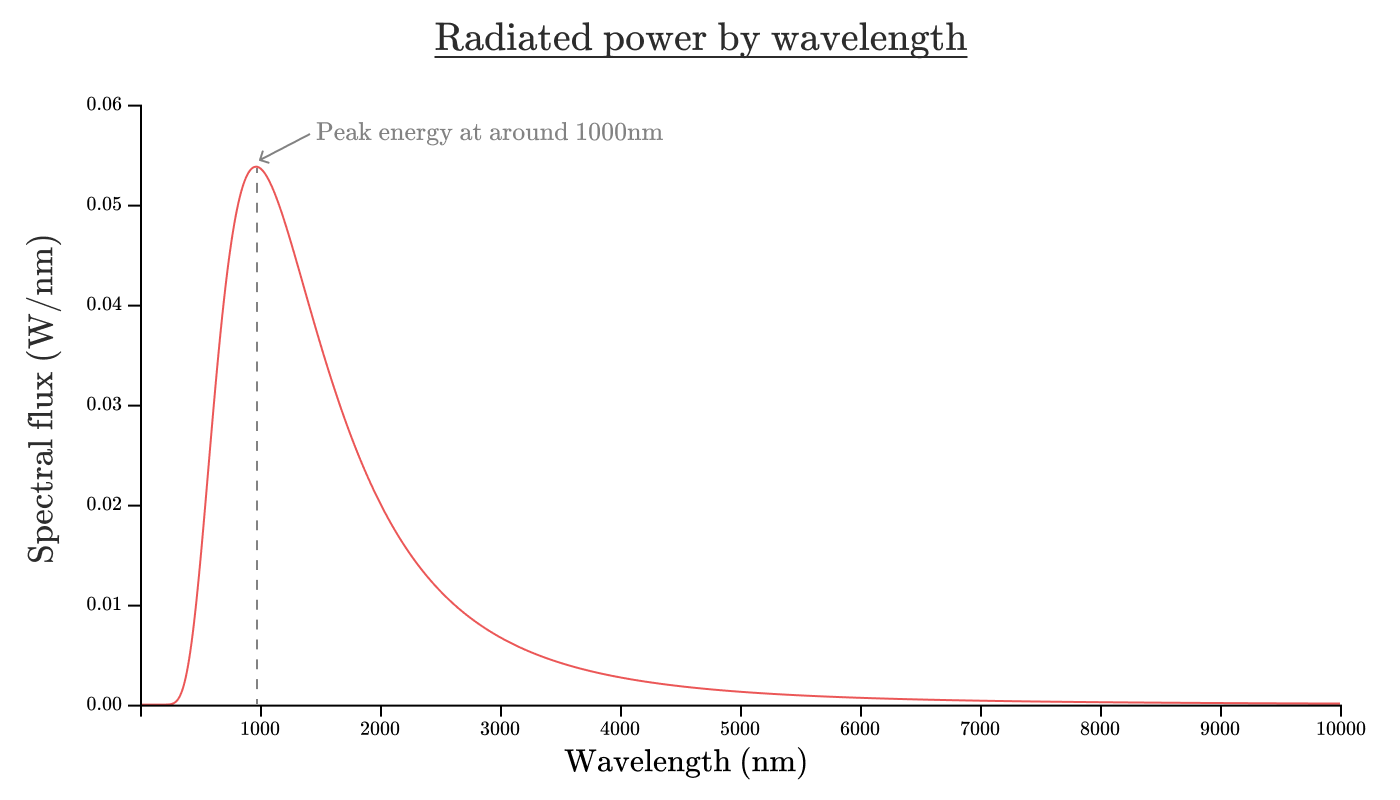
注釈：
波長に対する放射エネルギー
波長1000nm付近でピークエネルギーが得られる
分光放射束（W/nm)
波長（nm）

この曲線の下側の面積が放射束となります。式で表すと、 Φ e = ∫ 0 ∞ Φ e , λ ( λ ) d λ となります。この場合、曲線の下側の面積は、約80Wです。

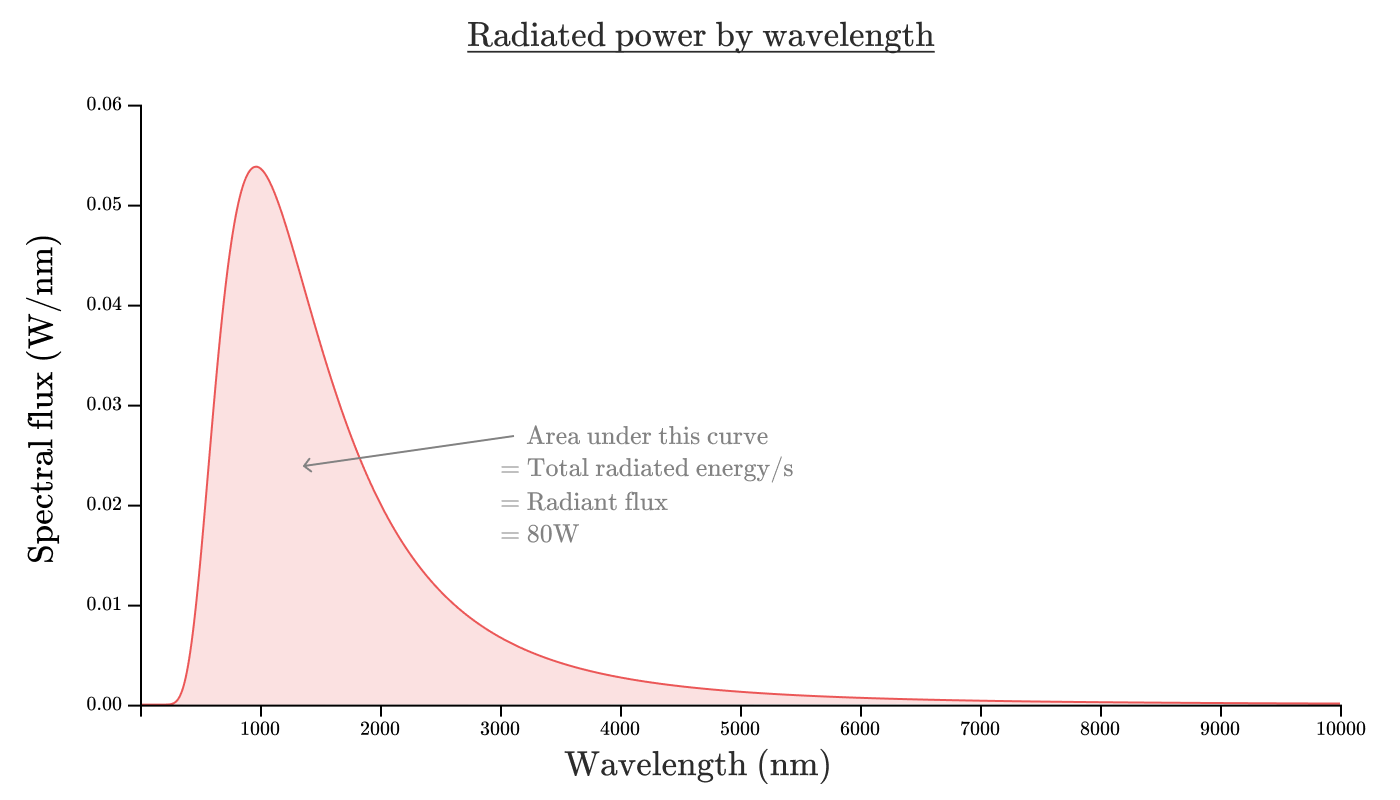
注釈：
波長に対する放射エネルギー
曲線の下側の面積
＝合計放射エネルギー/秒
＝放射束
＝80W
分光放射束（W/nm)
波長（nm）

Φ e bulb = ∫ 0 ∞ Φ e , λ bulb ( λ ) d λ = 8 0 W

「地球に優しい運動」などで、白熱電球は恐ろしく効率が悪いという話を聞いたことがあっても、これを見ると、「80％なら悪くない」という気がするかもしれません。

それは本当です。白熱球は、電気を放射エネルギーに変換するための、かなり効率の良い方法です。でも、残念ながら、電気を 人間の目に見える 放射線に変換するための方法としては、悲惨です。

可視光線

可視光線は、λ=380nmからλ=750nmまでの波長範囲の電磁放射です。この例の白熱電球のグラフでは、下の図の色付きの領域です。

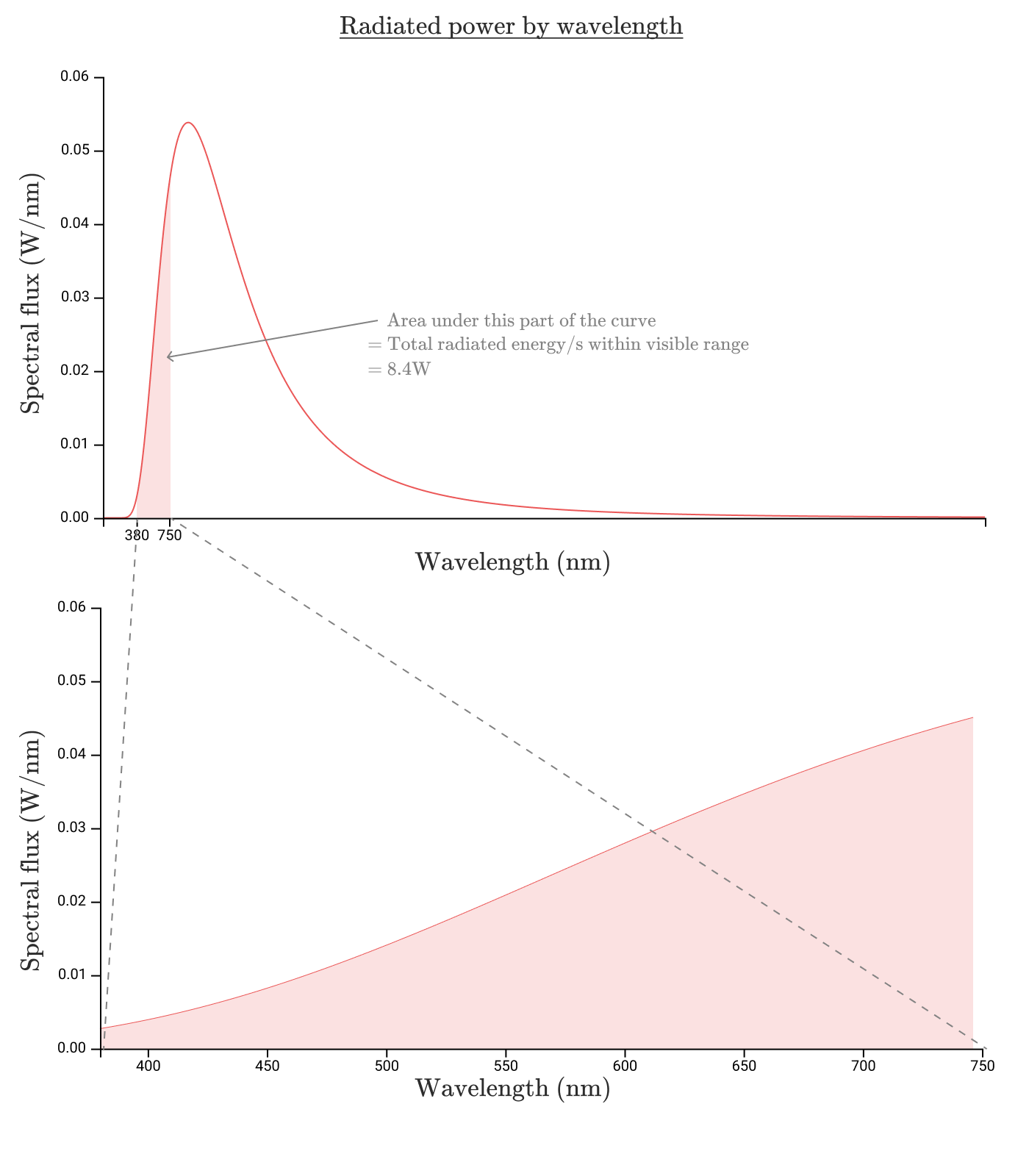
注釈：
波長に対する放射エネルギー
曲線の下側の面積
＝可視範囲内の合計放射エネルギー/秒
＝8.4W
分光放射束（W/nm)
波長（nm）

∫ 3 8 0 nm 7 5 0 nm Φ e , λ bulb ( λ ) d λ = 8 . 7 W

つまり、 可視スペクトル内 で放射されるエネルギーは8.7Wで、効率は8.7%です。かなり酷いように見えます。でも、実は、もっと効率が悪いのです。

その理由を知るために、なぜ可視光線が 目に見える のか考えてみましょう。

人間が知覚する輝度

写真： Christopher Burns

白熱電球の放射が全ての波長で等しいわけではないのと同じように、私たちの目も、全ての波長の放射に対して感受性が等しいわけではありません。全ての波長について人間の目の感受性を測定すると、 比視感度関数 が得られます。標準比視感度関数yˉ(λ)は、次のような形です。

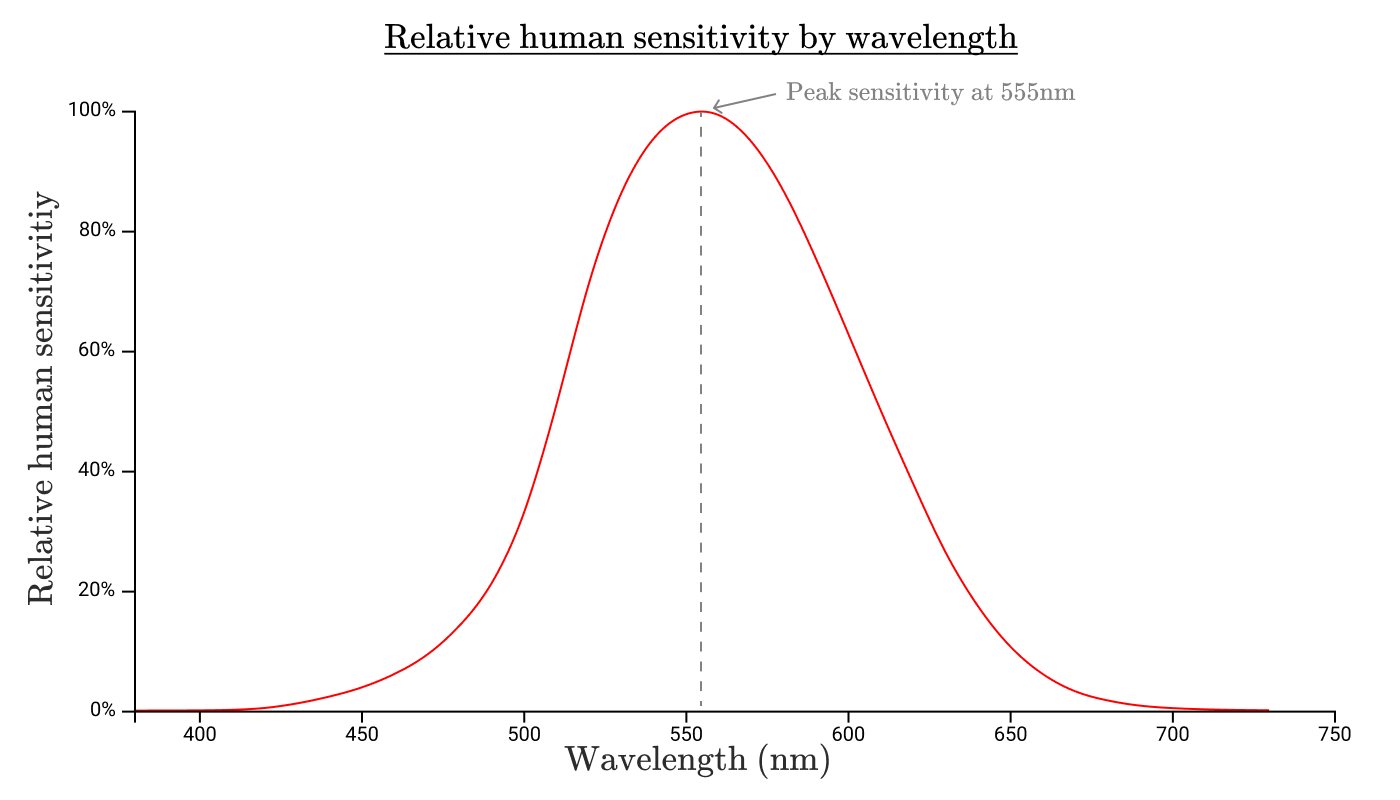
注釈：
波長に対する人間の比視感度
波長555nmでピーク感度が得られる
人間の比視感度
波長（nm）

この比視感度関数の境界によって、可視光線の範囲が 定まります 。この範囲の外にあるものは目に見えません。なぜなら、人間の目には、それに対する感受性がないからです。

さらに、この曲線から、人間の目の感受性が、650nmまたは450nmの波長の放射よりも550nmの波長の放射に対しての方が ずっと 高いことがわかります。

他の動物の目は、これとは異なる波長範囲に対して感受性が高く、したがって、比視感度関数も異なります。鳥にはλ=300nmからλ=400nmの範囲の紫外線が見えるので、もしも鳥の学者が電磁スペクトルを定義したなら、この範囲は「可視光線」の一部になっていたでしょう。

写真： Timothy Rhyne

分光放射束のグラフに比視感度関数yˉ(λ)を乗算することによって、ある光源から放出された波長のそれぞれについて、人間に知覚される輝度への寄与を表す関数が得られます。

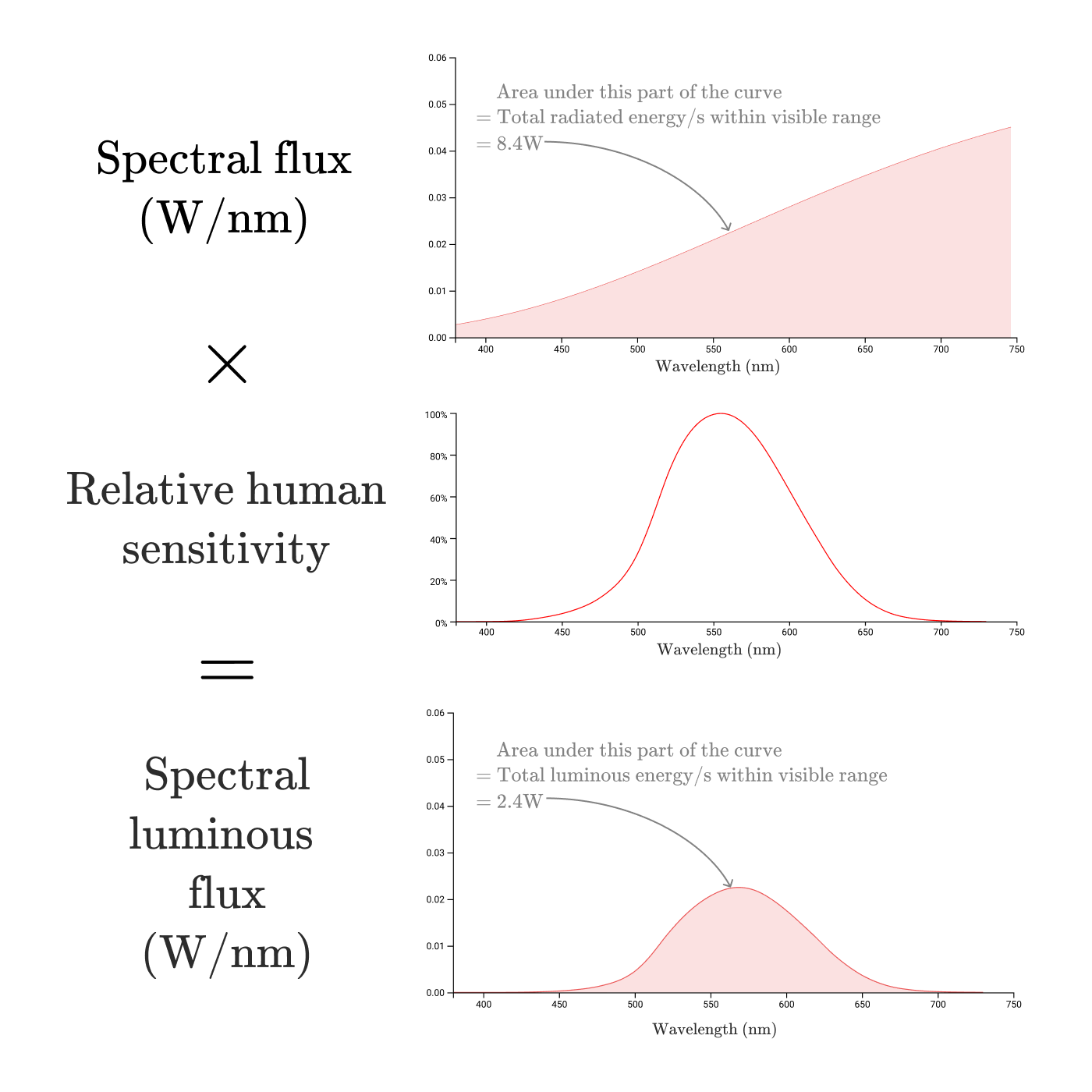
*注釈：
分光放射束（W/nm）
曲線の下側の面積
＝可視範囲内の合計放射エネルギー/秒
＝8.4W
波長（nm）

人間の比視感度
波長（nm）

分光比視感度束（W/nm）
曲線の下側の面積
＝可視範囲内の合計比視感度エネルギー/秒
＝2.4W
波長（nm）*

これが 分光比視感度束 （Φv,λ）です。これが客観的なエネルギーではなく人間の知覚に関するものであることを確認するために、比視感度束は通常、ワットではなくルーメンで測られます。変換比は683.002lm/Wです。

Φ v , λ ( λ ) = 6 8 3 . 0 0 2 W lm ⋅ y ˉ ( λ ) ⋅ Φ e , λ ( λ )

ある光源の 比視感度束 （ Φ v ）は、その光の 人間が知覚した エネルギーの合計です。

分光放射束曲線の下の面積によって放射束を計算したのと同様に、比視感度束は、分光 比視感度 束曲線の下の面積と、知覚されるワット数からルーメンへの定数変換によって得られます。

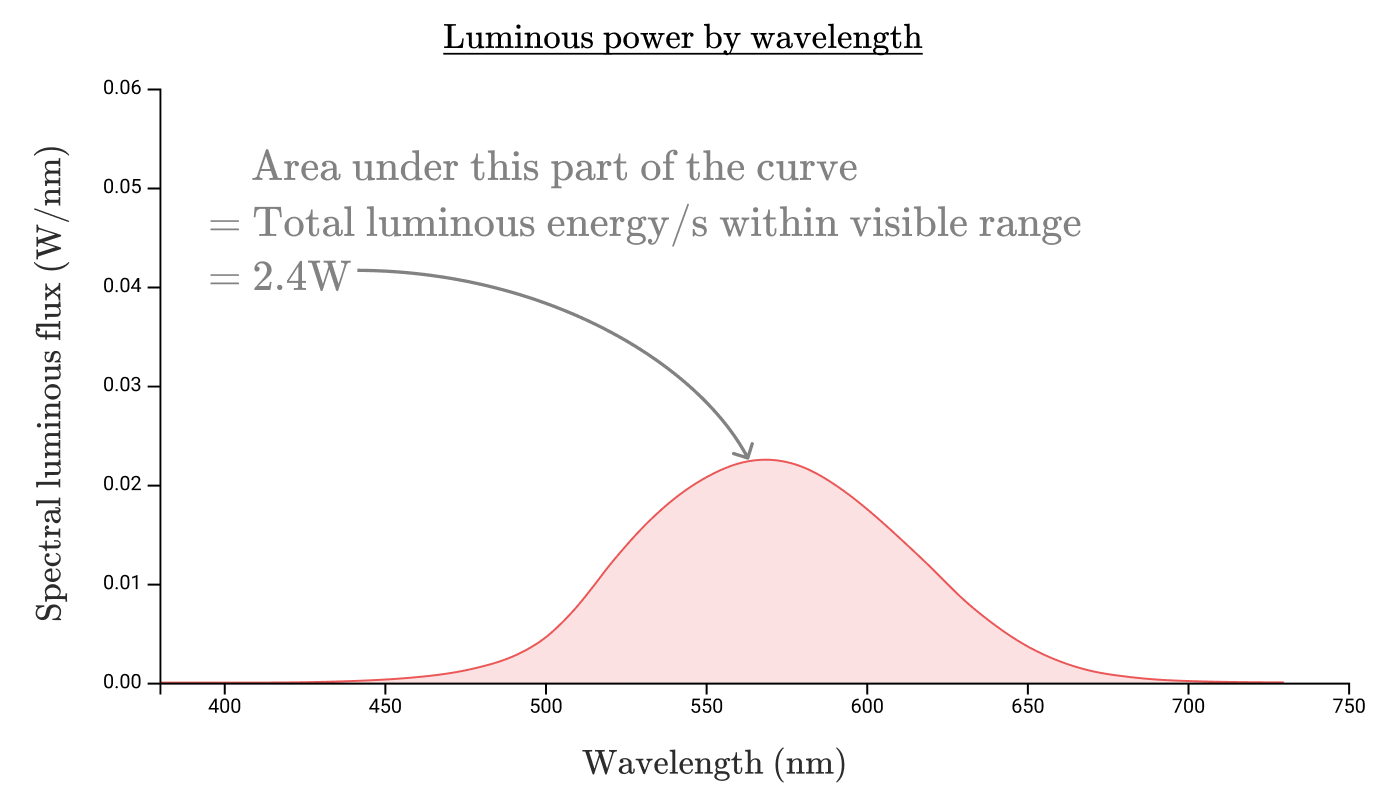
注釈：
波長に対する比視感度エネルギー
分光比視感度束（W/nm）
曲線の下側の面積
＝可視範囲内の合計比視感度エネルギー/秒
＝2.4W
分光比視感度束
波長（nm）

Φ v bulb = ∫ 0 ∞ y ˉ ( λ ) ⋅ Φ e , λ bulb ( λ ) d λ = 6 8 3 . 0 0 2 W lm ⋅ 2 . 4 W ≈ 1 6 0 0 lm

よって、この例の100Wの白熱電球の比視感度束は、わずか2.4W、つまり1600lmです。この電球の発光効率は2.4%で、電気を放射に変換する効率の80%にはほど遠いものです。

仮に放射されたものが可視範囲に集中するような光源があれば、それはより効率的な照明になるはずです。ここで、白熱電球、蛍光灯、LED電球のスペクトルを比較してみましょう。

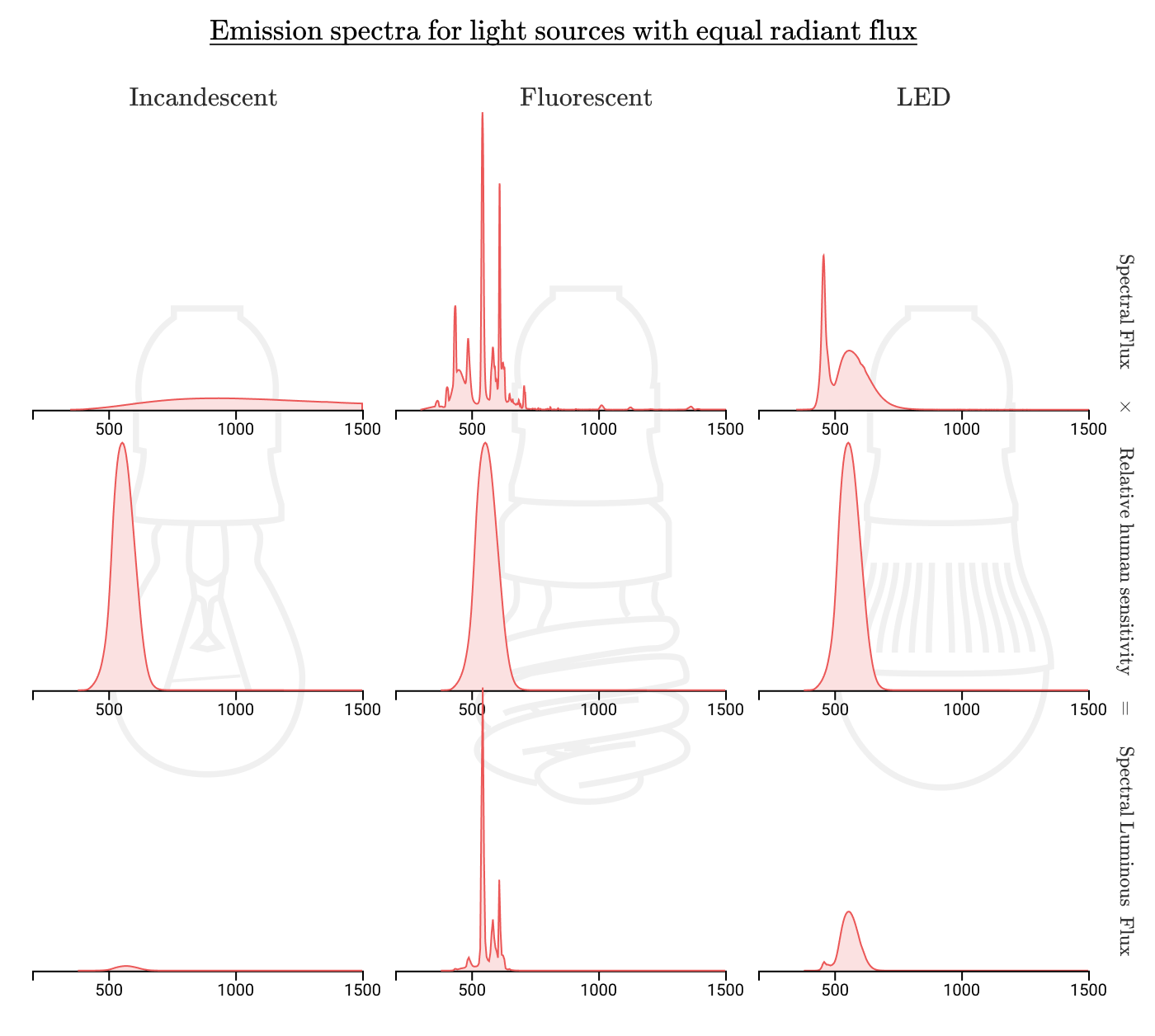
注釈：
放射束が等しい光源の発光スペクトル
白熱電球
蛍光灯
LED
分光放射束
人間の比視感度
分光比視感度束

図を見ると、蛍光灯やLED電球では、人間に見えない波長における放射エネルギーの無駄がはるかに少ないことが分かるでしょう。1～3％と低い白熱電球の効率に対して、蛍光灯の効率は約10％、LED電球の効率は20％にも達します。

さて、輝度の説明はこれで終わりです。再び話を本題に戻し、色を見ていきましょう。

色の定量化

写真： Lauren Mancke

私たちは、色をどのように特定しているのでしょうか。例えば目の前にレモンがあるとしましょう。その色を電話越しに説明する場合、どうやって相手に伝えたらいいと思いますか。”レモンは黄色だよ”と言えばいいじゃないか、と思われるかもしれません。でも、どういった黄色ですか。どうやったら、それぞれの黄色を正確に説明できるのでしょうか。

電磁放射を人間が解釈したものが色だという知識をベースに、分光放射束を介して、色を数学的に定義付けできるかもしれません。人間が視認できる色は、単色（単一波長）の重み付けされた組み合わせです。なお、単色は、スペクトル色とも言われています。

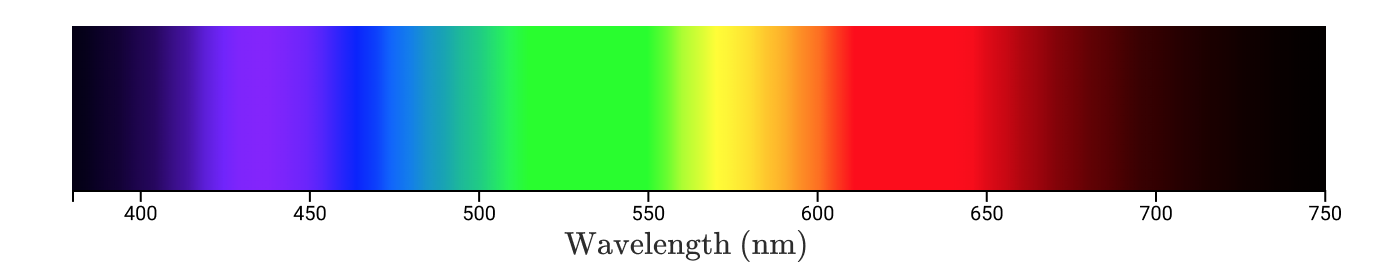
注釈：
波長（nm）

波長による単色の分類

どのような物体に対しても、その放射（または反射）スペクトルを測定し、それを使って正確に色を識別することができます。つまりスペクトルを再現できれば、確実に色を再現できるというわけです。

レモン表面のある一点から反射した太陽光は、恐らく次の図のような反射スペクトルになると思われます。

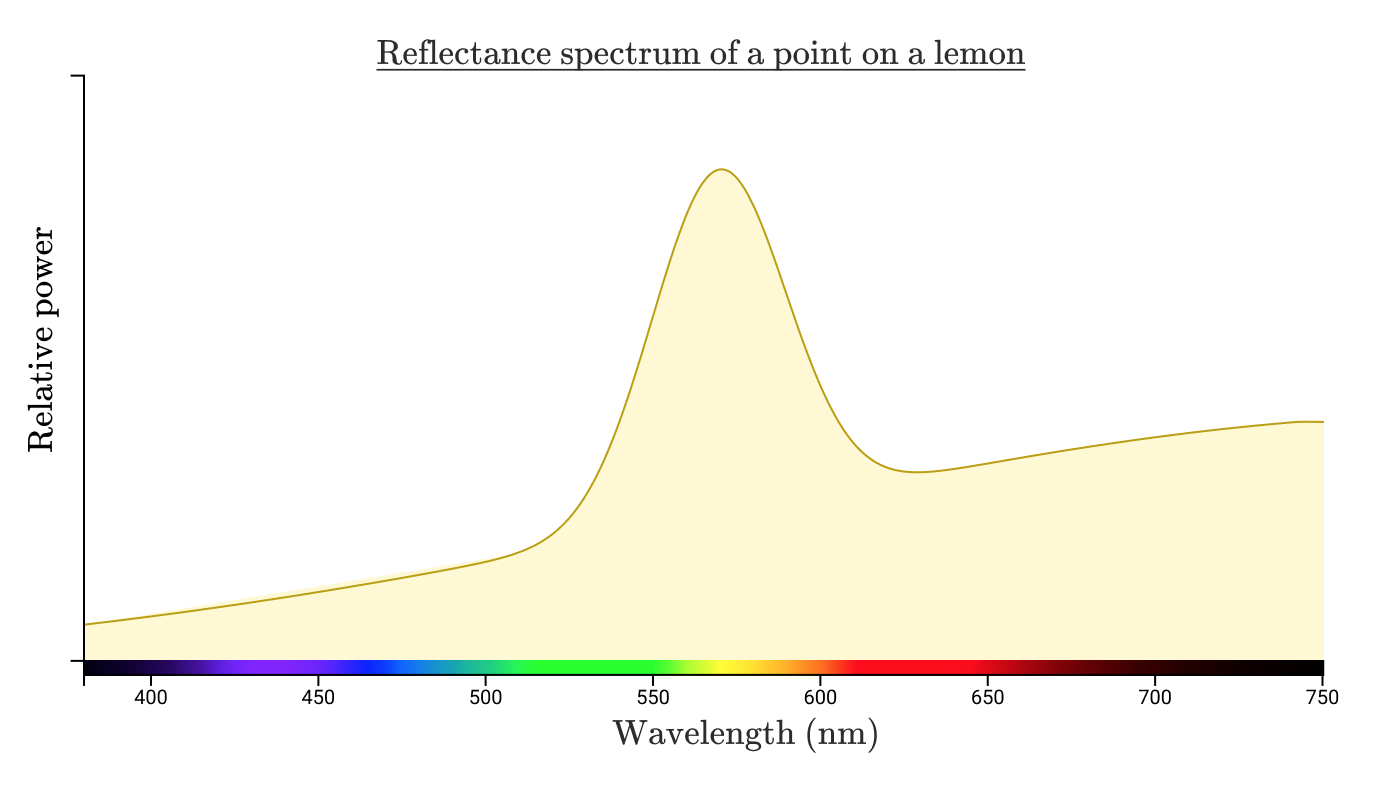
注釈：
レモン表面のある一点からの反射スペクトル
強度比
波長（nm）

注：目に到達する放射エネルギーの強度とスペクトル分布は、光源の強度と発光スペクトル、光源と照らされた物体との距離、物体のサイズと形状、物体の吸収スペクトル、およびそれを見る人と物体との距離に依存します。このように考慮すべき事項が多いため、ここでは光が目に到達した時に何が起こるかについてのみ焦点を当てたいと思います。また、概念の理解に集中するために、ここでは単位については考えません。

このスペクトル分布を持つエネルギーが目に到達すると、私たちはそれを”黄色”と認識します。例えば、レモンの写真を撮って、コンピュータにアップロードするとしましょう。その後、画面上のレモンの特定部分の色と、実際のレモンの特定部分の色の違いが、ほとんど知覚できない程度にまで注意深く色調整するとします。

ここで画面の分光分布を測定した場合、どのような分布になると思いますか。当たり前に考えると、上記のレモンの反射スペクトルと似通ったものになるはずです。しかし、実際は以下の図のようになります。

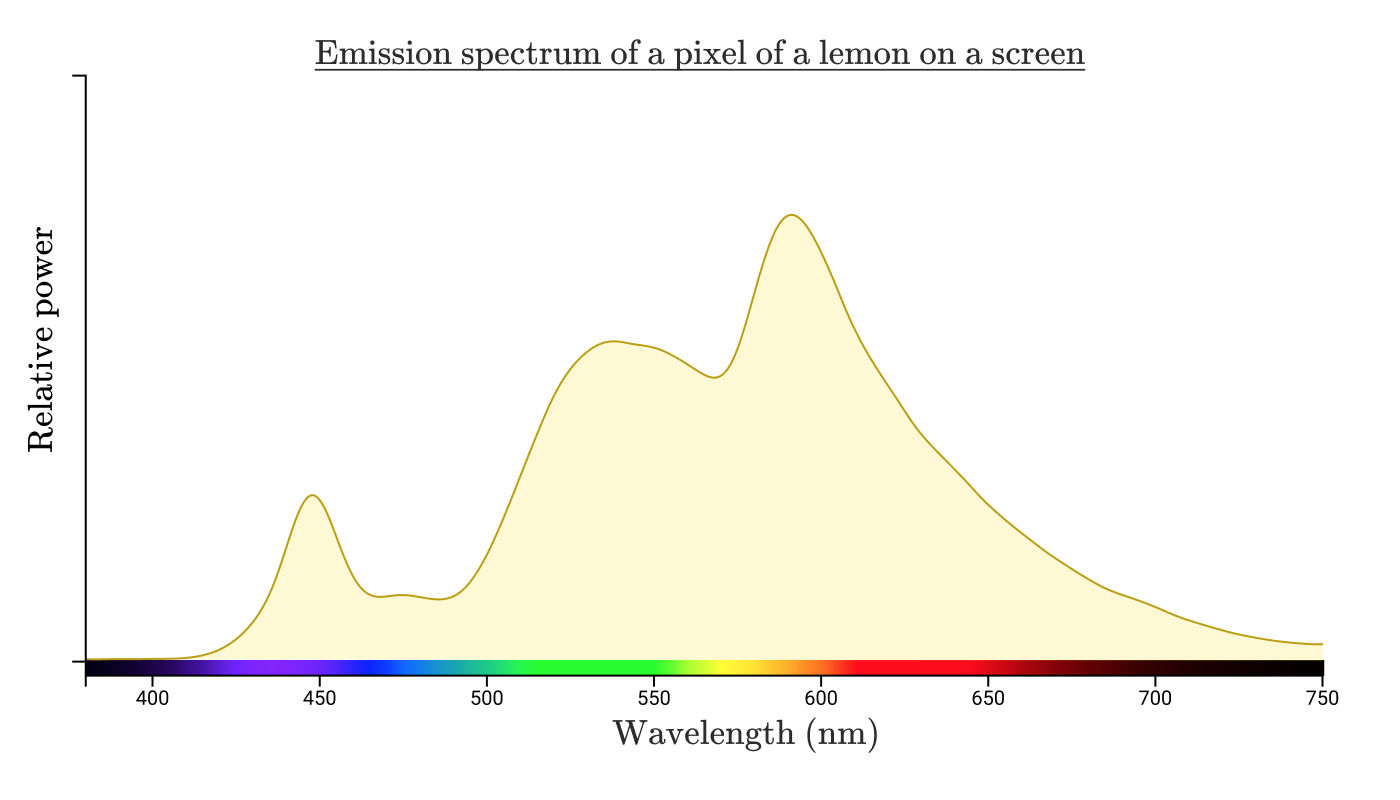
注釈：
画面に表示されたレモンのピクセルの発光スペクトル
強度比
波長（nm）

人間にとって同じように見える2つの異なる分光分布は、 メタマー と呼ばれています。

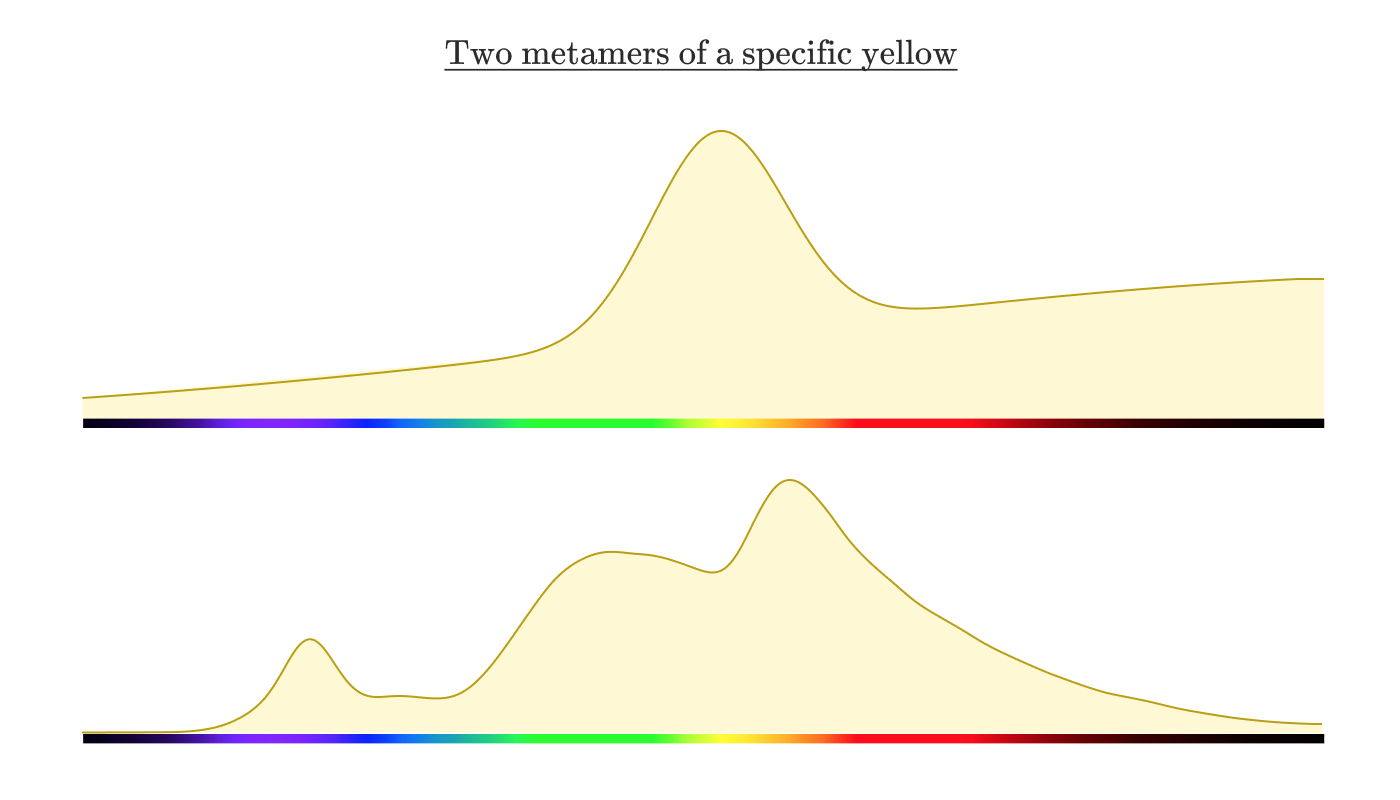
注釈：
特定の黄色の2つのメタマー

この仕組みを理解するため、目の生物学的な側面について見ていきましょう。

視覚の生物学的メカニズム

写真： Amanda Dalbjörn

光の知覚は、目の”桿体細胞”と”錐体細胞”という特殊細胞で行われます。桿体細胞は、主に低照度環境で重要な役割を担っており、色覚ではあまり重要な役割を果たさないため、ここでは錐体細胞に焦点を当てます。

人間には通常3種類の錐体が備わっており、3つの異なる錐体を持つ状態を”3色型色覚”と言います。ただし、少なくとも1つの事例で 4色型色覚の人間 も確認されています。また、他の動物については、例えば16種類の錐体を持つ シャコ類 のように、さらに多くの錐体を持つ種もいます。

それぞれの錐体は、それが励起する光の波長範囲別に名前が付けられており、一般的には”S”、”M”、”L”（short：短、medium：中、long：長）に分けられます。

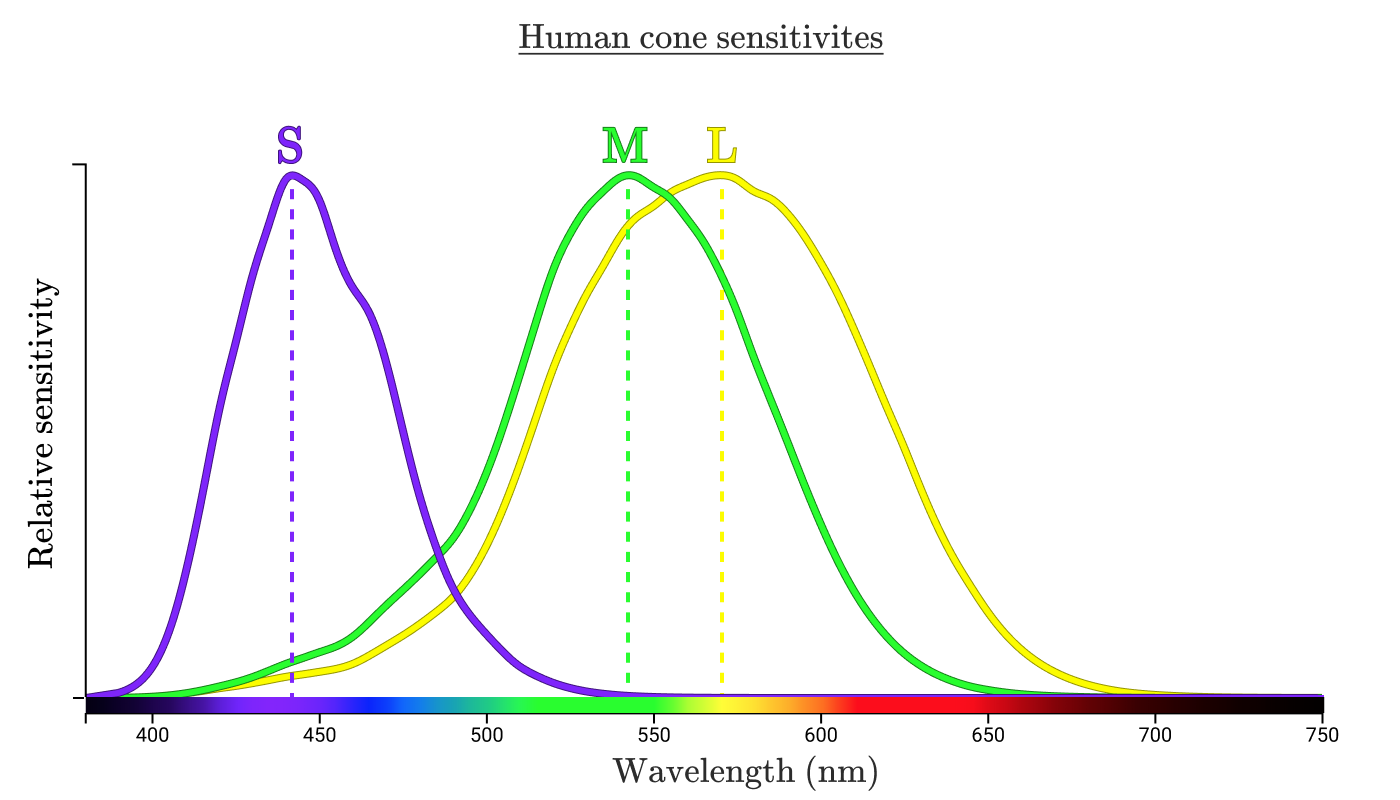
注釈：
人間の錐体感度
相対感度
波長（nm）

上記の3つの曲線が示しているのは、各波長に対する3種類の錐体の感度です。それぞれの曲線の最高点は”ピーク波長”と呼ばれ、錐体の感度が最も高くなる放射エネルギーの波長を示しています。

では、レモンから反射してくる光を、この錐体がどのように処理しているのかを見てみましょう。

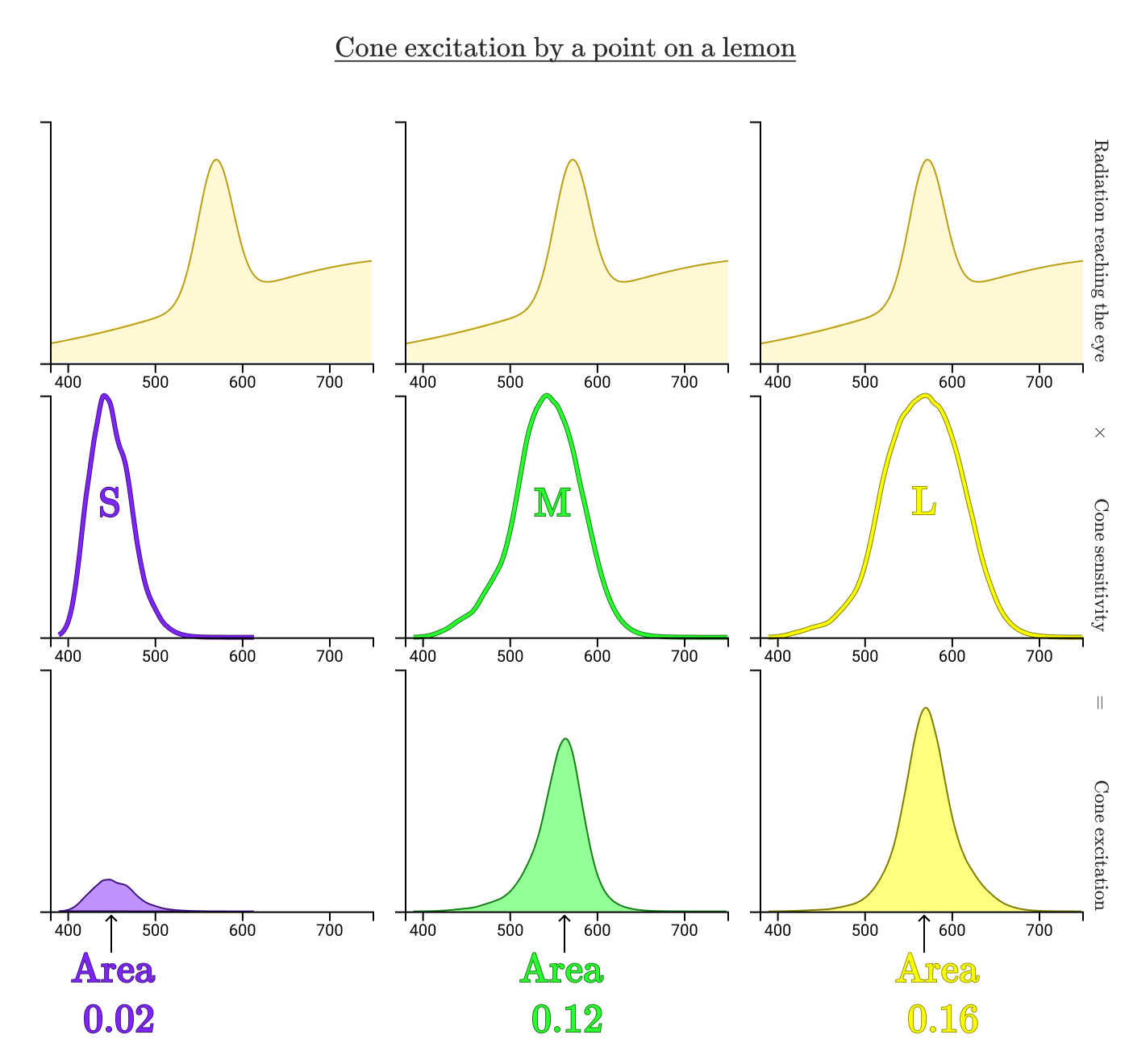
注釈：
レモンのある一点からの錐体の励起
目に到達する放射エネルギー
錐体の感度
錐体の励起
面積

曲線下の正規化された面積を見ると、実際のレモンから反射された放射エネルギーが、各錐体をどの程度励起させているかが分かります。上記の場合、S、M、Lの錐体の正規化された励起はそれぞれ0.02、0.12、0.16です。では次に、画面上のレモンの場合について見てみましょう。

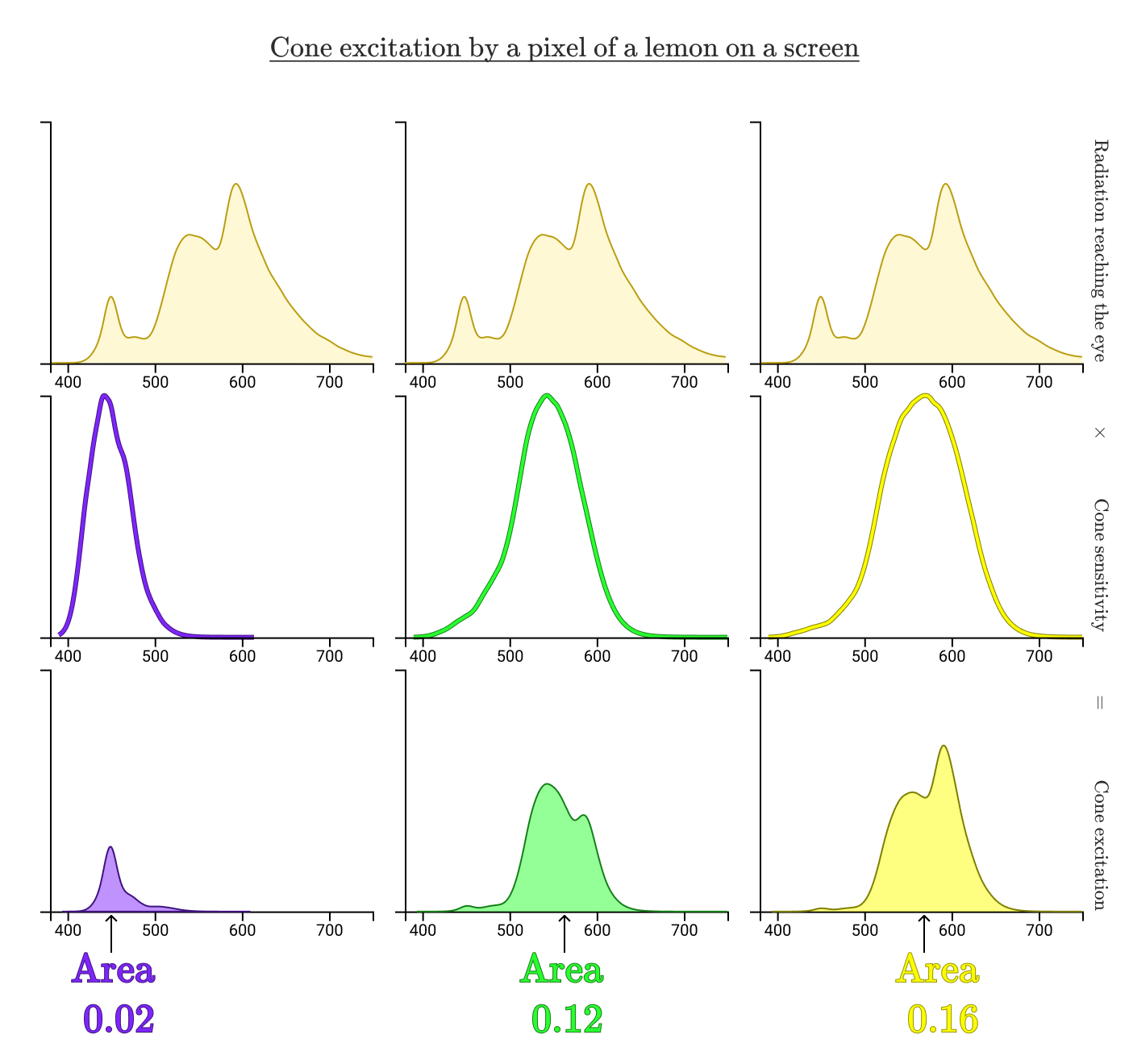
注釈：
画面上のレモンのあるピクセルからの錐体の励起
目に到達する放射エネルギー
錐体の感度
錐体の励起
面積

目に届く放射スペクトルは全く違うにもかかわらず、錐体の 励振 は同じです（S=0.02、M=0.12、L=0.16）。だからこそ、実際のレモンのある一点とデジタル表示されたレモンのある一点は同じように見えたのです。

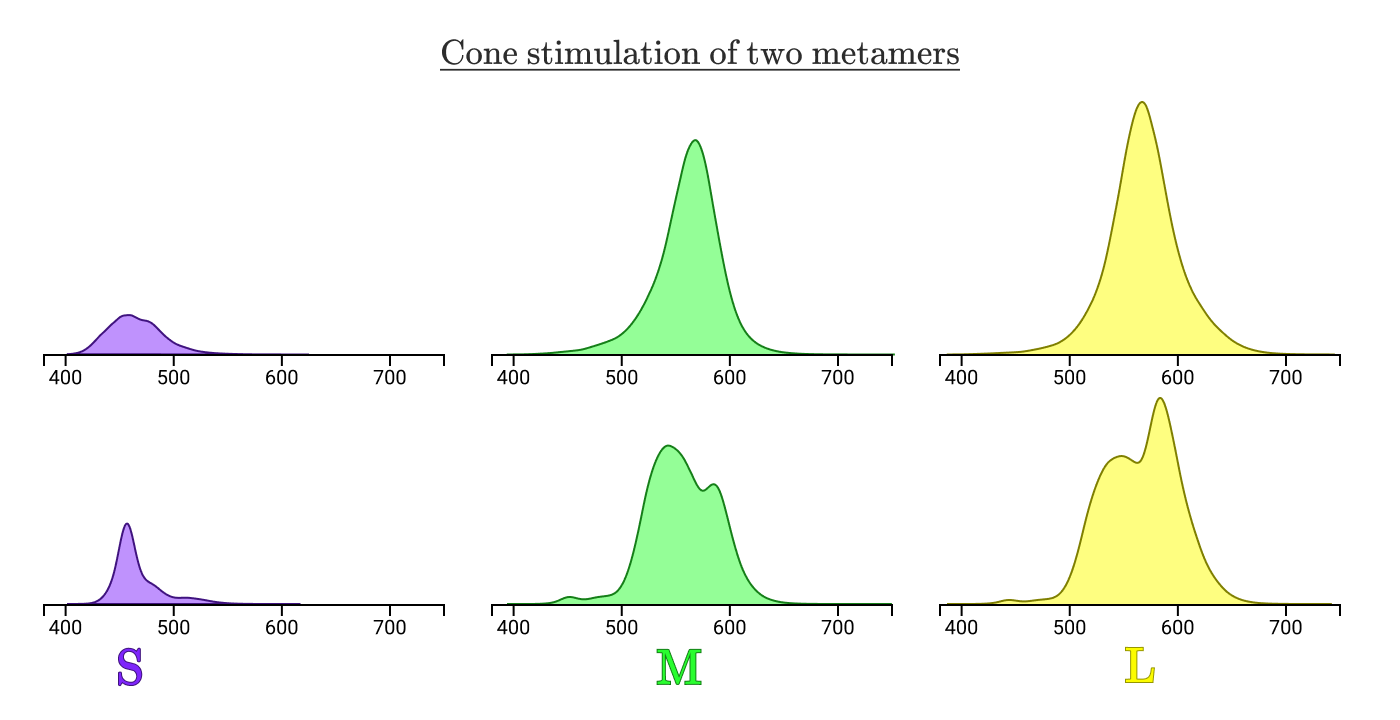
注釈：
2つのメタマーの錐体の刺激

メタマーの場合、刺激曲線の下の正規化された錐体の面積は3つの錐体の全てにおいて常に等しい。

3組の錐体により分光放射束曲線Φe(λ)が3つの数字（ S、M、L ）に変換され、変換されたトリプレット（ S、M、L ）のそれぞれが個別の色を表します。これは非常に便利と言えるでしょう。なぜなら変換されたトリプレット（0.02、0.12、0.16）は、複雑な連続関数よりもはるかに伝えるのが簡単だからです。数学的に説明すると、私たちの目は無限次元の空間から3次元の空間に次元縮小を行っていると言えます。無意識のうちにこれができるなんて、本当にすごいことですよね。

このトリプレット（ S、M、L ）は、 色空間 の最初の実例でもあります。