色空間

色は、色空間を用いると数値を使って正確に定義できます。前のセクションでは、ある種の黄色がSML色空間で(0.02, 0.12, 0.16)と表せることを見ました。なお、SML色空間は LMS色空間 という名前のほうがよく知られています。

この色空間は、錐体細胞への刺激を表しています。それゆえ、定義づけによって人間が目で捉えられる全ての色を、LMS色空間上で正の値の座標として表すことができます（非常にまれな存在である4色型色覚の人間は除きます。3つの座標ではなく4つの座標が必要になるからです）。

しかし、ああ、SML色空間には不便な特性があります。

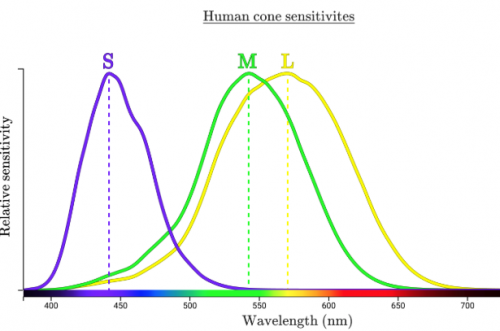
その1つは、全てのトリプレット値（ 三刺激値 とも呼ばれます）が 物理的に実現可能 というわけではないということです。LMS色空間の(0, 1, 0)を考えてみましょう。この座標を物理的に実現するにはLやSの錐体細胞を 全く 刺激せず、Mの錐体細胞のみを刺激する方法を見いださなければなりません。というのも、Mの錐体細胞の感度を表す曲線が全ての波長で少なくともLまたはSのどちらかの錐体細胞の曲線と重なるからです。これでは無理です！

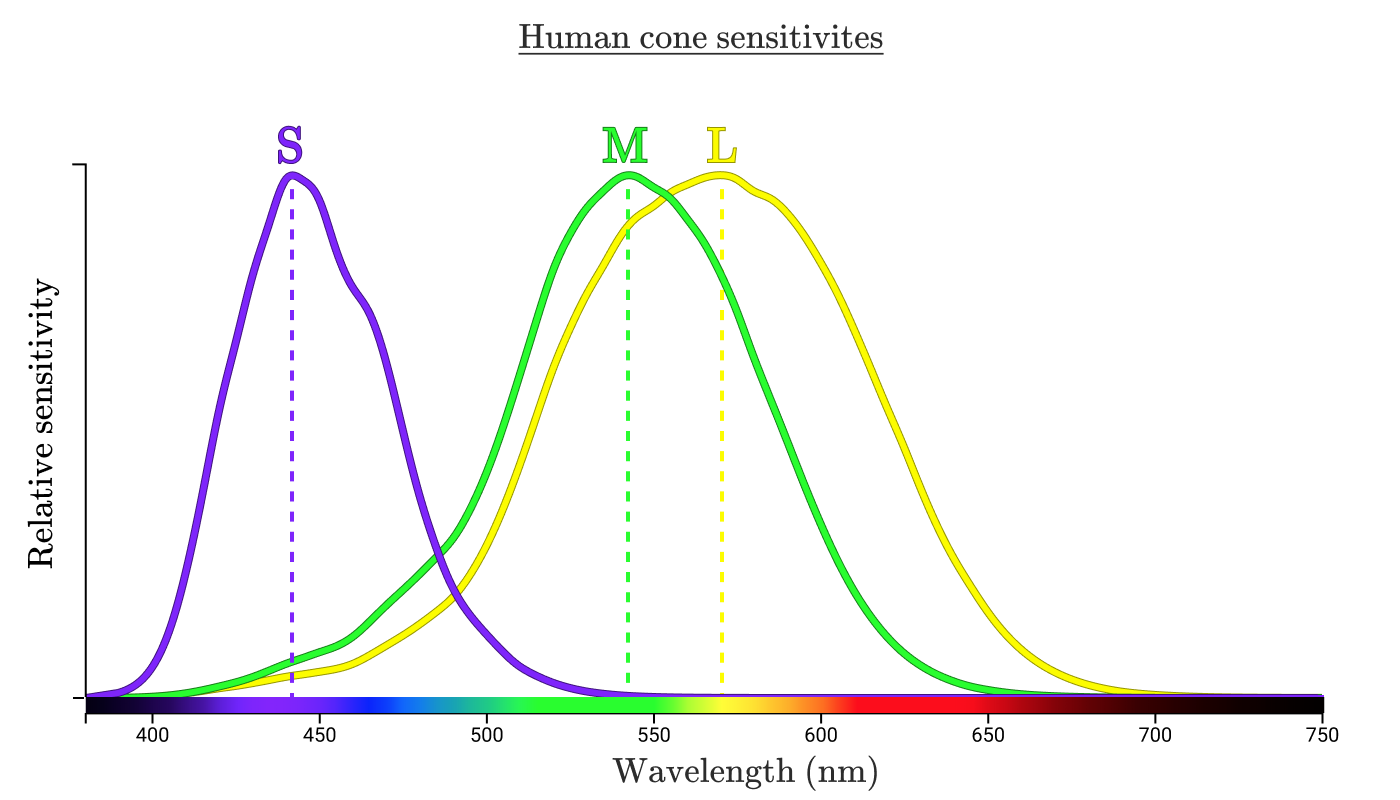
注釈: （タイトル）人間の錐体感度
（縦軸）感度（相対値）
（横軸）波長（nm）

Mの錐体細胞を刺激する波長はLかS（あるいはその双方）の錐体細胞も刺激します。

この事実から引き起こされる問題は、1つの錐体細胞のみに強い刺激を与えるのは非常に難しいということです。つまり、特に表示用ハードウェアを作る上では、SML色空間を利用することはできないということを意味します。

もう1つ、時系列的な順序がもたらす現実的な問題がありました。それは、錐体細胞の感度が正確に分かるようになったのが1990年代だったということです。つまり、色に関してそれ以前に出来た数学的に厳密なモデルを発展させることが必要でした。最初の注目すべき進歩は1920年代の後半です。

ライトとギルドの等色実験

1920年代の後半にライトとギルドは、光の3つの波長を干渉させて正確に色を定義する実験を指揮しました。

2人は眼球の3種の錐体細胞については知らなかったかもしれません。しかし、目に見えるあらゆる色は3つの色の組み合わせから出来ているという考え方は、少なくとも彼らに先立つこと100年前から提唱されていました。

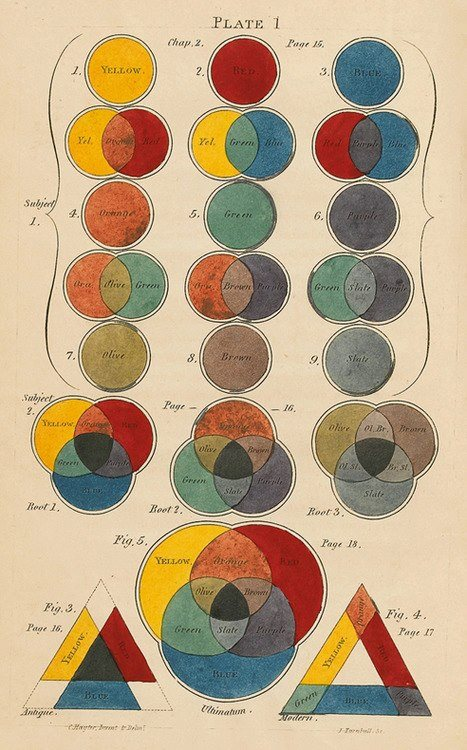
3色の理論の例（Charles Hayter 1826年）

ライトとギルドには、3種の固定された波長を持つ光源を組み合わせることで、被験者が色を再構成できるような仕組みを作るというアイデアがありました。この仕組みは次のようなものです。

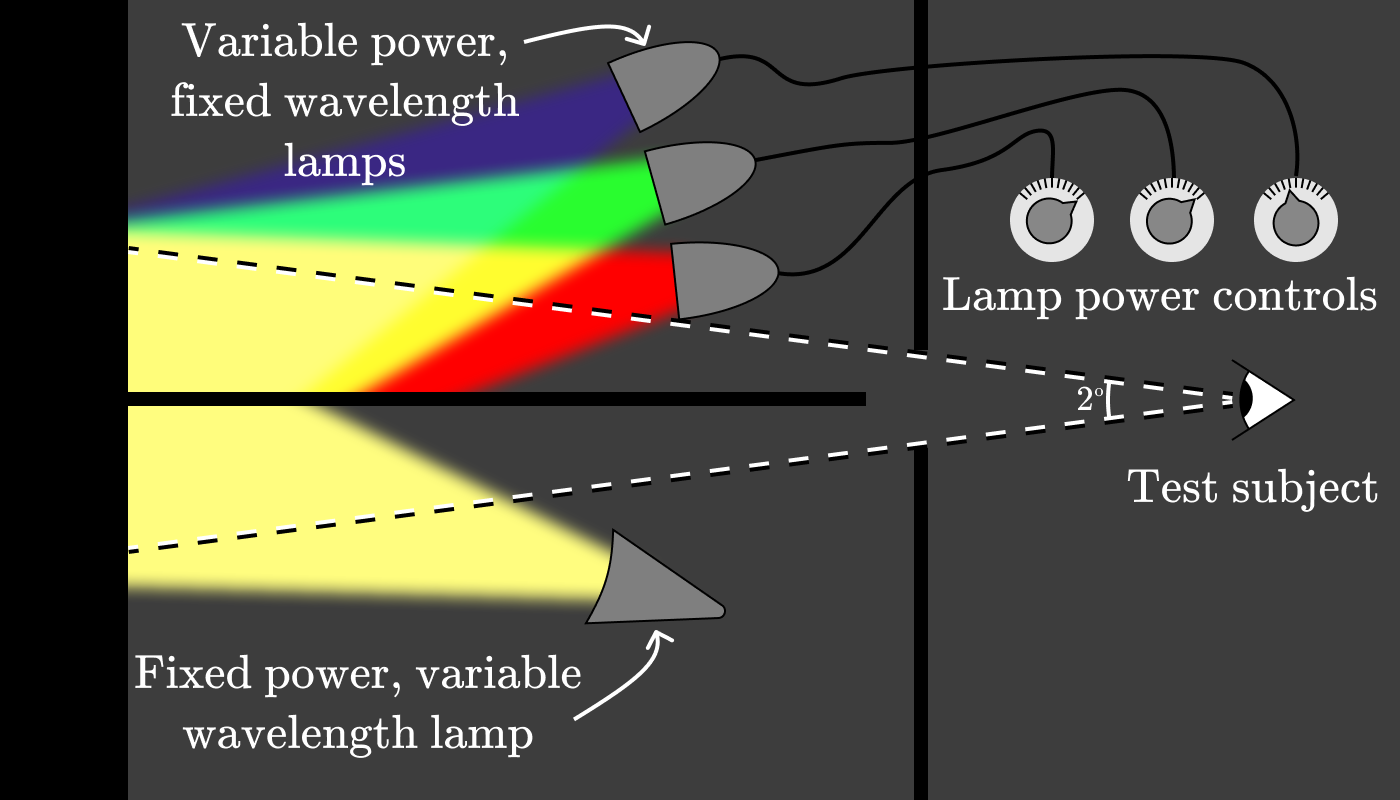
注釈: （左上）変動出力、固定波長の光源
（左下）固定出力、可変波長の光源
（右上）光源の出力調整
（右下）被験者

実験では、まず下側の光源をターゲットの波長に設定します（例えば600nm（以下同じ。）。次に、被験者が見ている色と同じになるように3個の光源の出力の調整するよう依頼します。

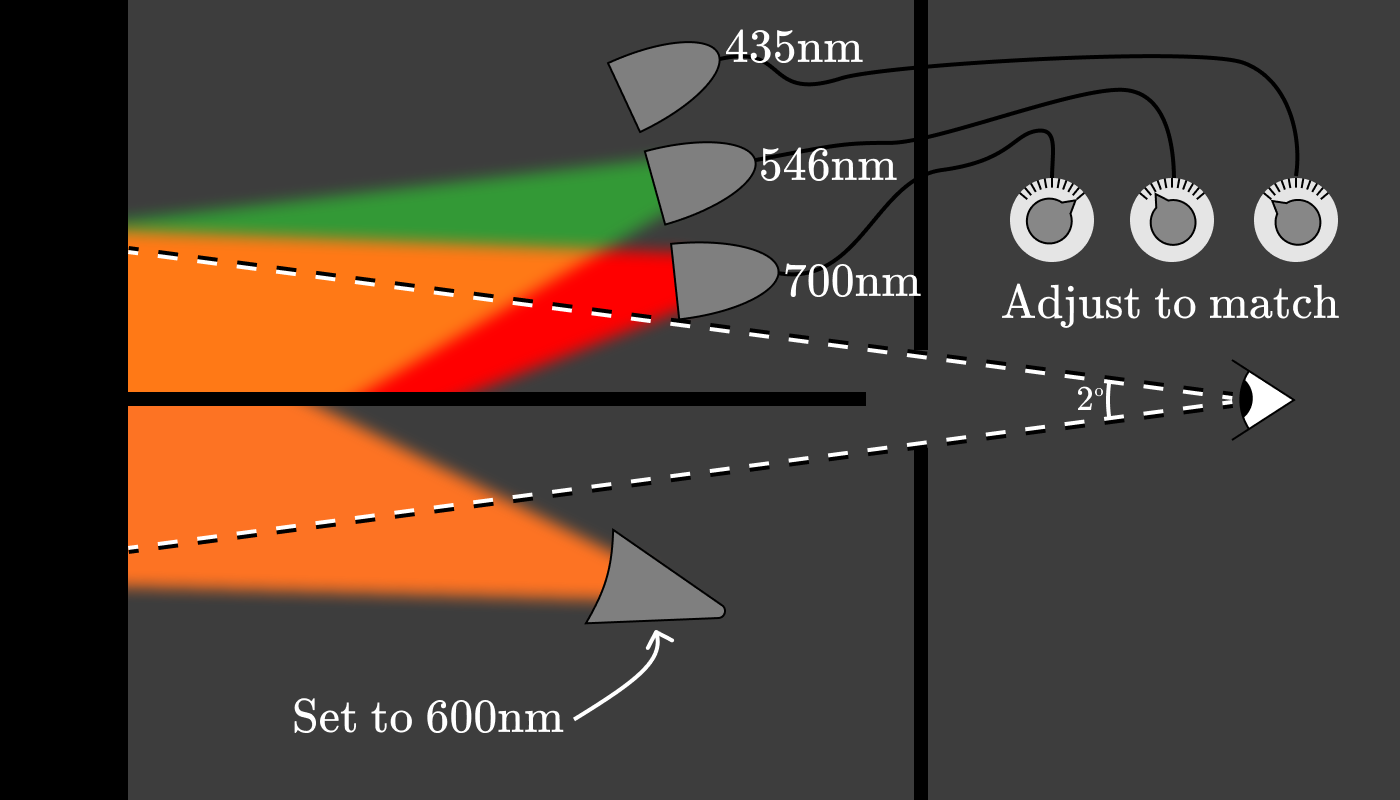
注釈: （左下）600nmにセット
（右）同じになるように調整

3個のツマミを使って出力を設定すると、3色（赤、緑、青）のトリプレット値で600nmの単色光を特定できます。このプロセスを5nmごとに繰り返して10人の被験者に行います。出来上がったグラフは、被験者に提示された波長の色を再現するのに必要な赤（700nm）、緑（546nm）、青（435nm）の光の量を示しています。これは現在、 等色関数（CMFs） として知られています。

等色関数は r ˉ ( λ ) 、 g ˉ ( λ ) 、 b ˉ ( λ ) で表されます。

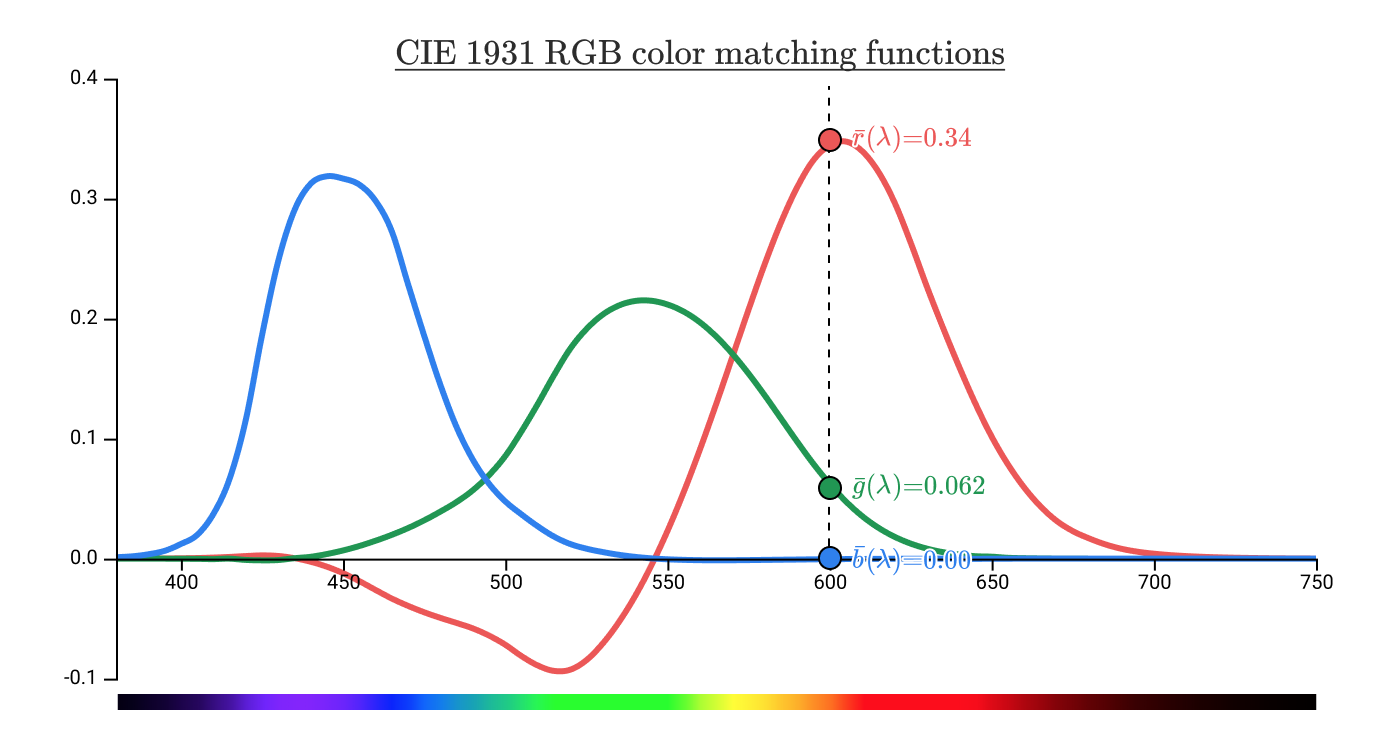
上の図は600nmの単色光が（ R , G , B ）の座標（0.34, 0.062, 0.00）で表せることを示しています。この座標が CIE1931 RGB色空間 の値です。

でも、ちょっと待ってください。次のように関数が負の値になると何を意味するのでしょうか。

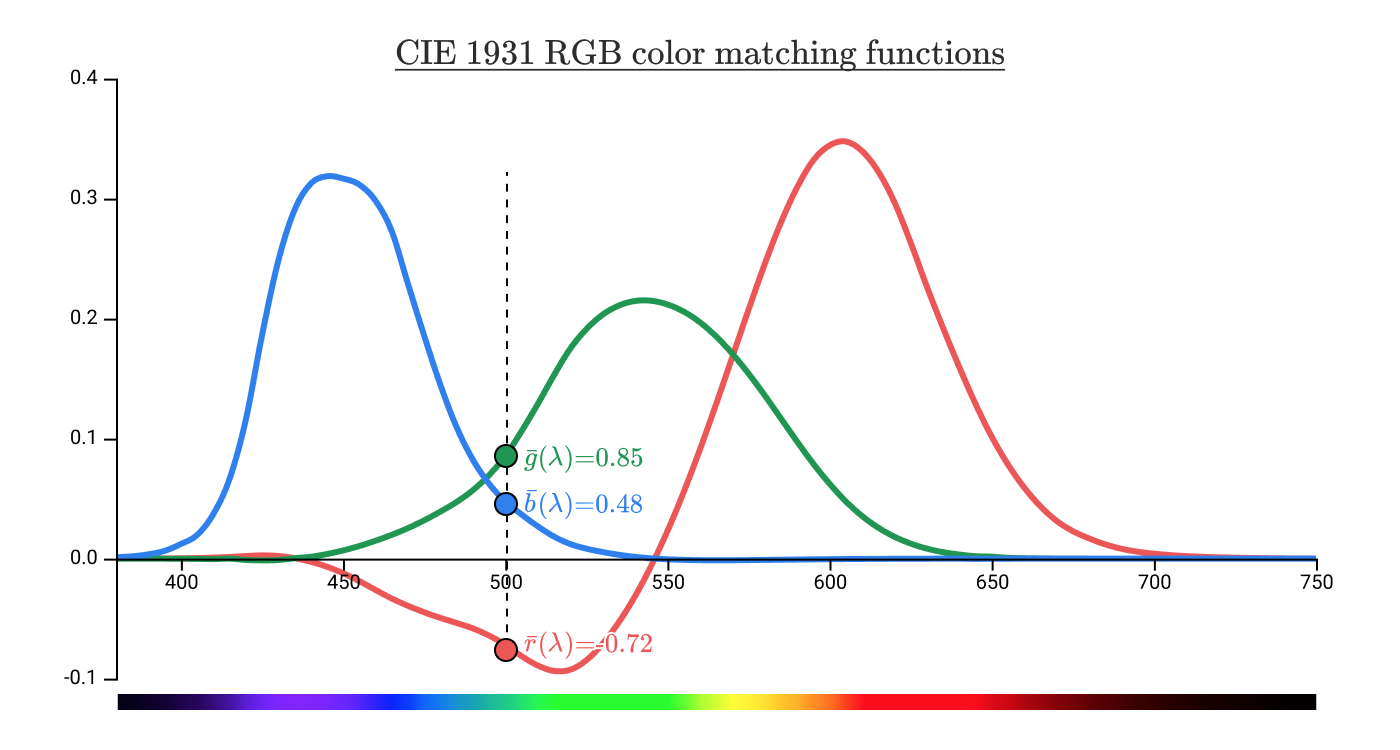
500nmの光源の（ R , G , B ）の座標は(-0.72, 0.85, 0.48)です。一体、-0.72はどういう意味なのでしょうか。

赤（700nm）の出力の値を幾つに設定しても、500nmの光に合わせることができないということが分かっています。この場合、青と緑の値は関係ありません。しかし、赤の光源を 下側へ 追加すると上下の色が一致します。

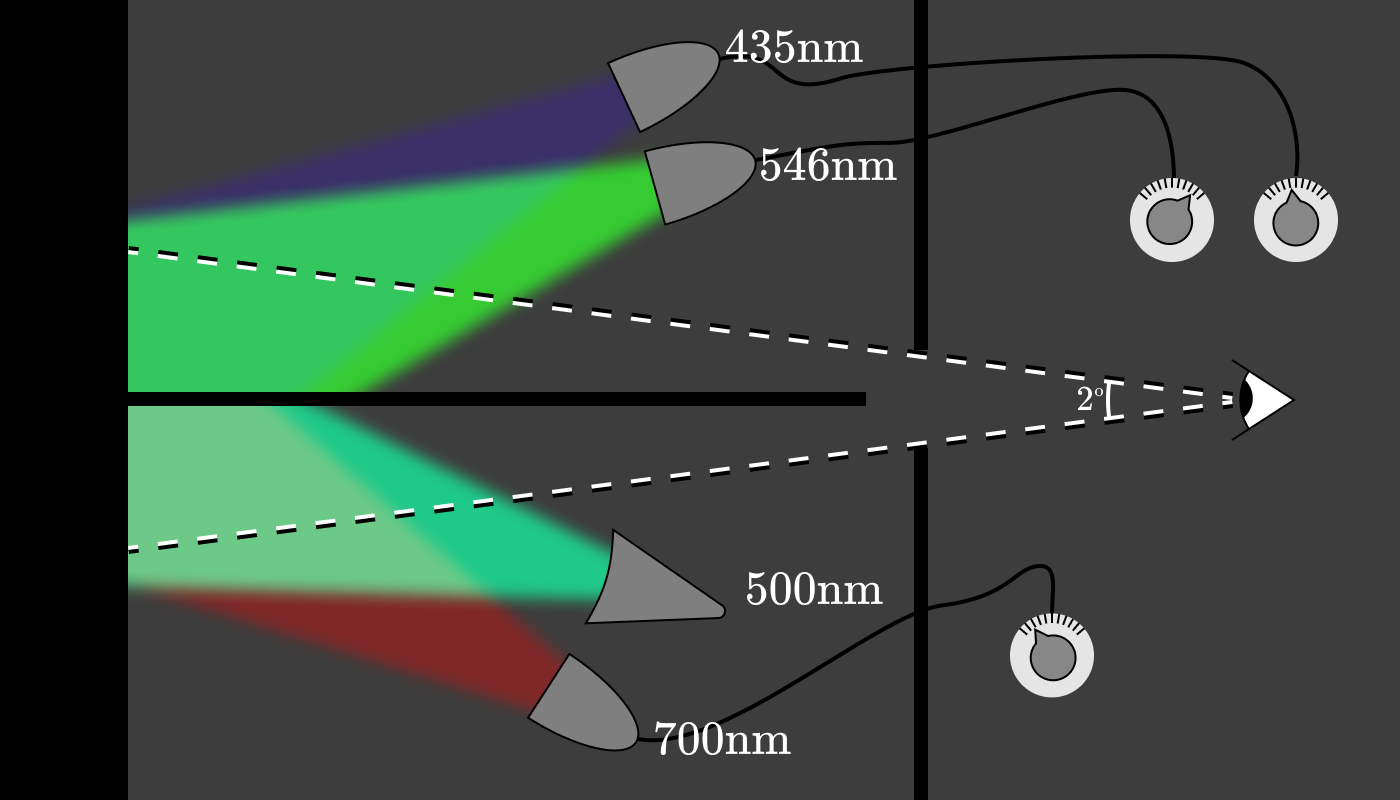
たぶん、実際の実験の装置は両側に3個の可変出力の光源を持てばよかったのでしょう。仕切りの両側に固定波長の光源があれば、どの色の光源も負の値に合わせることができます。

等色関数を見れば、赤（700nm）、緑（546nm）、青（435nm）をどういう比率で組み合わせたらいいか（負の値となる場合もあります）が分かります。これで、あらゆる単色光を再現することができます。

L、M、S錐体細胞の感度関数では、任意のスペクトル分布で、錐体細胞を刺激する値を決定することができましたが、同じことが等色関数でもできます。では、さっきのレモンの色の例に適用してみましょう。

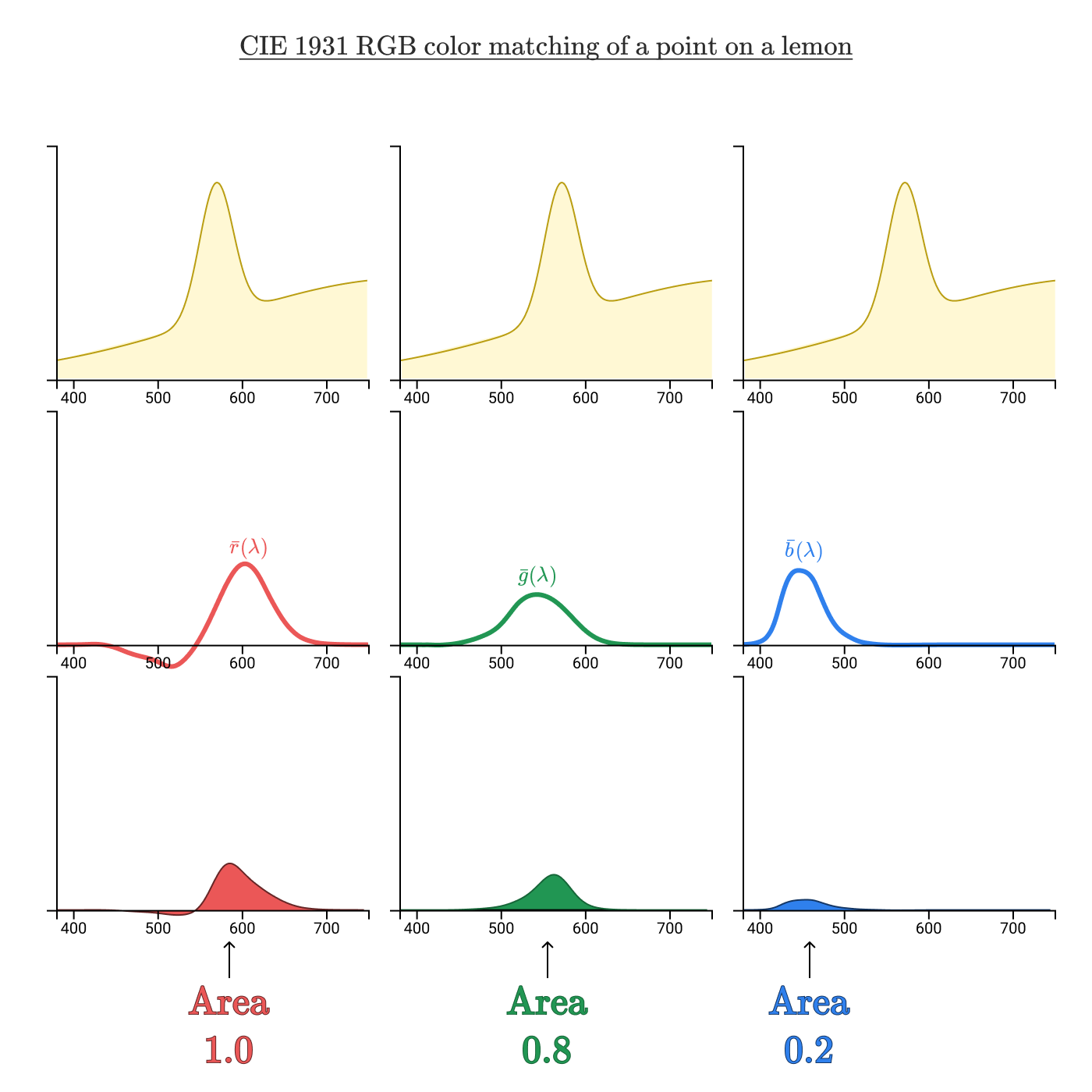
スペクトル曲線と等色関数の掛け算により得られる曲線を積分すると、上の図で色が塗られた面積が得られます。これにより、（ R , G , B ）のトリプレット値（1.0, 0.8, 0.2）が算出され、単一の色を識別することができます。

（ L , M , S ）が示す色空間で正確に色を 識別 できるのに対し、この（ R , G , B ）が示す色空間は正確に色を 再現 できます。しかし、等色関数のところで見てきたように、実際、負の（ R , G , B ）座標での色の再現はできません。

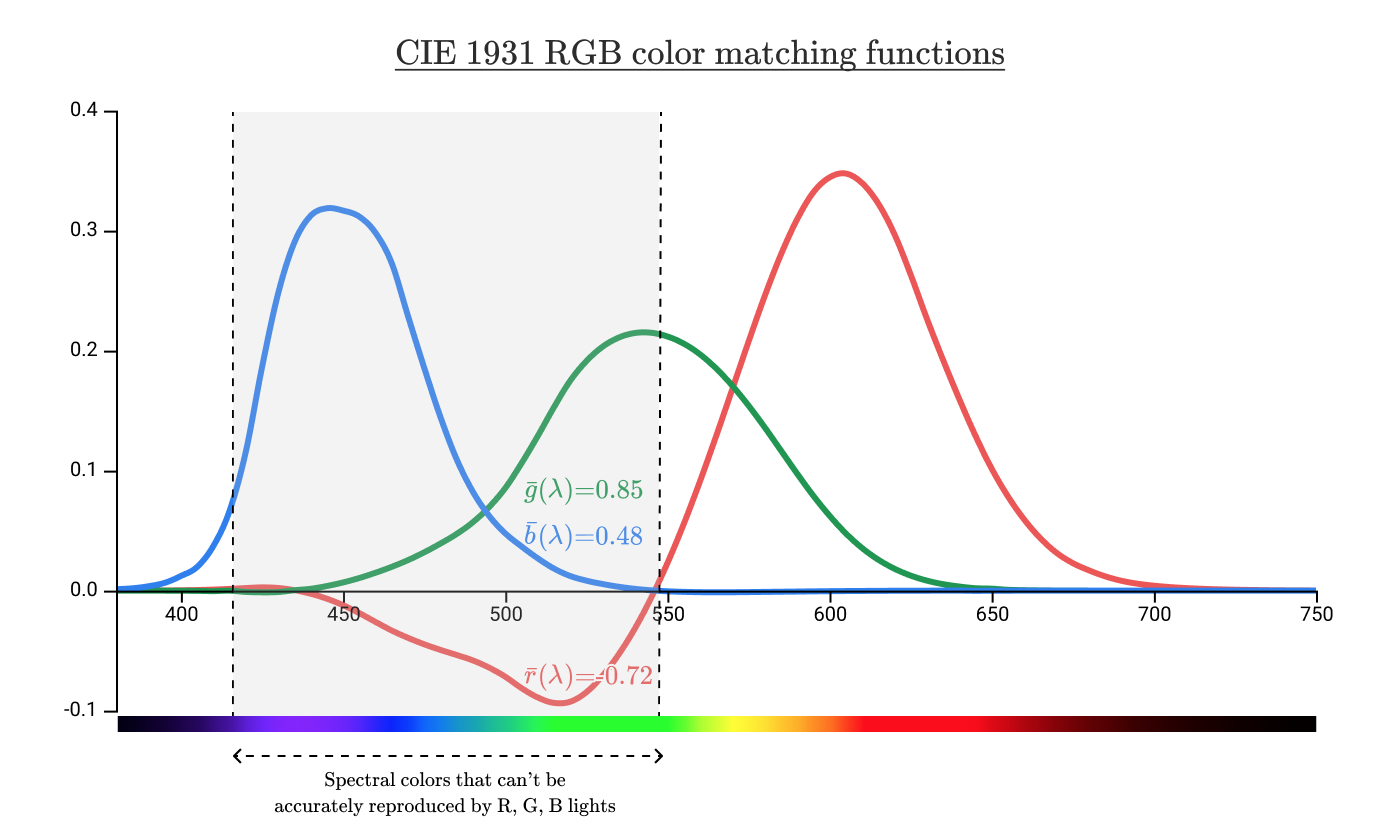
注釈: （破線矢印の下）RGBの光では正確に再現できないスペクトルの色

しかし、このグラフは、どのスペクトルの色が再現できないかを示すだけのものです。非スペクトル色はどうなのでしょうか？　R、G、Bの組み合わせでピンク色を作ることはできるでしょうか？　ティールの色（濃い青緑色）ならどうでしょう？

こうした質問に答えるには、色空間を視覚化するためのより良い方法が必要となります。

色空間と色度の可視化

これまでのほとんどのグラフでは、波長を横軸に、その他の値で対象とするものを縦軸に取り、複数の系列をプロットしたものでした。

注釈: （上の図の縦軸）等色関数
（下の図の縦軸）人間の錐体感度
（横軸）波長（nm）

今度は、色を（ R , G , B ）、あるいは（ L , M , S ）の関数でプロットしてみましょう。3D（ R , G , B ）空間にプロットされた色はどのように見えるでしょうか。

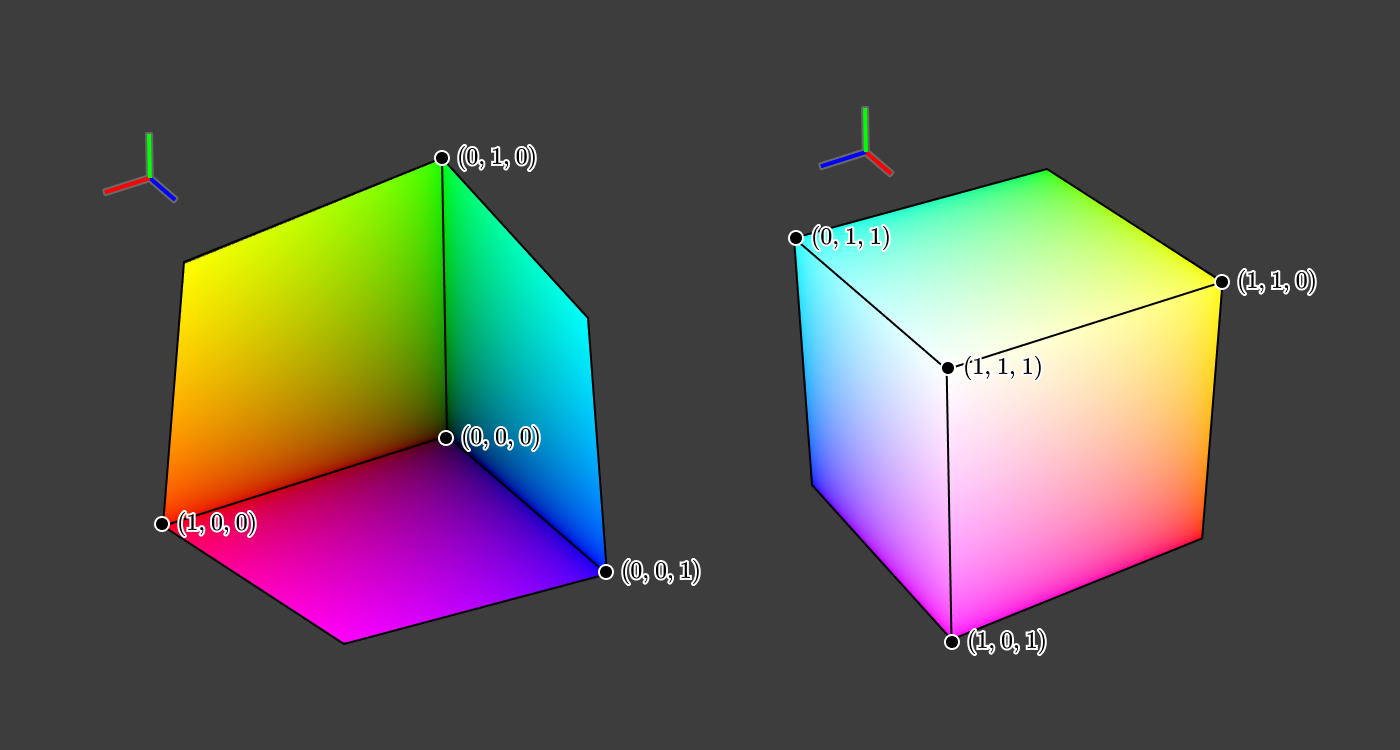
いいですね！　これにより、虹の色のスペクトルだけでなく、より幅広い色の組み合わせを視覚化できます。

これを2次元に落とす簡単な方法は、次のように値のペアそれぞれでプロットを作成することです。

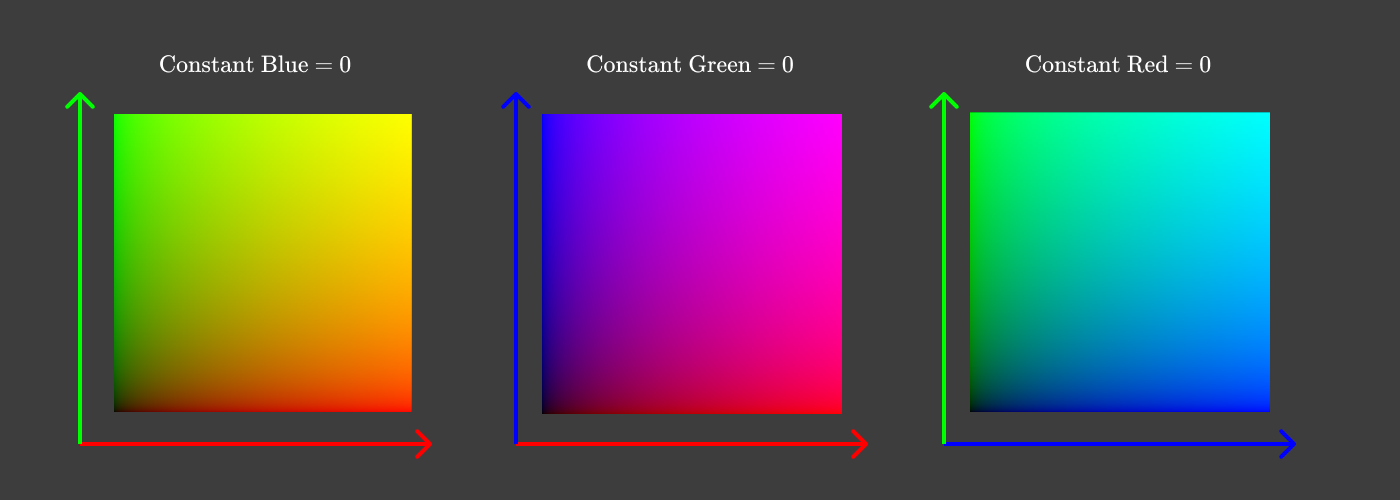
座標の1つの要素を固定し、残りの要素のペアでプロットした図

このようなプロットはいずれも、ある要素を一定に保つために、1つ次元を諦めなければなりません。赤、緑、青のうちの1つを一定に保つというのではなく、 明度 を一定に保ちつつ、虹の色、そしてその色の組み合わせ全てを示すプロットを作ることができたら最高です。

キューブの図をもう一度見てみましょう。（0, 0, 0）は黒、（1, 1, 1）は白であることが分かります。

では、このキューブを（1, 0, 0）、（0, 1, 0）、（0, 0, 1）で決まる平面で斜めに切ってみると、どうなるでしょうか？

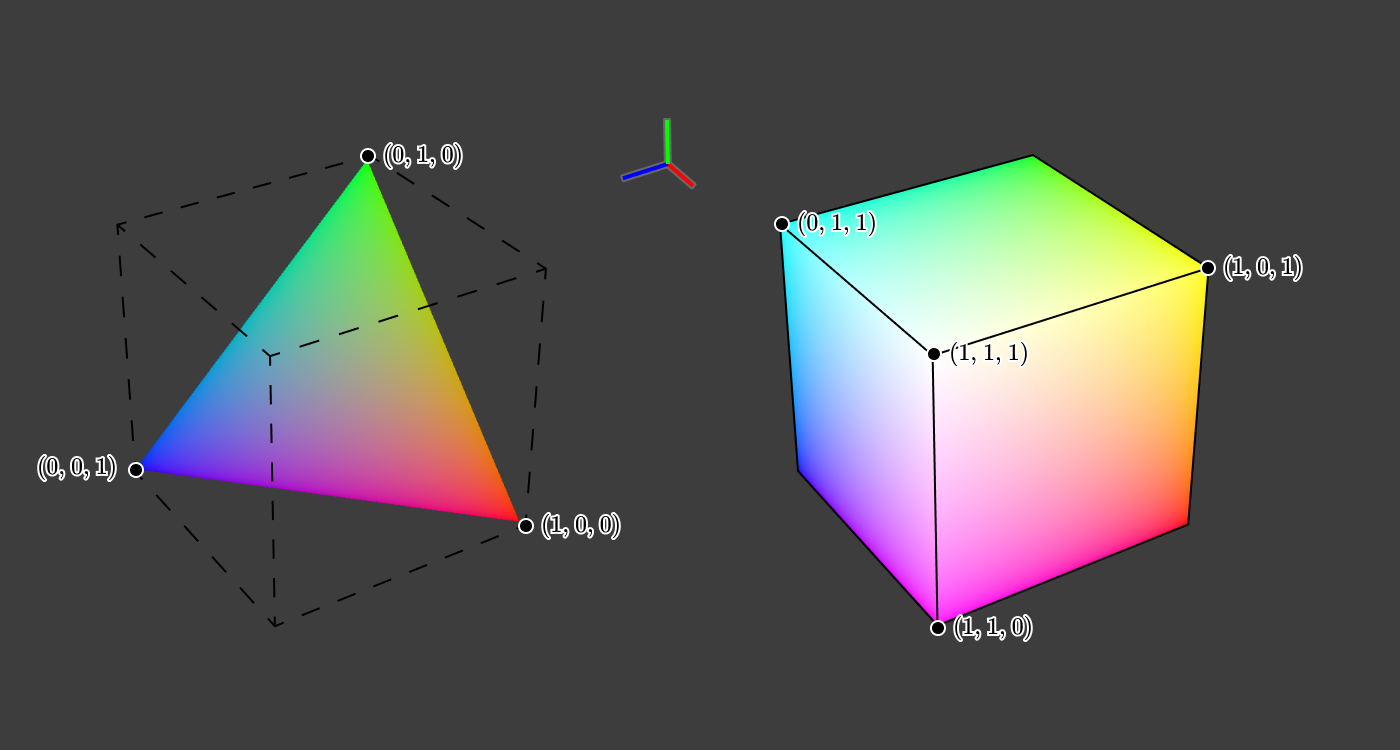
キューブにおけるこの三角形の断面は、 R + G + B =1の性質を有しています。つまり、明度のおおよその近似値として R + G + B を使うことができるのです。この三角形の断面を上から見ると、次のようになります。

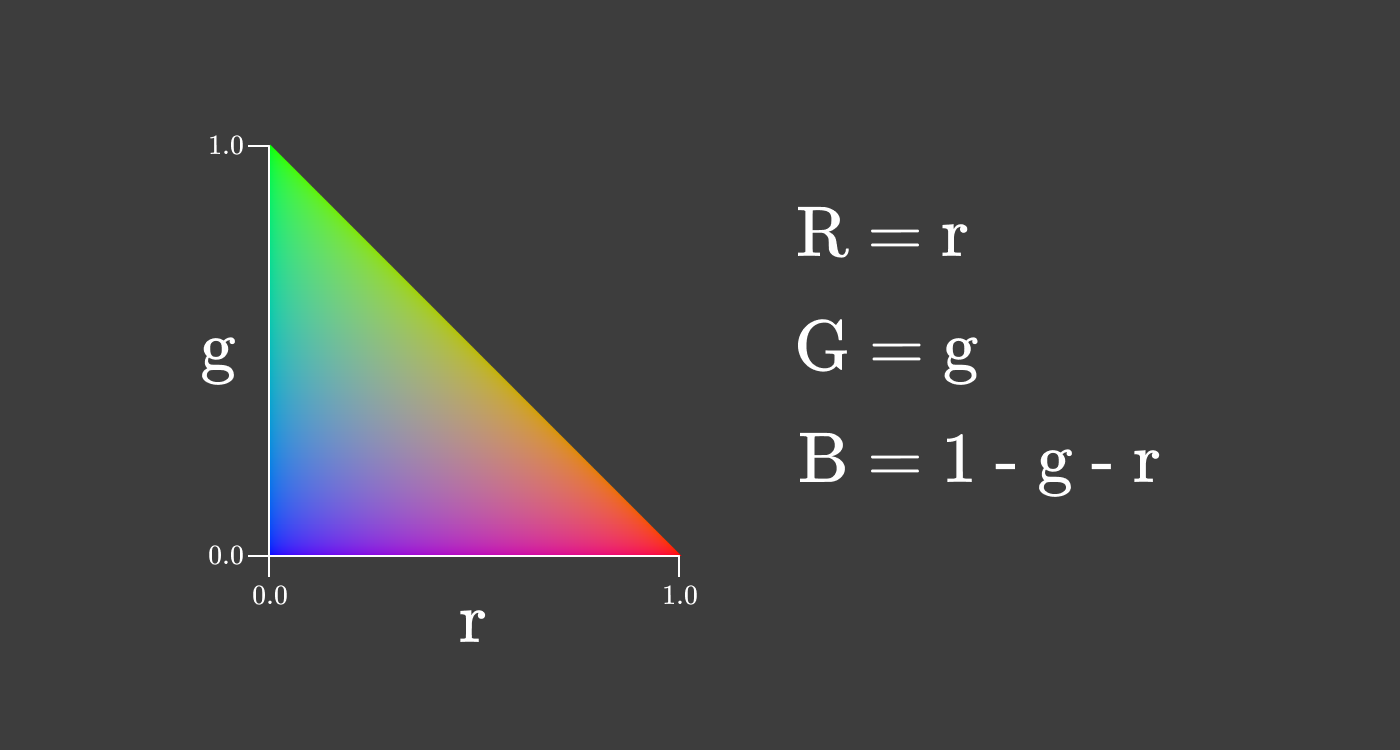
このように色を2次元で表現したものを 色度図 と言います。特に、この種類は rg色度図 と呼ばれます。色度図からは、明度を無視した原色の 比率 に関する情報が得られます。

つまり、様々な明度で同じ色度を得られるということです。

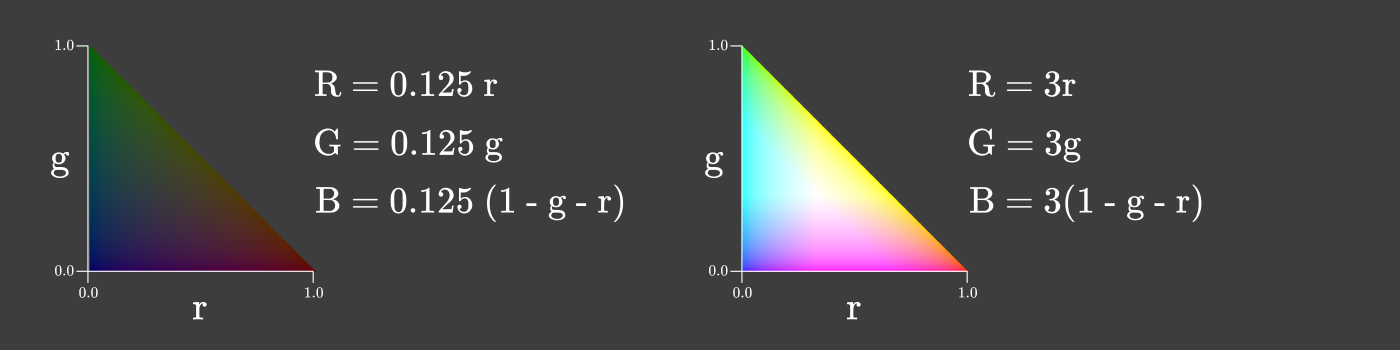
R , G , B の比率を維持しつつ明度が最大となるものを得るために、明度がrとgの変化によって変わる色度図を作ることもできます。

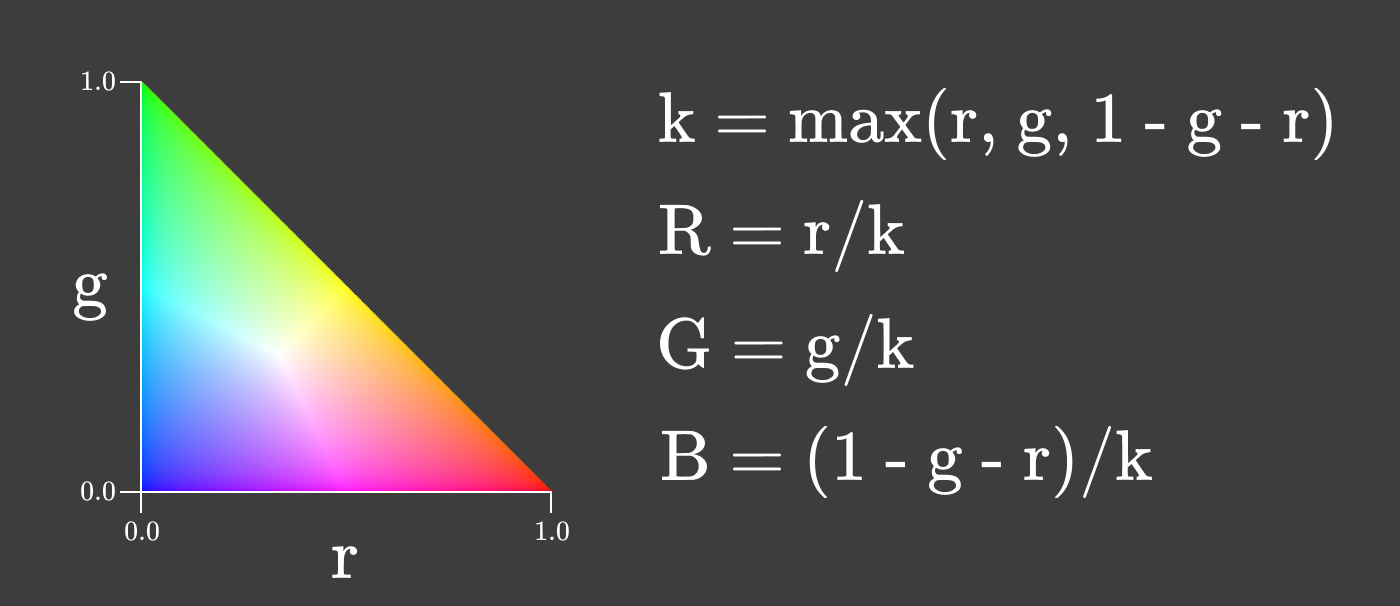
色度は、光源が同じスペクトル分布を持っているならば、明度が変化しても一定に保たれるので、色について考える際には便利な特性です。あなたが画面の明るさを変えてみても、色度は変わらないですよね！

他にも、色度を2次元に分ける方法はたくさんあります。一般的な方法の1つは、HSL色空間とHSV色空間の両方で使われます。次のように、どちらの色空間でも色度を「色相」と「彩度」に分けています。

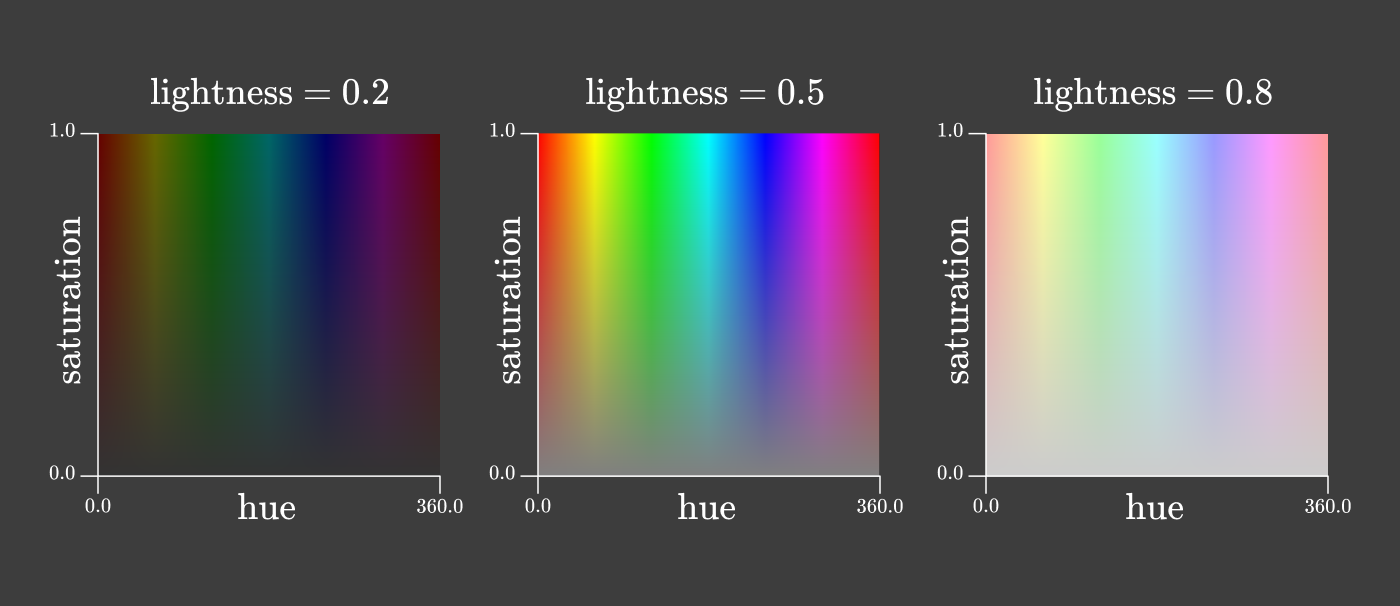
rg色度図の三角形と、上のような色相と彩度の四角形には、虹のあらゆる色が含まれていることがすぐに分かるのではないかと思います。それでは、等色関数における厄介な負の値について、もう一度見てみましょう。