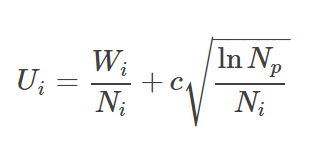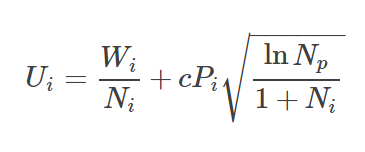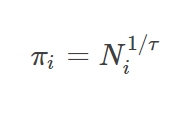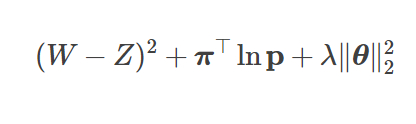2016年の3月、DeepMindのAlphaGoが人類最強の囲碁棋士を破った最初のAIとなり、衝撃が走りました。この時のAlphaGoのバージョンであるAlphaGo Leeは世界中の最高の囲碁棋士の膨大な対局を学習に使っていました。数日前に発表された 新しい論文 によると、新しいニューラルネットワークの AlphaGo Zero は人間が囲碁の打ち方を教える必要がないそうです。今までの囲碁棋士より(人間、機械に関係なく)優れているだけでなく、たった3日間の学習で打ち方を学んでしまうのです。この記事では、これがどのようにして可能なのか、そしてなぜ可能なのかについて説明します。

モンテカルロ木探索

離散的で決定論的な完全情報ゲームをするボットを作成できるアルゴリズムは、モンテカルロ木探索(MCTS)でしょう。囲碁やチェスやチェッカーのようなゲームをするボットは次の一手を決める際に全ての選択肢を試し、それに対し相手が取りうる手やその後の自分の手などをチェックします。囲碁のようなゲームでは、候補手がゲームが進むにつれ急速に増えていきます。

モンテカルロ木探索は、候補手を絞って良し悪しを判断し試す手を選びます。従って、打つ可能性の高い手に力を注ぐことになります。

注釈(左から右、上から下)
離散的で決定論的な完全情報ゲーム
両者とも全てが見える
対局者同士が競い合う
全ての手に複数の結果が伴う
それぞれが明確に独立した動きと位置

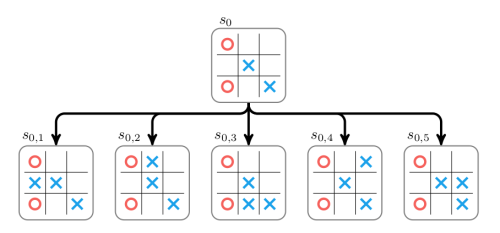
さらに技術的に言うと、アルゴリズムは次のように働きます。進行中のゲームが初期盤面s0にあり、ボットの順番になりました。ボットは A セットから手を選ぶことができます。s0のための単一ノードで構成された木を使ってモンテカルロ木探索が始まります。このノードは全ての a∈A 行動を試して 展開 され、それぞれの行動に対応する子ノードが構築されます。下記の図では三目並べを使ってこの展開を表しています。

それから新しい子ノードのそれぞれの値が見つけ出されます。子ノード内のゲームは、勝ち、負け、引き分けのいずれかに到達するまで、無作為に子の盤面からマスに打っていくことで 展開 されます。スコアは勝ちの場合+1、負けの場合−1、引き分けの場合は0になります。

上記の最初の子の無作為な展開の結果は+1と推定できます。この値は、必ずしも最善手を表すものではなく、展開の進行状況に応じて異なります。あるときは、展開を考えることなく実行して、均一に無作為に手を決めます。多くの場合は、典型的な無作為の戦略よりマシな戦略に従うことや、盤面の値を直接見積もることでより良い一手を打つことができます。それについては後で詳しく説明します。

上記で見たとおり、それぞれの子ノードの評価値で木を展開しました。ここで、2つのプロパティを持つことに注意してください。つまり、累積値 W とその配下での展開の実行回数値 N をプロパティとして保存します。ここでは、それぞれのノードを訪問したのは1回のみです。

その後、親の値と訪問回数が増えることで、子ノードからの情報は木の上方向へ伝播されていきます。親の累積値は、その子の合計累積値に設定されます。

モンテカルロ木探索は、ノードの選択と展開、そして上方向への新しい情報の伝播を複数のイテレーションで継続していきます。これで展開と伝播はできました。

モンテカルロ木探索は、負荷がかかることになるため、葉ノードを全て展開しません。その代わり、選択の段階で展開するノードを選び、利益の上がる(高い推定値を持つ)ノードと比較的未踏(訪問回数が少ない)ノードをうまく両立させます。

葉ノードは木を斜滑降して根ノードから選択されます。この時、UCT(Upper Confidence bound applied to Tree(探索木の信頼上限))の最高スコアを持つ子iを必ず選択します。

この時、 Wi は i 番目の子の累積値、 Ni は i 番目の子の訪問回数、 Np は親ノードの訪問回数です。パラメータ c ≥0は利益の上がるノード(低 c )と比較的未踏ノード(高 c )を選択する際にトレードオフを制御します。多くの場合、このパラメータは経験に基づいて設定されます。

c =1の三目並べの探索木のUCTスコア(U)は下記のとおりです。

この場合、最初のノードであるs0,1を選びます(引き分けの場合は、無作為に引き分けを解消するか、最初の有望なノードを選ぶことができます)。このノードは拡張され、値は上方向へ伝播されます。

各累積値 W はXの勝ち負けを反映します。選択時、Xの番かOの番かを把握し、Oの番時 W の符号を裏返します。

時間切れになるまで、モンテカルロ木探索は繰り返し実行されます。木は次第に展開され、(願わくば)可能な手を探索することで最善手を見極めます。ボットは実際に訪問回数が最も多い最初の子を選ぶことで、実際のゲームで予定していた手を打ちます。例えば、木の上部が次のような場合は下記のようになります。

すると、ボットは最初の手を選択し、s0,1へ進みます。

エキスパートポリシーで効率化

チェスや囲碁のようなゲームは分岐要素が非常に多くあります。ゲームのある盤面においては、候補手は多く、未来のゲームの盤面を十分に探索するのは非常に困難になります。その結果、チェスには推定で10 ⁴⁶ の ボード局面 があり、囲碁の場合では従来の19×19碁盤で打った場合、10 ¹⁷⁰ もの局面があります(三目並べはたったの5478局面です)。

一般的なモンテカルロ木探索を用いた次の手の検証の効率性は十分ではありません。打つ価値のある手に焦点を絞る必要があります。

ある盤面sにおいて、熟練レベルのプレイヤがそれぞれの候補手をどれだけの確率で打つのかを教えてくれる *エキスパートポリシー π* が存在したと想定します。その場合、三目並べの例を取ると下記のようになります。

上記で各 Pi =π（ai | s0） は、根ノードの盤面 So において、 i 番目の手である ai を選択する確率を示しています。

本当に優れたエキスパートポリシーであれば、 π が算出する確率に従って直接次の一手を引き出すか、いっそのこと、最も高確率の一手を取ることにより、強力なボットを生み出すことができます。残念ながら、エキスパートポリシーの入手は困難であり、あるポリシーが最適かどうかを検証することも同じく困難です。

ただし、ありがたいことに、モンテカルロ木探索を改変した形式を使ってポリシーの改善を図ることができます。更に、この改変バージョンは、ポリシーに従って各ノードの確率を格納します。この格納された確率は、選択の際にノードのスコアを調整するために用いられます。DeepMindが使用した、探索木の確率的な信頼上限スコアは次の通りです。

以前と同じく、スコアは、着実に高いスコアを生み出すノードと探索されないノードとの間のトレードオフとなります。ここでは、ノードの探索はエキスパートポリシーに沿った形になりますが、その際、エキスパートポリシーが、高確率だと考える一手への探索というバイアスがかかった状態になります。本当に優れたエキスパートポリシーであれば、モンテカルロ木探索は、ゲームの状況を有利な方向へ効率的に進めることに焦点を絞ります。もしエキスパートポリシーが劣っていれば、モンテカルロ木探索は、ゲームを不利な状況へ導くかもしれません。どちらの場合でも、サンプルが大きくなるにつれて、その制限内で、ノードの値は以前と同じように、勝利と敗北の比率である W i/ Ni に偏ります。

近似評価値を用いた効率化

効率的な形式の2つ目は、高コストで不正確な恐れのある無作為な展開を回避することで成し遂げられる可能性があります。1つ目の選択肢は、無作為な展開を導くために、前のセクションで言及したエキスパートポリシーを利用する方法です。そのポリシーが優れていれば、展開は、より現実的な熟達したレベルのゲーム進行を反映した形となるはずなので、盤面の評価値に関する見積もりの信頼性が高くなります。

2つ目の選択肢は、展開を一切回避することです。そして、近似値を取得する関数 ŵ(x) を使って直接、盤面の評価値の近似値を求めます。この関数は、盤面を入力すると展開を行わずに、直接[−1,1]内の値を計算します。もし ŵ が真の評価値に近い優れた近似値でありながら、展開よりも早く実行できる場合は、パフォーマンスを犠牲にすることなく実行時間が節約できることは明らかです。

モンテカルロ木探索の速度を上げるために、近似評価値の取得は、エキスパートポリシーと並列で使用することが可能です。ここで重要な問題点があります。どうやってエキスパートポリシーと評価関数を取得するかということです。そのようなエキスパートポリシーや評価関数を訓練するアルゴリズムは存在するのでしょうか。

Alpha Zeroニューラルネット

Alpha Zeroのアルゴリズムは、高速化したモンテカルロ木探索を用いた自己対戦によって、徐々に、より優れたエキスパートポリシーと評価関数を生み出します。エキスパートポリシーπと近似評価関数ŵは、どちらもディープニューラルネットワークによって表されます。実際、効率を上げるために、Alpha Zeroは1つのニューラルネットワークfを使っています。これは、ゲームの盤面を入力すると、次の一手の確率と盤面の評価値の近似値を出力します（実際は、それに先立つ8つの盤面を入力すると、インジケータがどちらの順番かを示します）。

f ( s )→[p, W ]

探索木の葉ノードは、ニューラルネットワークを使ってそれらを評価することで展開していきます。各子ノードは N =0、 W =0、ネットワークによる予測に対応した P で初期化されます。展開されたノードの値は予測値に設定され、この値は探索木へ伝搬されます。

選択と伝搬は変わりません。簡単に言えば、伝搬の間に親ノードの訪問回数は加算され、 W の値に従って、その評価値は増加します。

更に別の選択、展開、伝搬のステップを取ると、探索木は次のようになります。

Alpha Zeroのアルゴリズムの核となる考え方は、ニューラルネットワークの予測は改善可能だということです。そして、モンテカルロ木探索によって生成された対局は、訓練データを提供するために利用できます。ニューラルネットワークのポリシーの部分は、当初予測した s 0の確率 P から、 s 0について実行したモンテカルロ木探索によって取得されたより高い確率 π へと、訓練を通じて改善されます。モンテカルロ木探索の実行後に改善されたポリシーの予測は次のようになります。

ここでτは定数です。

ゼロに近いτの値は、モンテカルロ木探索の評価に従い、最善の一手を選択するポリシーを生み出します。

ニューラルネットの値評価の部分は、ゲームの最終的な勝ち、負け、引き分けの結果に合致するように予測値Zを訓練することによって改善します。その損失関数は次のようになります。

ここで、(W−Z)2は損失値、 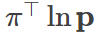はポリシーの損失です。
は、パラメータλ≥0及びニューラルネットワークにおけるパラメータ群を表すθを使った追加の正規化項です。

訓練は完全な自己対戦によって行われます。無作為に初期化されたニューラルネットワークのパラメータ θ のセットを使って訓練は開始されます。次に、このニューラルネットワークは、複数の自己対戦において使用されます。それぞれのゲームの各一手に対して、πを計算するためにモンテカルロ木探索が使われます。各ゲームの最終結果によって、ゲームの値であるZが決まります。パラメータ θ は、対局した盤面の状態を無作為に選択するために、損失関数の勾配降下を使って改善されます（または、より洗練・高速化されたいずれかの降下法を使います。Alpha Zeroは、Momentumを用いた確率的勾配降下法と共に、焼きなまし法を適用した学習率を使用しました）。

まとめのコメント

説明は以上となります。DeepMindの研究者たちは、自己対戦によって得たデータだけを効率的に使って、ゲームをプレイするエージェントを訓練するための簡潔で安定した学習アルゴリズムを生み出すことに貢献しました。現在のZeroのアルゴリズムは個別のゲームにのみ有効ですが、将来的に、MDP（マルコフ決定過程）や部分観測マルコフ決定過程に拡張されるようになるのか、今後が気になるところです。

AIの分野が非常に速い進歩を遂げている様子を目の当たりにするのは、実に興味深いことです。やがて人々を支配するようなロボットが現れるという主張には、耳を傾けるべきものがあります。AIが人間と同じレベルになるのはほんの一瞬で、あっという間に人間を追い越して超人レベルに到達してしまうでしょう。そうなったら、二度と後戻りすることはないのです。