目次

• 定義と構造
• 復元
• 確率分布
• コードサンプル：Deeplearning4jを使ったIrisで制限付きボルツマンマシンを起動する
• パラメータ及びkについて
• 連続的なRBM
• 結論及び次のステップ

定義と構造

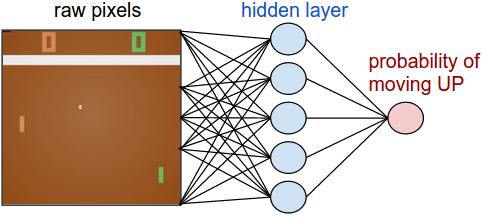
Geoff Hintonによって開発された制限付きボルツマンマシン（RBM）は、次元削減、分類、 回帰 、協調フィルタリング、特徴学習、トピックモデルなどに役立ちます。（RBMなどの ニューラルネットワーク がどのように使われるか、さらに具体的な例を知りたい方は ユースケース のページをご覧ください。）

制限付きボルツマンマシンは比較的シンプルなので、ニューラルネットワークを学ぶならまずここから取り組むのがよいでしょう。以下の段落では、図と簡単な文章で、制限付きボルツマンマシンがどのように機能するのかを解説していきます。

RBMとは浅い2層のニューラルネットであり、ディープビリーフネットワークの構成要素です。RBMの最初の層は可視層または入力層と呼ばれ、2つ目の層は隠れ層と呼ばれます。

上記の図の各円はニューロンのようなユニットを表しており、ノードと呼ばれます。ノードとは、単に演算が行われる場所のことです。このノードは違う層のノードとのみ接続し、同じ層内のノード間では接続を持ちません。

つまり層内での情報伝達はないのです。これが、制限付きボルツマンマシンの制限です。各ノードは入力を処理する演算の遺伝子であり、その入力を伝えるか否かの 確率的 決定を行うことから始めます。（確率的とは”ランダムに決定した”という意味で、この場合、入力値を調整する係数がランダムに決定されていることを指します。）

各可視ノードは学習すべきデータセットの中のアイテムから低次元特徴を抽出します。例えば、グレースケールの画像のデータセットから、各可視ノードは1つの画像における各画素の画素値を受け取ります。（MNISTの画像は784画素なので、それを処理するニューラルネットには可視層に784の入力ノードがあるということです。）

では、まずはひとつの画素値xを、2つの層にわたって見ていきましょう。隠れ層のノード1では、xに重みを乗算し、それをいわゆるバイアスに加算します。この2つの演算結果が、活性化関数に組み込まれます。活性化関数は、入力値xを与えられると、ノードの出力値、つまり活性化関数を通過する信号の強さを生成します。

activation f((weight w * input x) + bias b ) = output a

次に、複数の入力が隠れノードでどのようにまとめられるのか見てみましょう。各xに個別の重みが乗算され、その積がバイアスに加算され、その結果は活性化関数を通過しノードの出力値を生成します。

全ての可視ノードからの入力は全ての隠れノードに渡されますから、RBMは対称二部グラフとして定義できます。

対称とは、各可視ノードが各隠れノードに接続されていることを意味します（下記参照）。二部とは、2つの部分に分かれている、つまり2つの層を持つということで、グラフとはノードとノードの結合関係を表す数学的な用語です。

各隠れノードでは、各入力値xがそれぞれの重みwと乗算されます。つまり下記の例では、1つの入力値xが3つの重みを持ち、全部で12の重みを持つことになります（4つの入力ノード×3つの隠れノード）。2層間の重みで行列を作ると、行数は入力ノード数と常に等しく、列数は常に出力ノード数と等しいです。

各隠れノードは、それぞれ重みを乗算された4つの入力値を受け取ります。これらの積の合計を、さらにバイアス（少なくとも何かしらの活性化が起こるようになっている）に加算し、その演算結果が活性化アルゴリズムを通過し、各隠れノードに出力値を生成します。

この2つの層がより深いニューラルネットワークの一部だった場合、隠れ層No. 1の出力値は隠れ層No. 2の入力値として渡され、そこから先は最後の分類層に達するまで任意の数の隠れ層で同じ処理ができます。（シンプルなフィードフォワードの動きにするため、RBMのノードはオートエンコーダとしてのみ機能します。）

復元

ただし今回の制限付きボルツマンマシンのイントロダクションでは、深いネットワークのことはやりません。このネットワークが教師なし学習法（教師なしとは、テストセットに正解となるデータのラベルを用いないことです）でどのようにデータ復元のための学習がなされるのかに焦点を当て、可視層と隠れ層No. 1間の前方伝播と後方伝播をいくつか作っていきたいと思います。

復元のフェーズでは、隠れ層No. 1の活性化は後方伝播では入力になります。前方伝播においてxの重みが調整されるのと同時に、後方伝播ではノード間のエッジ1つずつに対し同じ重みが乗算されます。各可視ノードで、これらの積の合計は可視層のバイアスに加算され、これらの演算結果が復元データとなります。つまり、元々の入力の近似値となります。これを下記の図で表すことができます。

• 復元が新しい出力値となります
• このバイアスは新しい値です
• 活性化が新しい入力値となります
• 重みは均等です

RBMの重みは乱数で初期化されているため、復元と元々の入力値の差異が大きくなることが多いです。復元の誤差は r の値と入力値の違いだと考えることができます。反復学習のプロセスの中で、この誤差は最小になるまでRBMの重みに対して繰り返し逆伝播します。

逆伝播についてさらに詳細な説明を見たい方は こちら 。

このように前方伝播では、RBMは、ノードの活性化つまり 重み付けされた値xを与えられた時の出力値の確率 の推測を行うのに、入力値を用います。つまり p(a|x; w) です。

しかし、後方伝播では、活性化が導入され、復元つまり元データの予測結果が吐き出されると、RBMは与えられた活性化 a から入力値 x の確率を算出しようとします。これらは前方伝播で用いられたのと同じ係数で重み付けされています。この2つ目のフェーズは、 p(x|a; w) のように表現できます。

互いに、これら2つの推定値は入力xと活性化aつまり p(x, a) の同時確率分布を導き出します。

復元は、多くの入力に基づいて連続値を算出する回帰や、与えられた入力例に当てはまる個々のラベルを推測する分類とは異なった動きをします。

復元は元々の入力値の確率分布、つまり多くの異なる点の値を同時に推測するものです。これは 生成型学習 として知られるもので、分類で実行されるいわゆる識別学習とは区別しなければなりません。識別学習は、入力をラベルにマッピングし、データ点の集合の間に効果的に線を描く手法です。

ここでは、入力データと復元はどちらも形の異なる正規曲線であり、部分的に重なるものと考えてみましょう。

推定の確率分布と本当の入力値の分布の距離を測るために、RBMでは Kullback Leiblerダイバージェンス を使用します。数学的な詳しい説明は Wikipedia を参照してください。

Kullback Leiblerダイバージェンスは、2つの曲線について、重ならずに相違（ダイバージェンス）している領域を測ります。RBMの最適化アルゴリズムは、共有の重みに隠れ層の活性化を乗じた場合に、本来の入力の近似値を算出できるよう、この2つの領域の差を最小化しようとします。グラフの左側が、実際の入力値による確率分布pで、その右が復元された分布qです。下のグラフはその差の積分です。

2つの確率分布の差に基づいて重みを繰り返し調整することによって、RBMは、本来のデータに近似することを学習します。重みは次第に、最初の隠れ層の活性化でエンコードされた入力データの構造を反映するようになります。その学習過程は、2つの確率分布が徐々に1つのグラフに収束していく過程のように見えます。

確率分布

ここで少し、確率分布についてお話ししましょう。2つのサイコロを振って出た目の合計について確率分布を作成すると、次のようになります。

最も出る確率の高い結果は7で、サイコロを振った結果を予測しようとする数式は全て、そのことを考慮に入れる必要があります。

様々な言語は、文字の確率分布によって特定できます。どんな言語でも、ある特定の文字の使用頻度が他の文字よりも高いからです。英語では、eとtとaが最もよく使われます。一方、アイスランド語では、aとrとnが最もよく使われます。英語に基づく重み付けを使ってアイスランド語を復元しようとすると、相違が大きくなるでしょう。

同じように、どんな画像を含んでいるかによって、画素値が独自の確率分布を持つようなデータセットを思い浮かべてください。データセットがMNISTの手書きの数字を含むかどうかによって、画素値の分布は異なります。

もしくは、Labeled Faces in the Wildで入手できる顔の画像によっても、画素値の分布は異なります。

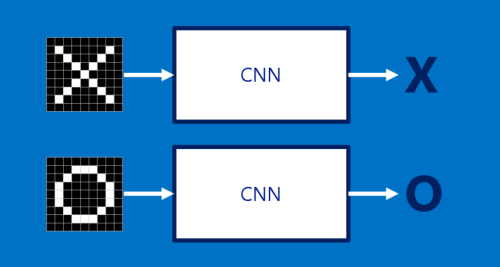
RBMが象と犬の画像だけを与えられたと想像してみましょう。出力ノードは象と犬、それぞれに対して1つずつです。RBMが前方伝播の際に考えるのは、「与えられたこれらの画素について、象と犬のどちらのノードにより重み付けをするべきか」ということです。後方伝播では、「象を与えられた時、どちらの画素の分布を予想するべきか」と考えます。

これが同時確率です。つまりaの場合のxと、xの場合のaが同時に起きる確率です。これはRBMの2つの層の共有の重みとして表されます。

復元を学習する過程とは、ある意味、与えられた一連の画像に対して、どちらの画素のグループが同時に起こりやすいかを学ぶことだと言えます。ネットワークの深部にある隠れ層のノードによって生成された活性化は、共起性が非常に高くなっています。例えば、”曲線的な灰色の管＋大きくてだらりと垂れた耳＋しわの多さ”などです。

上記の2つのイメージについて、RBMを実装した Deeplearning4j によって学習される復元を見てみます。これらの復元が表しているのは、本来のデータがどのように見えるとRBMの活性化が”考える”のかということです。Geoff Hintonは、これを、マシンが”夢を見ている”ようなものだと言っています。ニューラルネットのトレーニング中にレンダリングされた際、RBMが本当に学習しているということを確認するには、そうした視覚化は非常に有効なヒューリスティックです。もし学習していない場合は、この後検討しますが、ハイパーパラメータの調整を行うべきです。

最後にもう一点、RBMには、2つのバイアスがあることに気が付くと思います。これが、オートエンコーダとの相違点です。隠れたバイアスは、RBMが前方伝播を行う際に活性化を生成するのを助けます（データがどんなにわずかでも、少なくともいくつかのノードが活性化できるように底値を押し付けるからです）。 可視 層のバイアスはRBMが後方伝播する際に復元を学習する助けになります。

多層構造

このRBMがひとたび入力データの構造を学習して、最初の隠れ層の活性化に関連付けると、データはネットの下層に渡されます。すると今度は、最初の隠れ層が可視層の役割を担います。ここで出力結果は事実上の入力値となり、2層目の隠れ層のノードで重みを乗算します。そうして更に別の活性化が算出されます。

グループ化された特徴によってこの連続的な活性化のセットを生成し、それに続いて特徴のグループをグループ化する過程は、特徴の階層の基本です。それによって、ニューラルネットワークがより複雑で抽象的なデータの表現を学習するのです。

新たな隠れ層はそれぞれ、前の層からの入力に近づくまで重みが調整されます。これは、貪欲で層的な、教師なしの事前トレーニングです。ネットワークの重みを改善する際にラベルは不要です。つまり、ラベルなしのデータを使ってトレーニングできるということです。ラベルなしのデータは加工されていないデータで、世の中に存在する大部分のデータがそれに当たります。一般に、多くのデータにさらされたアルゴリズムほど、正確な結果を出します。そしてこれが、ディープラーニングのアルゴリズムが優れている理由の1つなのです。

これらの重みは既にデータの特徴に近似しており、より良い学習ができるように位置付けられているので、次のステップとして、この後に続く教師あり学習では、ディープビリーフネットワークで画像の分類に挑戦しましょう。

RBMには多くの利用方法がありますが、後の学習と分類を容易にしてくれる、重みの適切な初期化は、最大の長所です。ある意味、逆伝播に類似することを達成できます。つまり、モデルデータに十分な重みをかけるのです。事前トレーニングと逆伝播は互いに、同じ結果を得るための代替手段と言えます。

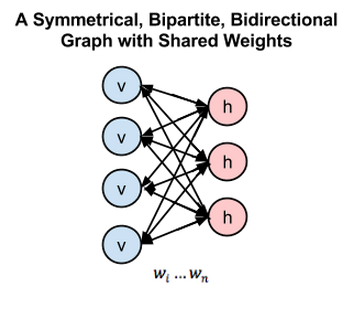
下の図は、RBMを1つのダイアグラムの中に合成した、双方向性を持つ対称二部グラフです。

注釈
重みを共有する、双方向性を持つ対称二部グラフ

より深い層のRBMの構造に関する学習に興味のある方への参考までに言うと、これらは 有向非巡回グラフ（DAG） の1タイプです。

コードサンプル：Deeplearning4jを使ったIrisで制限付きボルツマンマシンを起動する

より一般的なクラスにパラメータが与えられた NeuralNetConfiguration の層として、RBMを簡単に作成できることに留意してください。同様に、RBMのオブジェクトは、可視層に適用されるガウス変換や、隠れ層に適用される修正線形変換のように、プロパティをストアするために利用されます。

  final int numRows = 4;
    final int numColumns = 1;
    int outputNum = 3;
    int numSamples = 150;
    int batchSize = 150;
    int iterations = 100;
    int seed = 123;
    int listenerFreq = iterations/5;

    log.info("Load data....");
    DataSetIterator iter = new IrisDataSetIterator(batchSize, numSamples);
    // Loads data into generator and format consumable for NN
    DataSet iris = iter.next(); 

    iris.normalizeZeroMeanZeroUnitVariance();

    log.info("Build model....");
    NeuralNetConfiguration conf = new NeuralNetConfiguration.Builder()
        // Gaussian for visible; Rectified for hidden
        // Set contrastive divergence to 1
        .layer(new RBM.Builder(HiddenUnit.RECTIFIED, VisibleUnit.GAUSSIAN, 1)
            .nIn(numRows * numColumns) // Input nodes
            .nOut(outputNum) // Output nodes
            .activation("tanh") // Activation function type
            .build())
        .seed(seed) // Locks in weight initialization for tuning
        .weightInit(WeightInit.DISTRIBUTION) // Weight initialization
        .dist(new UniformDistribution(0, 1)) 
        // ^^ Weight distribution curve mean and st. deviation
        .lossFunction(LossFunctions.LossFunction.SQUARED_LOSS) 
        .learningRate(1e-1f) // Backprop step size
        .momentum(0.9) // Speed of modifying learning rate
        .regularization(true) // Prevents overfitting
        .l2(2e-4) // Regularization type L2
        .optimizationAlgo(OptimizationAlgorithm.LBFGS) 
        // ^^ Calculates gradients
        .constrainGradientToUnitNorm(true)
        .build();
    Layer model = LayerFactories.getFactory(conf.getLayer()).create(conf);
    model.setListeners(Arrays.asList((IterationListener) new ScoreIterationListener(listenerFreq)));

このコード は gist-it から引用しました。 こちら を参照してください。
src/main/java/org/deeplearning4j/rbm/RBMIrisExample.java

上記のコーディングは、 Iris flowerのデータセットを処理するRBM のサンプルです。これについては、別にチュートリアルがあります。

パラメータ及びkについて

変数kは コントラスティブダイバージェンス を実行する回数です。コントラスティブダイバージェンスは、学習が起きない間に、勾配を計算する際に用いられる方法です（勾配はネットワーク間の重みと差異の関係を表しています）。

コントラスティブダイバージェンスが実行されると、それは毎回、制限付きボルツマンマシンを構成するマルコフ連鎖のサンプルになります。典型的な値は1です。

上記の例では、より一般的な MultiLayerConfiguration を使って、RBMが層として形成される様子を見ることができます。各ドットの後ろを見れば、ディープニューラルネットの構造やパフォーマンスに影響を及ぼす追加パラメータが分かるのです。このサイト上では、そういったパラメータの大部分を定義しています。

weightInit （ weightInitialization ）は、各ノードに入ってくる入力信号を増幅またはミュートする係数の初期値を表しています。適切に重みを初期化すれば、訓練時間を大幅に短縮することができるのです。ネットワークの訓練は、ネットワークが正確な分類を行うために、最適な信号を送るよう係数を調整しているにすぎないからです。

activationFunction （活性化関数）とは、各ノードの閾値を決定する関数の1つです。閾値を上回る場合は信号がノードを通過し、閾値に満たない場合は信号が遮断されます。ノードが信号を通過させた場合は、「活性化している」ということです。

optimizationAlgo とは、ニューラルネットが段階的に係数を調整しながら、誤差を最小化したり、最小誤差の位置を特定したりする方法のことです。 複数の発案者たちのラストネームの頭文字を取って名づけられたLBFGSは、二階微分値を利用して、係数が調整される勾配を計算する最適化アルゴリズムです。

l2のようなregularization（正規化）の方法 は、ニューラルネットにおけるオーバーフィッティングに対抗するのに役立ちます。係数が大きいと、ネットが学習する結果に重み付けの大きな入力が残ることを意味するので、正規化は基本的に大きな係数にペナルティを与えます。重みが非常に強いと、新たなデータにさらされた場合に、ネットのモデルを一般化するのが難しくなる可能性があります。

VisibleUnit（可視ユニット）／HiddenUnit（隠れユニット） とは、ニューラルネットワークの層のことです。 VisibleUnit または可視層と呼ばれる層は、入力がなされるノードの層で、 HiddenUnit は、それらの入力がより複雑な形状で再結合される層です。どちらのユニットにも変換と呼ばれるものがあります。今回の場合、可視ユニットではガウス変換、隠れユニットでは修正線形がそれぞれの層から出る信号を新たな空間へ位置付けます。

lossFunction（損失関数） とは、誤差、つまりネットワークの予測とテストセットに含まれる正しいラベルとの差異を測定する方法です。ここで SQUARED_ERROR を使うと、すべての誤差が正になり、和の計算や逆伝播が可能になります。

momentum（モーメンタム） のような learningRate（学習率） は、ニューラルネットが誤差を修正する度に係数をどのくらい調整するかに影響を及ぼします。これらの2つのパラメータは、ネットが局所最適に向かう勾配を求めるステップのサイズを決定するのに役立ちます。学習率を大きくすると、学習速度が速くなり、最適値を越えてしまうかもしれません。学習率を小さくすると、学習速度が遅くなり、非効率になる可能性があります。

連続的なRBM

連続的な制限付きボルツマンマシンとは、種類の異なるコントラスティブダイバージェンスのサンプルを通じて、連続入力（小数点以下を切り捨てた数字）を受け入れるRBMの形式です。これにより、0と1の間の小数に正規化される画像画素やワードカウントベクトルのようなものを処理することができます。

注目すべき点は、ディープラーニングネットの全ての層が入力、係数、バイアス及び変換（活性化アルゴリズム）という4つの要素を必要としているということです。

入力とは、前の（あるいは元データとしての）層から加えられた数値データ、ベクトルのことです。係数とは、各ノード層を通過する様々な特徴に与えられる重みのことです。バイアスは、層内のノードが何であろうと確実に活性化されるようにします。変換とは、データが各層を通過した後、勾配を簡単に計算できるように（勾配はネットの学習に必要なものです）データを圧縮する追加アルゴリズムのことです。

追加アルゴリズムとその組み合わせは層によって異なる可能性があります。

効果的な連続的な制限付きボルツマンマシンは、可視層（または入力層）でガウス変換を採用し、隠れ層で修正線形ユニット変換を採用しています。この方法は 顔の復元 の際に、特に役立ちます。RBMでバイナリデータを処理するには、単に両方の変換をバイナリ変換にするのです。

ガウス変換はRBMの隠れ層にはあまり効果的ではありません。その代わりに使用される修正線形ユニット変換は、バイナリ変換よりも多くの特徴を表すことができます。バイナリ変換は ディープビリーフネット で採用しているものです。

結論及び次のステップ

RBMの出力数は割合として解釈することができます。復元の数字が0でない場合は常に、RBMが入力を学習したという良い兆候を示しています。制限付きボルツマンマシンを動かすメカニズムを別の視点から見るには、 ここ をクリックしてください。

次回は、 ディープビリーフネットワーク を実装する方法をお見せします。ディープビリーフネットワークは、多くの制限付きボルツマンマシンが相互に積み重なったものにすぎません。