2015年11月3日
ディープラーニングのサマースクールで学んだ26のこと
本記事は、原著者の許諾のもとに翻訳・掲載しております。
(訳注:2015/11/4、いただいた翻訳フィードバックを元に記事を修正いたしました。)
8月の初めに、モントリオールでディープラーニングのサマースクールに参加することができました。サマースクールは10日間にわたるもので、著名なニューラルネットワークの研究者の講演で構成されていました。この10日間で、私は1件のブログ投稿にはまとめきれないほど多くの事を学びました。ここで私は、60時間で得られたニューラルネットワークの知識をそのままお伝えしようと試みるのではなく、1パラグラフに要約できるようなちょっとした面白い情報のリストを作ることにしました。
これを書いている現在、 サマースクールのウェブサイト は現存しており、全てのプレゼンテーションのスライドが載せられています。全ての情報とイラストはこれらのスライドから利用しており、権利はそれぞれのオリジナルの著者に帰属するものです。またサマースクール内の講演は録画もされており、その動画も同様に閲覧可能になるでしょう。
追記 : ディープラーニングのサマースクールのビデオが公開されました 。
それでは始めましょう。
1. 分散表現の必要性
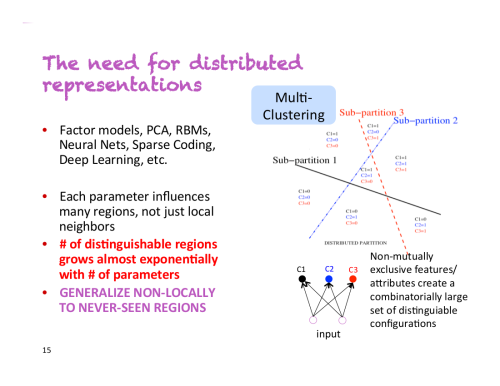
Yoshua Bengio氏は彼の最初の講演で「これが私の最も重要なスライドです」と述べました。そのスライドがこちらです。
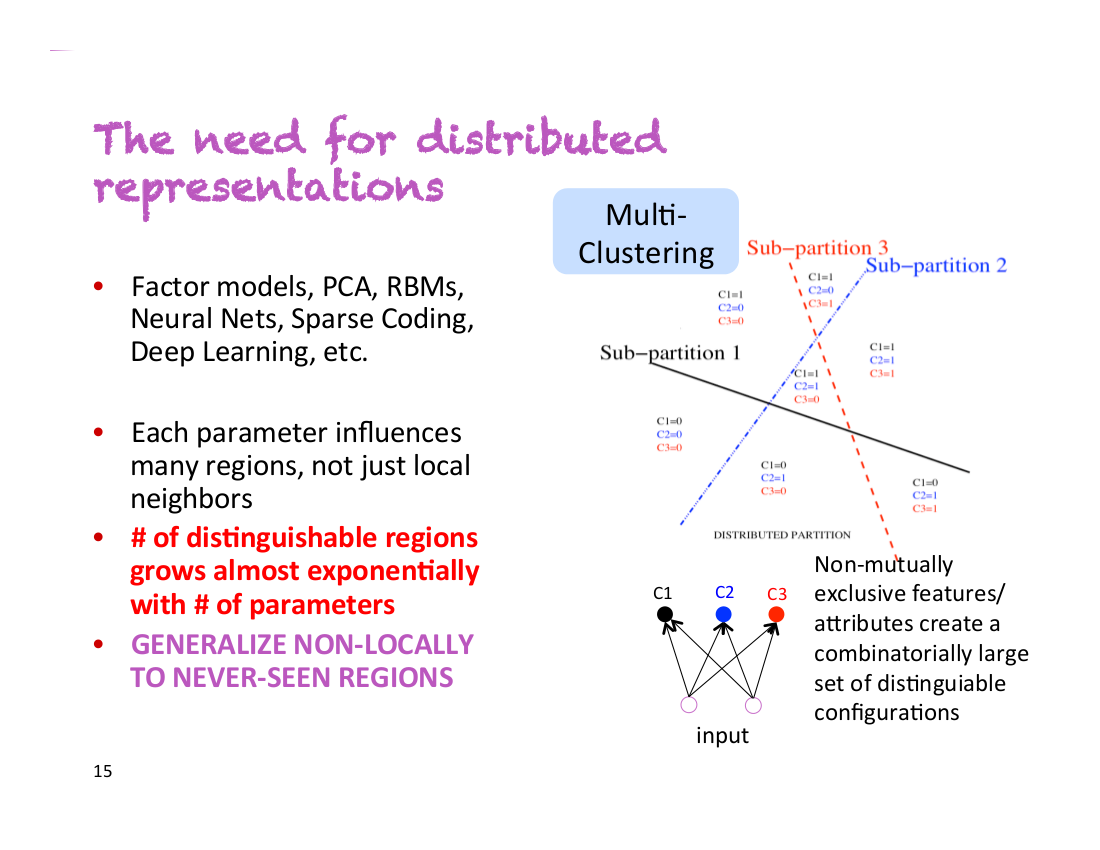
ある人が男性か女性か、眼鏡をしているかしていないか、長身かそうでないかを分類する分類器があると仮定しましょう。非分散表現では2*2*2=8個の異なる人のクラスを扱うことになります。正確な分類器になるよう学習するには、8クラスそれぞれについて十分な数の訓練データが必要になります。しかし、分散表現の場合、それぞれの性質を異なる次元でとらえることができるのです。これはつまり、「分類器が今までに『背が高く、眼鏡をした男性』のサンプルを見たことがなくても、他の全てのサンプルから性別・眼鏡の有無・背の高さをそれぞれ個別に学習したことによりこれを識別できる」ということです。
2. 高次元においては局所解は問題にならない
Yoshua Bengio氏のチームは、「高次元のニューラルネットのパラメータを最適化するとき、局所解は事実上存在しない」ということを実験的に突き止めました。代わりに、全次元のうち数次元のみにおいて極値を取る鞍点が存在します。つまり、パラメータのトレーニングはこういった鞍点において急に遅くなり、その点からどう脱出するかをニューラルネットワークが突き止めるまでその状態は続きます。突き止めるまで訓練を待つと訓練が長くなるので、それまで訓練させるように設計者が望んで待つ場合にしか脱出は起こりません。
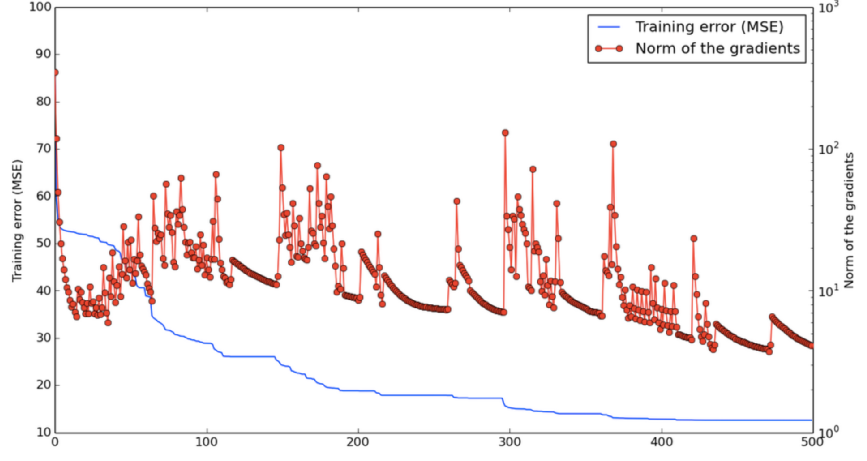
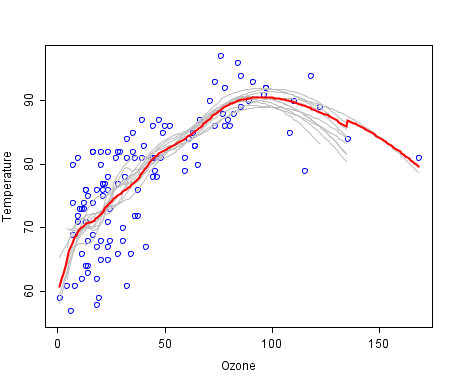
以下のグラフは、「鞍点への接近」「鞍点からの脱出」の2つの状態を行き来するニューラルネットワークのトレーニング過程を表すグラフになります。
ある特定の1つの次元について、「ある点が大域解ではない局所解である」確率が p
という小さな確率だとします。すると、1000次元空間上のある点が 全ての 次元において誤った局所解である確率は p¹⁰⁰⁰ となり、これは天文学的に低い確率になります。しかし、 ごく数次元 においての局所解を取る確率は極めて高いのです。そういった局所解に陥った場合に、脱出すべき正しい方向を見つけるまでの間そこに捕らわれているように見えてしまいます。
加えてこの確率 p は損失関数が大域解に近づけば近づくほど高くなります。たとえ本当に局所解である箇所で探索を止めてしまっても、どのみち大域的な最適解の近くであることにはなるため、問題はないということになるのです。
3. 導関数・導関数・導関数
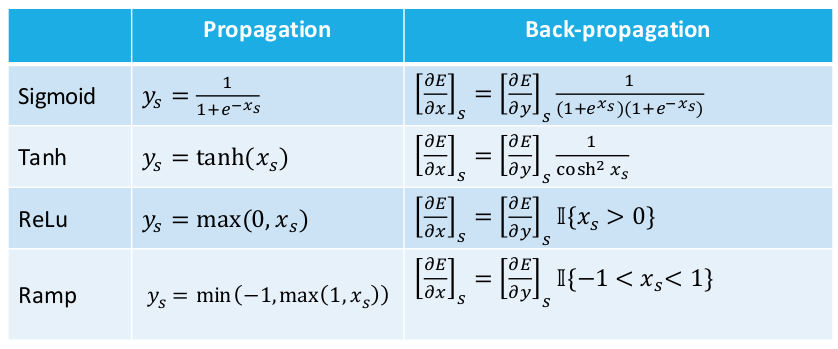
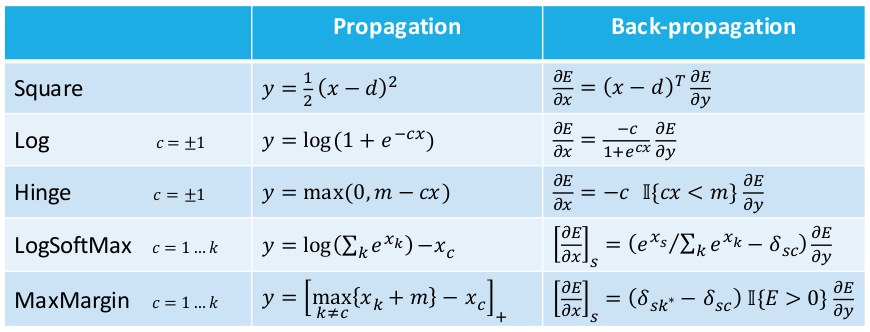
Leon Bottou氏は、活性化関数と損失関数、およびそれぞれに対する導関数に関する有用な表をプレゼンしてくれました。後々のためにここで示しておきます。
Update : コメントで指摘があったように、Ramp式における最小/最大関数は変更する必要があります。
4. 重みの初期化にまつわる戦略
ニューラルネットワークの重み付けの初期値を定める際について、現在推奨されている手法は、 [ − b, b] から一様にサンプリングされた値を W_(i, j)^((k)) とするものです。ここでは
$ b = \sqrt{\frac{6}{H_k + H_{k+1}}} $
とします。
H(k) と H(k + 1) は重み行列の前後の隠れ層の個数に相当します。
Hugo Larochelle氏の講演で紹介されたもので、論文としての初出はGlorot & Bengio (2010)からのものです.
5. ニューラルネットのトレーニングのコツ
Hugo Larochelle氏は、実践的な提案をいくつか紹介していました。
- 実数値を規格化すること。全ての値について平均値を引き、標準偏差で割る。
- 訓練中は学習レートを下げること。
- ミニバッチ学習で勾配を更新することできます。ミニバッチ学習では勾配がより安定的になります。
- 学習が停滞状態に陥ったのを脱出させるために、モーメントを使うことができる。
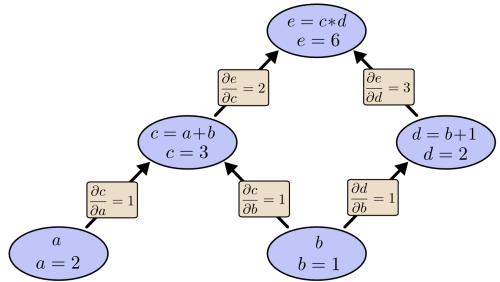
6. 勾配のチェック
自分で実装したバックプロパゲーションが上手く機能しない場合、99%の確率で勾配の計算にバグがあります。問題の特定のために、勾配のチェックをしましょう。
勾配の定義を使うための考え方は次のように言えます。「ある重み付けを少量増やした場合、モデルの誤差がどのぐらい変化するか」
$ \frac{\partial f(x)}{\partial x} \approx \frac{f(x+\epsilon) – f(x-\epsilon)}{2\epsilon} $
より詳細な説明はここから見ることができます。: Gradient checking and advanced optimization
7. 動きのトラッキング
人間の動きはは驚くほど正確にトラッキングできます.以下はGraham Taylor氏らによる2010年の論文、 Dynamical Binary Latent Variable Models for 3D Human Pose Tracking からの例です。この手法では条件的制限付きボルツマンマシンを利用しています。
8. シンタックスか、シンタックス無しか?(あるいは、「シンタックスは思考するか?」)
Chris Manning氏とRichard Socher氏は、伝統的な構文解析手法にニューラルな手法を組み合わせた合成モデルの開発について多大な努力をしてきました。構文木に沿って単語の意味を結合していく際に、加算的/乗算的な相互作用を用いる Recursive Neural Tensor Network (Socher et al., 2013)という論文はその最たるものと言えます。
その後、そのモデルに対して(大きく差をつけて)成果を挙げたのが Paragraph Vector (Le & Mikolov, 2014)という論文ですが、この論文は、文の構造やシンタックスについての知識を全く与えずに行うものでした。Chris Manning氏はこれについて、「『良い』合成ベクトルを作ることに負けた」と言及していました。
しかし、最近では構文木を使ったさらなる研究がこれを上回る結果を打ち出しました。 IrsoyとCardieの論文(NIPS, 2014) では前述のParagraph Vectorに打ち勝つために、複数次元においてネットワークをより”深化”させました。最終的に、 Tai氏らの論文(ACL, 2015) がLSTMと構文木の組合せによりさらにその結果を向上させています。
これらのモデルの、5分類の感情に関するスタンフォードのデータセットでの結果が以下の通りです。
| 手法 | 精度 |
|---|---|
| RNTN (Socher et al. 2013) | 45.7 |
| Paragraph Vector (Le & Mikolov 2014) | 48.7 |
| DRNN (Irsoy & Cardie 2014) | 49.8 |
| Tree LSTM (Tai et al. 2015) | 50.9 |
現段階では、構文木を使ったモデルがシンプルなアプローチよりも上回っているように見えます。シンタックスに依存しない新たな手法が現れてこの競争に勝つのか、それが起こるとしたらいつか、ということに私は興味津々です。何と言っても、多くのニューラルモデルのゴールは文法を捨て去ることではなく、同じネットワークで暗示的にそれを捉えることにあるのです。
9. Distributed と distributional
Chris Manning氏は、混用されがちな以下の2単語についてその意味を明確に示しました。
Distributed : 多くの要素の連続的な活性化レベルのこと。Dense word embeddingのように、ワン・ホットなベクトルと対比される。
Distributional : 使われるコンテクストによって表される。 Word2vecはdistributionalだが、カウントベースの単語ベクトルもdistributionalである。単語の意味をモデリングするのに言葉のコンテクストを用いるため。
10. 依存文法解析の現状
Penn Treebankにある、依存文法解析の比較を以下に示します。
| 解析器 | ラベルなしの精度 | ラベル付きの精度 | スピード (文/秒) |
|---|---|---|---|
| MaltParser | 89.8 | 87.2 | 469 |
| MSTParser | 91.4 | 88.1 | 10 |
| TurboParser | 92.3 | 89.6 | 8 |
| Stanford Neural Dependency Parser | 92.0 | 89.7 | 654 |
| 94.3 | 92.4 | ? |
一番下の結果は、スタンフォードのニューラル解析器のトレーニングにGoogleが多大な量のリソースを利用して行った結果のものです。
11. Theano
実のところ、以前は Theano について少ししか知らなかったのですが、サマースクールの間に色々と学ぶことができました。これはとても素晴らしいものです。
Theanoはモントリオールで生まれたライブラリなので、その開発者たちに直接質問できたのが特にためになりました。
ほとんどの情報は interactive python tutorials という形でネット上で入手可能です。
12. Nvidia Digits
Nvidiaは、 Digits というツールキットを有しています。これは、一切のコーディングを要せずに複雑なニューラルネットワークモデルを訓練したり可視化したりできるものです。また、NvidiaはDigitsや他のディープラーニングのソフト(TheanoやCaffeなど)を実行するためにカスタマイズした DevBox というマシンも販売しています。Titan XのGPUを4つ搭載しており、現在$15,000という価格になっています。
13. Fuel
Fuel は、データセット上での繰り返しをマネジメントしてくれるツールキットです。ミニバッチへの分割やシャッフル、様々な前処理の適用などができます。また、MNISTやCIFAR-10、Googleの10億語のコーパスなどの既存データセット用に作られた関数などもあります。これはTheanoでのネットワーク構築をシンプルにしてくれる Blocks というツールキットと併用するようにデザインされています。
14. マルチモーダルな言語の規則性
“王様 – 男 + 女 = 女王”というのをご存知でしょうか?画像上でこれができることが示されています(Kiros et al., 2015).
15. テイラー展開近似式
現在 x₀ にいるところから x へ移行しようとするとき、新しい点での関数の値は導関数によって概算することができます。テイラー展開を用いるのです。
$ f(x) = f(x_0) + (x – x_0)f'(x) + \frac{1}{2} (x – x_0)^2 f”(x) + … $
同様に、パラメータを θ₀ から θ に更新したときの関数の損失についても概算が可能です。
$ J(\theta) =J(\theta_0) + (\theta – \theta_0)^T g + \frac{1}{2} (\theta – \theta_0)^T H(\theta – \theta_0) + … $
ここで、 g には θ に対応する導関数が含まれており、また H は θ に対応する2次導関数のヘッセ行列です。
これはテイラー展開による2次近似ですが、さらに高次の導関数も用いることによりさらに精度を向上させることができます。
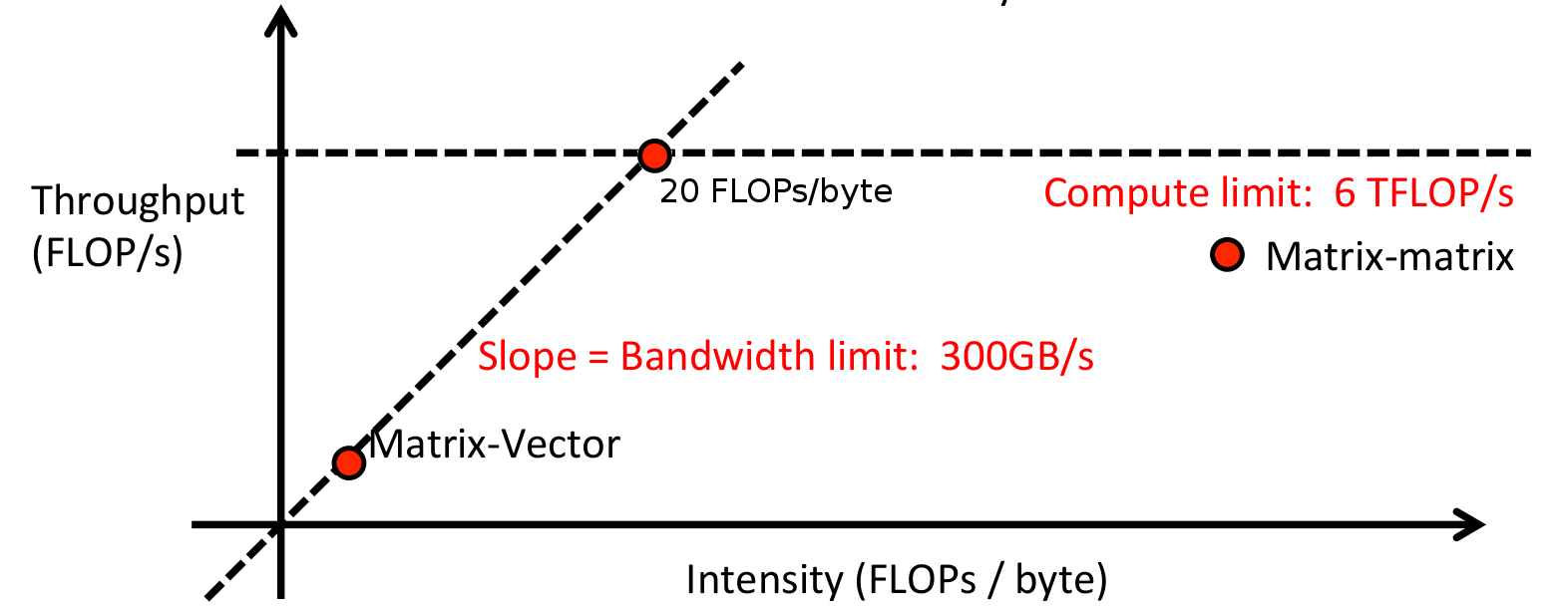
16. 演算密度
Adam Coates氏は、GPU上での行列計算の速度を解析するための手法について講演してくれました。これは、処理時間が「メモリ読み書き」「計算の実行」のどれに費やされているかを示す簡略化されたモデルです。どちらも並列的に行えると仮定し、どちらがより時間を取るかについて調べます。
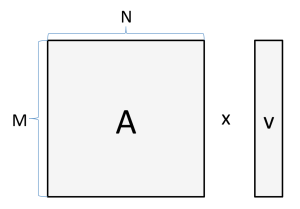
例として、ベクトルに行列を掛ける計算を考えます。
M = 1024 で N = 512 の場合、読み書きしなければならないバイト数は以下のようになります。
4 bytes × (1024 × 512 + 512 + 1024) = 2.1e6 bytes
そして、必要な計算回数は以下の通りです。
2 × 1024 × 512 = 1e6 FLOPs
6 TFLOP/sのGPUと、300GB/sの帯域幅のメモリで計算する場合、トータルの実行時間は以下の通りになります。
$ \text{max}\{2.1e6\text{ bytes }/ (300e9\text{ bytes}/s), 1e6\text{ FLOPs} / (6e12\text{ FLOP}/s) \} \\ = \text{max}\{ 7\mu s, 0.16\mu s \} $
つまり、このプロセスはメモリへの読み書きに費やされる 7μ**s という時間がネックとなり、GPUを速いものにすることには効果がないという事になります。おそらくこれは読んでいる方も推測しているとおり、より大きな行列やベクトルの計算をする場合、あるいは行列と行列を掛ける場合においては、この状況は改善されます。
また、Adam氏は、ある処理の密度を計算するためのアイデアを解説していました。
密度 = (算術処理の数) / (読み書きするバイト数)
先ほどのシナリオで言えば、
密度 = (1E6 FLOPs) / (2.1E6 bytes) = 0.5 FLOPs/bytes
となります。低い密度は「メモリがボトルネックである」ということを、高い密度は「GPUがボトルネックである」という事を示します。これは、システム全体をスピードアップするにはどちらを改善する必要があるのか、どこにスイートスポットがあるのかを発見するためにビジュアライズが可能です。
17. ミニバッチ
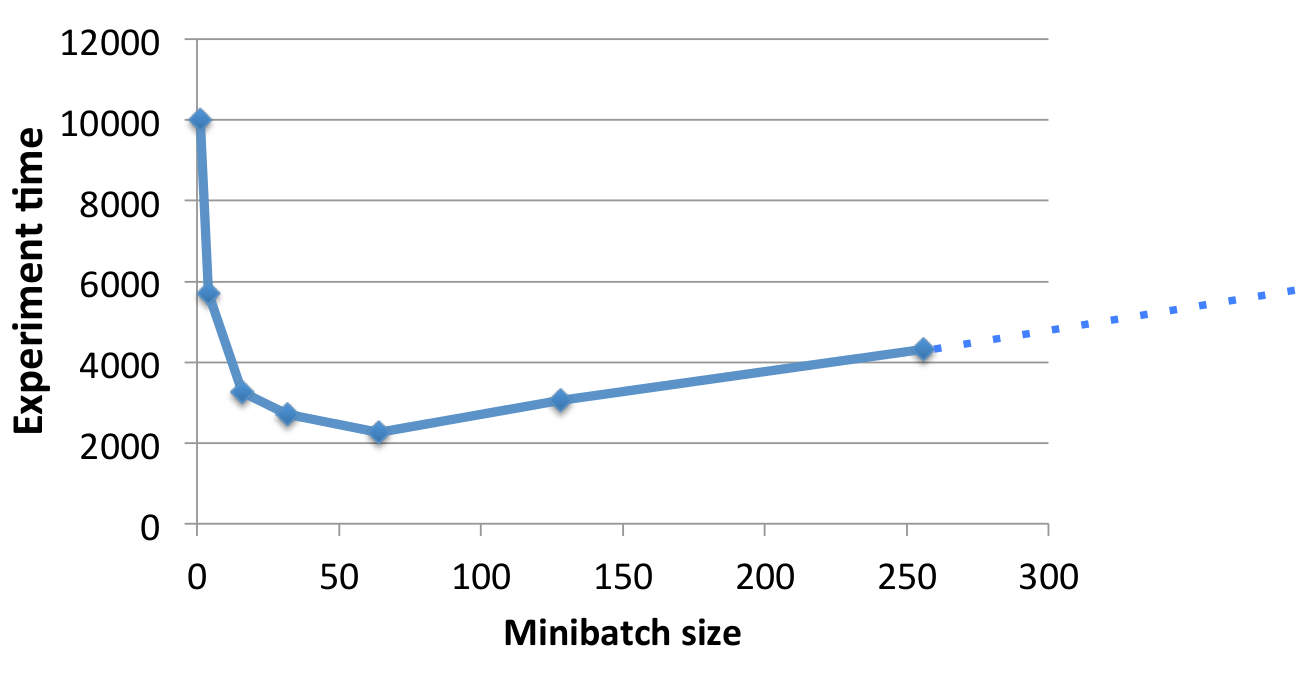
密度計算から続いて、ネットワークの計算密度を上げる(メモリの代わりに計算で制約される)ための方法が、データをミニバッチで処理することです。これはメモリ処理をいくらか避けることが可能で、またGPUは巨大な行列を並列的に処理するのに優れています。
しかし、バッチサイズを上げ過ぎると学習アルゴリズムに悪影響を及ぼし始め、収束が遅くなってしまいます。最前の結果と最短の時間を得るために、良いバランスを見つけ出すことが重要です。
18. 反対の例での学習
最近判明したことなのですが、ニューラルネットワークは反対の例によって容易に惑わされてしまうことが分かってきました。以下の例では、左の画像は正しく金魚として分類されます。しかし、真ん中の画像のノイズのパターンを適用してしまうと、右の画像がヒナギクとして分類されてしまうようになりました。この画像はAndrej Karpathyのブログ記事、 “Breaking Linear Classifiers on ImageNet” からのものであり、詳細はその記事で読むことができます。

このノイズパターンはランダムではなく、ネットワークを騙すように巧妙に計算されたものです。とはいえ、右の画像が明らかに金魚であってヒナギクでないことは変わりません。
アンサンブルモデル、複数サッケード後の投票、教師なし前学習などの戦略ではこの問題に対処できません。強い正規化を適用することは助けになりますが、それも精度がノイズパターンに影響される前のクリーンなデータで行わなければいけません。
Ian Goodfellow氏は、こういった反対例の学習についてのアイデアについて講演しました。こういう例はトレーニングセットに対して自動的に生成・追加することができます。反対例に適応した学習を行うことで、そういった例を含むデータセットのみならずクリーンなデータセットに対しても精度が向上したことを示すのが以下の図です。
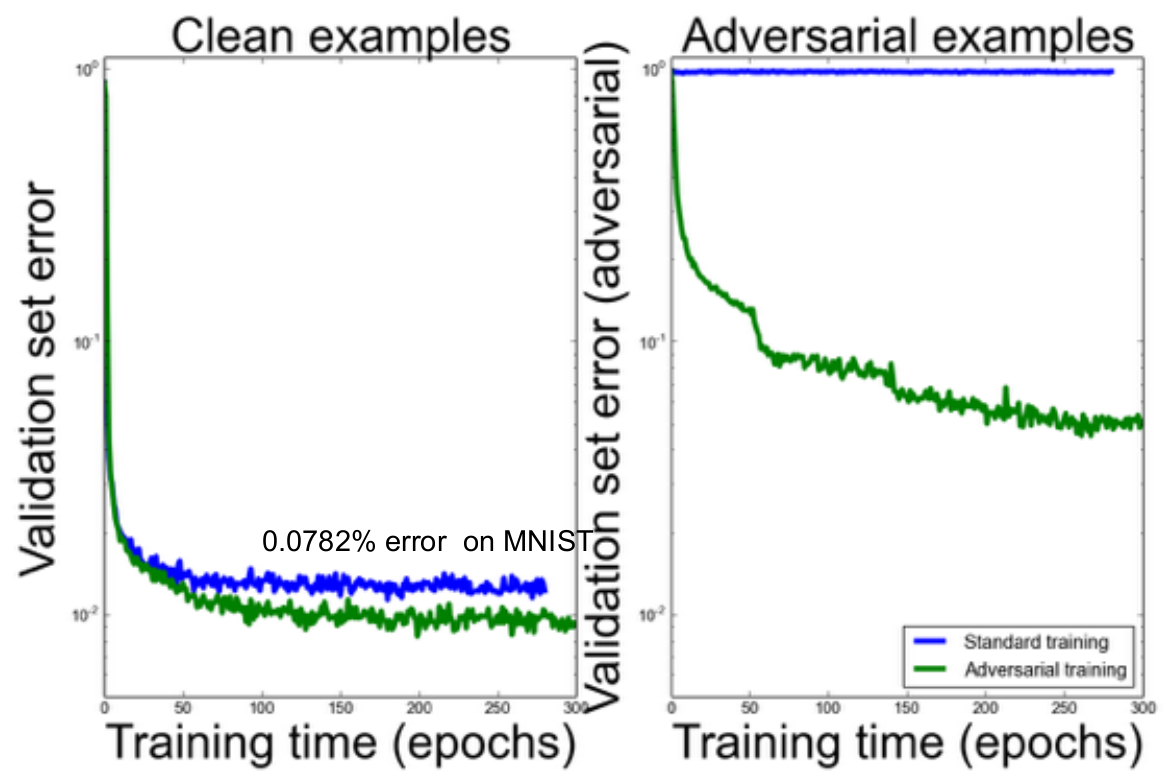
結局、オリジナル画像から予想される分布と生成された反対例から予想される分布について、その間のカルバック・ライブラー情報量にペナルティを与えることでより精度が向上します。これにより、ネットワークがよりロバストになり、また似た画像を似た分類の分布として予想できるように最適化できるのです。
19. 全ては言語のモデリング
Phil Blunsom氏の講演では、ほとんどすべてのNLPは言語モデルとして構造化できるという話をしてしました。インプットとアウトプットを連鎖的に繋ぎ、配列全体の確率を予測しようとすることでこれを行うことができます。
翻訳:
P(Les chiens aiment les os || Dogs love bones)
質問への回答:
P(What do dogs love? || bones .)
会話:
P(How are you? || Fine thanks. And you?)
下2つについては、加えて世界の知識の条件が必要となります。第二の部分については言葉である必要がありませんが、ラベルであったり、依存関係などのように構造化されたアウトプットである必要があります。
20. 統計的機械翻訳の始まりは粗雑だった
Frederick Jelinek氏とIBMのチームが統計的機械翻訳についての最初の論文を1988年のCOLINGに投稿したとき、以下のような匿名のレビューを受けました。
著者の言及通り、機械翻訳に対する統計的(情報理論的)なアプローチは、1949年という早さでWeaverが言及して認知されている。しかし、1950年には一般に誤りだったとして認識されるようになった(Hutchins, MT – Past, Present, Future, Ellis Horwood, 1986, p. 30ffおよびその参考文献)。コンピューターの未熟なパワーは科学ではなく、この論文はCOLINGの範囲外にある。
21. ニューラル機械翻訳の現状
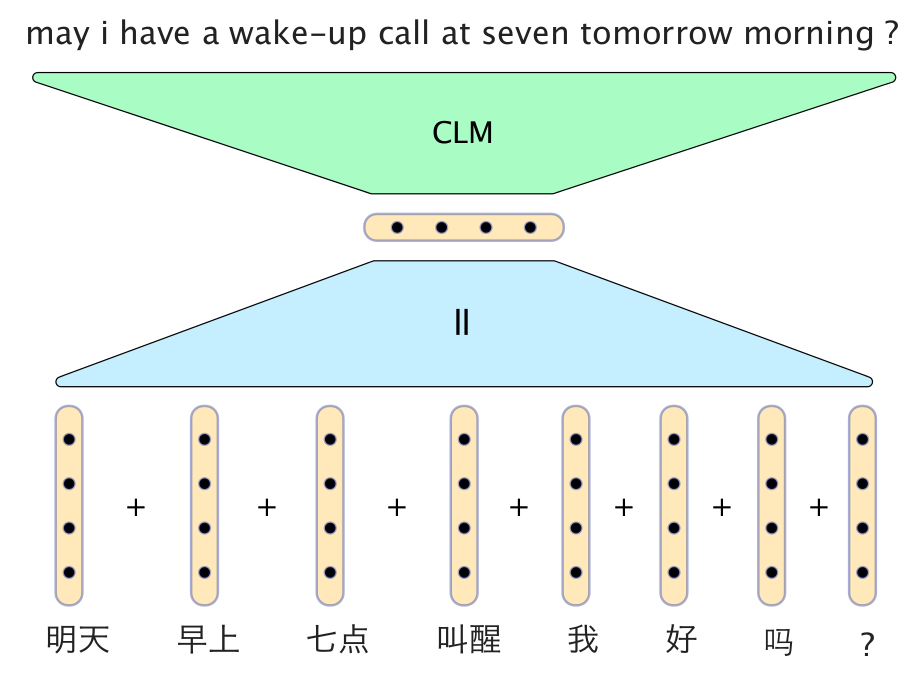
とてもシンプルなニューラルモデルが驚くほどよい結果を残しています。Phil Blunsom氏のスライドの、中国語から英語への翻訳の例が以下です。
このモデルでは、中国語の単語のベクトルを単純に足し合わせることで文のベクトルにしています。デコーダーは、生成された最新の2つの英単語のベクトルとともに文ベクトルを入力にとる条件的言語モデルで、翻訳の次の単語を生成します。
しかし、ニューラルモデルはまだ伝統的な機械翻訳システムを上回る成果を出していません。かなり近いところまでは来ていますが。以下が、Sutskeverらによる2014年の論文、 “Sequence to Sequence Learning with Neural Networks” からの結果です。
| モデル | BLEUスコア |
|---|---|
| Baseline | 33.30 |
| Best WMT’14 result | 37.0 |
| Scoring with 5 LSTMs | 36.5 |
| Oracle (upper bound) | ∼45 |
追記: @stanfordnlp が指摘してくれたのですが、いくつかの最新の結果ではニューラルモデルが最新の伝統的な機械翻訳システムよりいい結果を出したとのことです。 “ Effective Approaches to Attention-based Neural Machine Translation ” (Luong et. al., 2015)をご覧ください。
22. MetaMind分類器のデモ
Richard Socher氏は、画像をアップロードすることにより学習させられるMetaMindの 画像分類器のデモ をしてくれました。分類器にエジソンとアインシュタイン(テスラの画像は十分に見つけられませんでした)の画像で学習させました。それぞれの分類に5個の画像例を使い、それぞれの人物の他の画像を用いてテストしましたが、上手く機能しているようでした。
23. 勾配更新の最適化
Mark Schmidt氏の2つのプレゼンテーションは、異なるシナリオでの数値最適化に関するものでした。
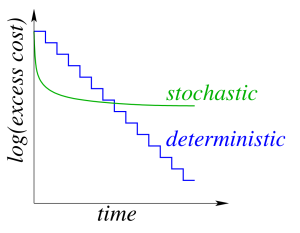
決定論的 勾配法では、データセット全体に対して勾配を計算して更新します。繰り返しのコストはデータセットのサイズに比例します。
確率論的 勾配法では、1つのデータポイントに対して勾配を計算して更新します。繰り返しのコストはデータセットのサイズに依存しません。
確率論的勾配法では各繰り返しは断然速いのですが、ネットワークをトレーニングするために必要な繰り返しの回数は多くなります。以下のグラフがそれを示します。
両者のうちのベストを得るために、バッチングを利用します。より具体的には、データセットのうち1つに対して確率論的勾配法を用いて正しい勾配方向を算出し、バッチサイズを上げ始めます。バッチサイズが大きくなるにつれて勾配の誤差は減っていきますが、繰り返しのコストは再びデータセットのサイズに依存してくるようになります。
確率論的平均勾配(Stochastic Average Gradient, SAG)はこの方式をとる手法で、繰り返しごとに1つの勾配を線形に増やしていきます。全てのデータポイントについての勾配の更新を記憶する必要があり、それに従いメモリの消費量が大きくなってしまうため、残念ながら巨大なニューラルネットワークには適しません。確率的分散減少勾配(Stochastic Variance-Reduced Gradient, SVRG)はこのメモリコストを減らす手法で、繰り返しごとに2つの勾配のみを計算するものです(加えて、時により全ての勾配を用います)。
Mark氏は生徒に対し、彼が実装した多くの最適化手法(AdaGrad, モーメンタム, SAGなど)について話しました。「ブラックボックス的なニューラルネットワークに対してはどういう手法を用いるのか」と生徒に質問された際には、彼は2つの手法を用いると答えました。一つは Streaming SVRG (Frostig et al., 2015)、もう一つはまだ論文化していないもの、とのことでした。
24. Theanoのプロファイリング
THEANO_FLAGSに“profile=True”を書き込むと、プログラムを解析し、各処理のうちどこに多くの時間が割かれているかを見せてくれます。ボトルネックを見つけるのに非常に便利です。
25. 反例ネット・フレームワーク
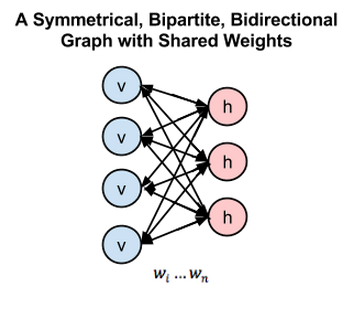
Ian Goodfellow氏の反対例に関する講演のあと、Yoshua Bengio氏が「それぞれ競い合う2つのシステム」について話しました。
システムDは分類システムで、実データと人工的なデータを分類することを目的としたものです。
システムGは生成システムで、システムDが誤って実データと認識してしまうように人工的にデータを生成することを目的としています。
片方を訓練することで、もう片方はより高精度にならなければなりません。実際にこれは上手く機能していますが、システムDがシステムGについていくためにはその訓練のステップ幅を極めて小さくしなければなりません。以下が“ Deep Generative Image Models using a Laplacian Pyramid of Adversarial Networks ”からの例で、教会の画像を生成するモデルのものです。
26. arXiv.org のナンバリング
arXivのナンバリングは、投稿年月と投稿された順番からなります。1508.03854 とナンバリングされた論文は、2015年に投稿された3854番目の論文ということになります。知れて良かったです。
株式会社リクルート プロダクト統括本部 プロダクト開発統括室 グループマネジャー 株式会社ニジボックス デベロップメント室 室長 Node.js 日本ユーザーグループ代表
- X: @yosuke_furukawa
- Github: yosuke-furukawa