世界を考察する新しい方法を手に入れたときの感覚が大好きです。特に好きなのは、いずれ具体的なコンセプトに形を変えるボンヤリとした考えがあるときです。情報理論は、その最たる例です。

情報理論は、多くの物事を説明するための正確な言葉を与えてくれます。自分はどのくらい理解できていないのか？質問Aの答えを知ることが、質問Bを答えるのにどのくらい役立つのか？ある種の信念が他の信念とどの程度似ているのか？こういうことに対し、若くて未熟なころから自分なりの考えがありましたが、情報理論に出会って正確で強固な考えとしてはっきりと固まりました。その考えは、桁外れの、例えばデータの圧縮から量子物理学や機械学習、さらにはその間に広がる数多くの分野に応用が利くものです。

残念なことに、情報理論は少々威嚇的に見えてしまうのですが、そう断定すべき根拠は全くないと思います。実際、情報理論の多くの重要な概念は完全に視覚的に説明できるのです。

確率分布の視覚化

情報理論に挑戦する前に、簡単な確率分布を視覚化する方法を考えましょう。視覚化は後段でも必要なので、今やっておくと役立つでしょう。おまけに、確率を視覚化する方法はそれ自体が役に立ちます！

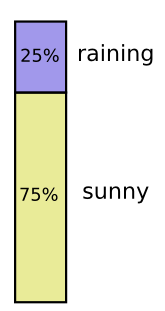
私はカリフォルニアにいます。雨が降ることもありますが、ほとんどの日が晴れです！晴れの日が75%だとしましょう。これを図にするのは簡単です。

Ｔシャツを着る日がほとんどですが、コートを着ることもあります。コートを着るのが38%としましょう。これも図にするのは簡単です！

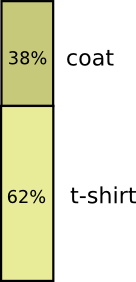
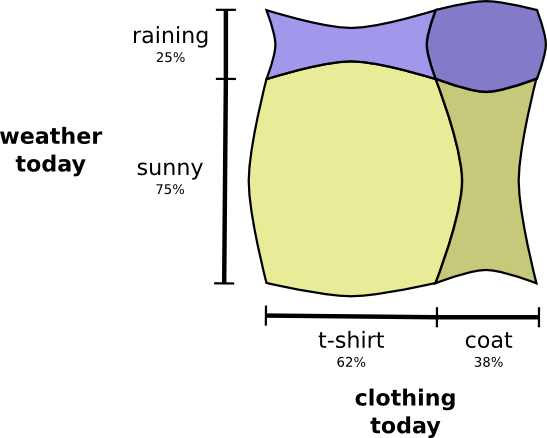
上の2つを同時に視覚化するとどうなるでしょう？お互いが干渉しない、つまり、いわゆる独立であれば、とても簡単です。例えば、今日Ｔシャツを着るかレインコートを着るかは、実際には来週の天気に関係しません。これは、1つの軸に1つの変数、別の軸に別の変数を使って描くことができます。

注釈：
（縦軸）来週の天候／雨25％、晴れ75％
（横軸）今日の服装／Ｔシャツ62％、コート38％

縦軸側も横軸側も直線が貫いていることに注目してください。 独立とはこういうことなのです！ ^(1) 私がコートを着る確率は、この先1週間で雨が降るだろうという事象に対応して変化するものではありません。言い換えると、「私がコートを着て、かつ来週雨が降る」という確率は、「私がコートを着る」確率に「来週雨が降る」確率を掛け合わせたものです。両者に相互の関係性はありません。

変数が相互に関係する場合には、変数の特定の組み合わせの確率が増加し、別に組み合わせの確率が減少します。変数に相互関係があると、「私がコートを着て、かつ雨が降る」という確率が増加し、相互作用がない場合に比べてお互いに確率を高め合います。「雨の日に私がコートを着る」確率は、ある日に私がコートを着て、かつ他の任意の日に雨が降る確率よりも、高くなるのです。

視覚化すると、確率の増加で膨張するマス目もありますし、同時に起こりそうもない事象の組み合わせ故に縮小するマス目もあります。

これはいくらかクールに見えますが、何が起きているのかを理解するのには全く役立ちません。

全体よりも、天候という1つの変数に注目してみましょう。晴れと雨の確率がどのくらいかは分かっています。いずれの場合も、 条件付き確率 を見ることができます。晴れた日にＴシャツを着る確率はどのくらいでしょうか？雨の日にコートを着る確率はどうしょうか？

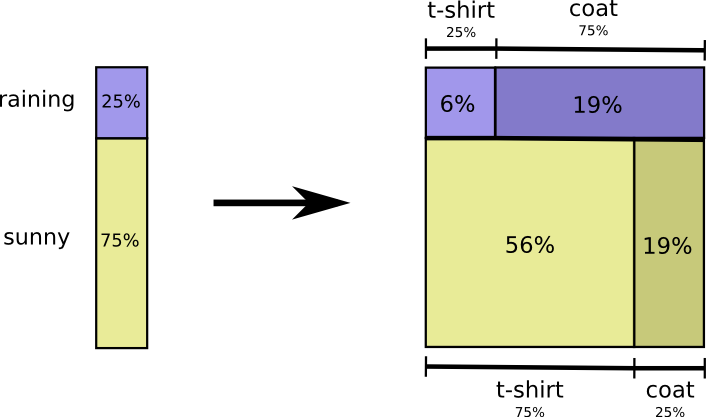
「雨が降る」可能性は25%です。もし雨が降れば、私がコートを着る可能性は75%です。ですから、「雨が降り、かつ私がコートを着る」確率は、25%と75%を掛け合わせて、約19%になります。「雨が降り、かつ私がコートを着る」確率は、「雨が降る」確率と「雨が降った場合において、コートを着る」確率との掛け算になります。このことを以下のように書きます。

\[p(\text{rain}, \text{coat}) = p(\text{rain}) \cdot p(\text{coat} ~|~ \text{rain})\]

この式は、確率論の最も基本的な恒等式の1つの事例です。

\[p(x,y) = p(x)\cdot p(y|x)\]

分布を2つの積に分割して、 因数分解しています 。まず1つの変数、例えば天候が、ある特定の値になる確率を見てみます。そして次に、別の変数、例えば私の服装が、1つ目の変数の条件によって、ある特定の値を持つ確率を見ます。

初めにどちらの変数を選択するのかは任意です。「服装に着目することから始めて、その条件により天候を考える」というのも難しさは変わりません。これはあまり直観的ではないと感じるかもしれません。というのも、「天候が、私が何を着るかに影響を与える」という因果関係はあっても、逆は因果関係ではないからです。しかし、それでもうまく機能します。

一例を見てみましょう。無作為にある1日を選んだ時に、私がコートを着る可能性を38%とします。もし私がコートを着ていると分かった場合に、雨が降っている可能性はどの程度でしょうか。そうですね、晴れの日よりも雨の日の方がコート着る可能性は高いように思います。しかし、カリフォルニアでは雨はかなり珍しいので、雨が降っている可能性は50%と導き出します。ですから、雨が降っていてかつ私がコートを着ている確率は、私がコートを着ている確率（38%）と、私がコートを着ていて雨が降っている確率（50%）を掛け合わせた約19%になります。

\[p(\text{rain}, \text{coat}) = p(\text{coat}) \cdot p(\text{rain} ~|~ \text{coat})\]

これで、厳密に同一な確率分布を視覚化する2つ目の方法が得られました。

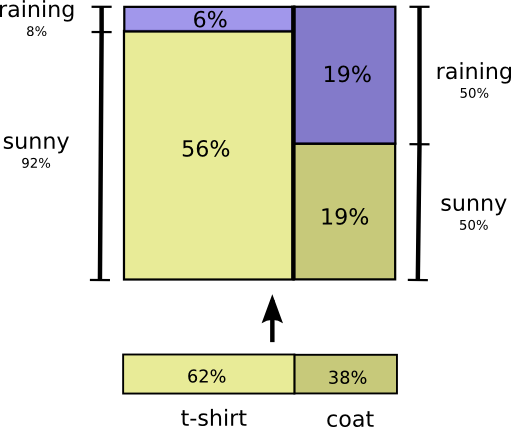
注釈：
（左縦軸）雨8％、晴れ92％
（右縦軸）雨50％、晴れ50％
（横軸）Ｔシャツ62％、コート38％*

前出の図とは、項目名がわずかに異なる意味を持っていることに注意してください。今回は、Tシャツとコートは 周辺確率 であり、私が衣服を着ている確率ですから天候は考慮に入れません。これに対して、雨と晴れという項目名があります。これはそれぞれ、私がTシャツを着ている場合、コートを着ている場合の確率に対するものです。

（ベイズの定理について聞いたことがあるかもしれません。もしよければ、この定理を、確率分布を示すこれらの2つの異なるやり方を変換するための方法と思ってください）

余談、シンプソンのパラドックス

実際に確率分布を視覚化するためのこれらの手法は、お役にたちましたか？そうだといいのですが。情報理論を視覚化するためにこの手法を使うのはもう少し先のことになります。それでは少し脇道にそれて、シンプソンのパラドックスを探求するために、この手法を使ってみたいと思います。シンプソンのパラドックスは、極めて直感的に分かりづらい統計的状況です。直感的なレベルで理解することは本当に難しいものです。Michael Nielsenは、このパラドックスを説明するための異なったやり方を調査した、素晴らしいエッセイ 説明の再考 を書きました。前のセクションで詳しく述べた手法を使って、自分で説明をしてみたいと思います。

腎結石に対する2つの治療法が調査対象です。患者の半数に治療Aを施し、残りの半数に治療Bを施します。治療Bを受けた患者の方が、治療Aを受けた患者よりも長生きしているようです。

注釈：
（縦軸）生存者率
（横軸）治療A 50%、治療B 50%

しかし腎結石が小さい患者は、治療Aを受けていても、より長生きしているようでした。腎結石が大きい患者も、治療Aを受けていれば、長生きしているようなのです！一体どうなっているのでしょう？

問題の核心は、研究は正しく無作為抽出されなかったということです。治療Aを受けた患者には大きな腎結石がある可能性が高く、一方治療Bを受けた患者には小さな腎結石がある可能性が高かったのです。

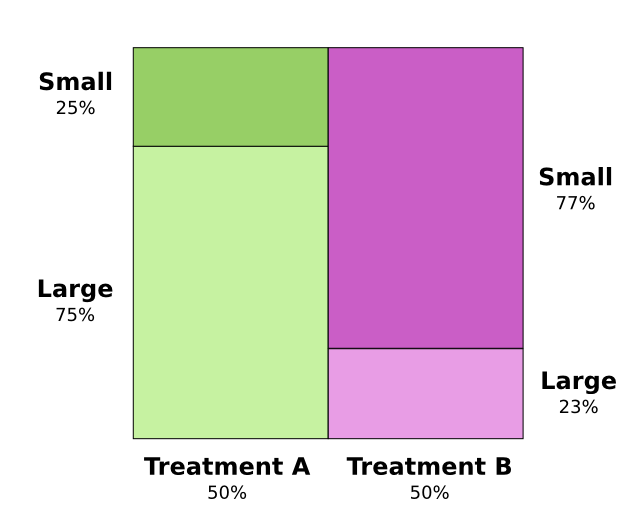
注釈：
（左縦軸）小25％、大75％
（右縦軸）小77％、大23％
（横軸）治療A50％、治療B50％

結局のところ一般的に、腎結石が小さい患者の方が、はるかに長生きするようです。

このことをもっと良く理解するために、前の2つの図を合体させてみましょう。その結果は生存者率を腎結石の大小で分割した3次元のグラフになります

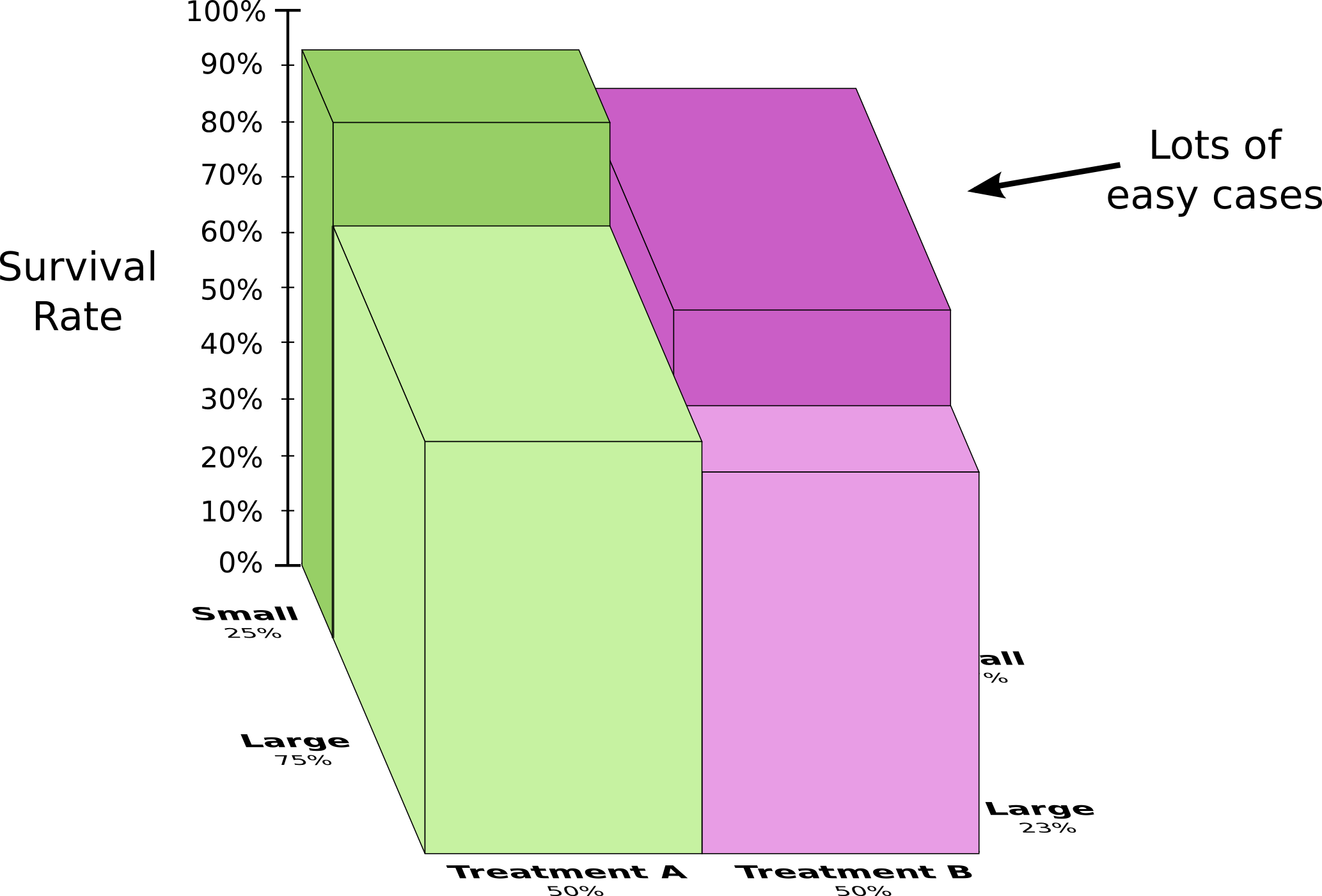
注釈：
（縦軸）生存者率
（左奥行軸）小25％、大75％
（右奥行軸）小77％、大23％*
（横軸）治療A50％、治療B50％
Lots of easy cases／多くの軽微な症例*

小さい腎結石と大きい腎結石の両方のケースを考慮すると、治療Aは治療Bより有効だということが 分かりました 。治療Bを受けた患者は最初から長生きする可能性が高かったので、より有効なのは治療Bであるように見えたのです！

コード

確率を視覚化する方法が分かったところで、情報理論の話に入りましょう。

ここでは私の想像上の友人であるBobの話をしたいと思います。Bobは動物を愛しており、いつも動物の話ばかりしています。実際のところ、彼が口にするのは”犬”、”猫”、”魚”、”鳥”という4つの単語だけです。

架空の存在ではありますが、このBobが数週間前にオーストラリアに引っ越しました。そしてさらに、彼はバイナリコードだけで連絡を取ると決めたのです。Bobからの（想像上の）メッセージは次のようなものです。

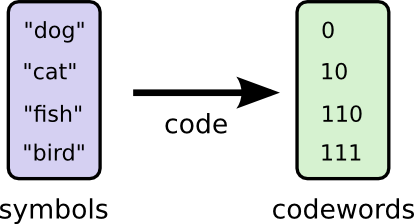
連絡を取るために、Bobと私はコードを決めなければいけません。単語をビットの並びにマッピングするのです。

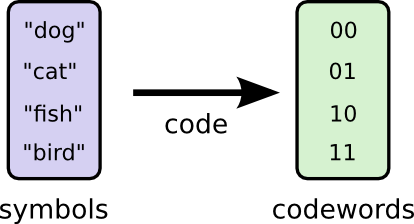
メッセージを送る際にBobはそれぞれのシンボル（単語）を対応するコードワードに置き換えます。そして、それらを連結させてエンコードされた文字列の形式にします。

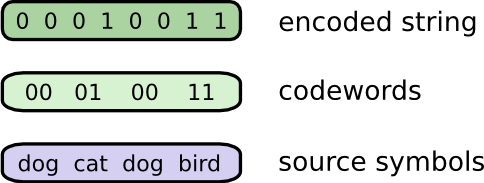
注釈：
エンコードされた文字列
コードワード
元のシンボル

可変長コード

残念なことに、架空のオーストラリアの通信サービスは高くつきます。私はBobからメッセージ受け取る度、1ビットごとに5ドルも支払わなければいけません。Bobは話好きだということをお伝えしていたでしょうか？ 破産を防ぐために、Bobと私はメッセージの長さを平均的に短くする方法を探ることにしました。

Bobは4つ単語を同じ頻度で口にするわけではありません。彼は犬が大好きで、しょっちゅう犬の話をしています。彼の犬が追い掛け回している猫についてなど、時々は違う動物の話をすることもありますが、ほとんどの場合が犬の話です。彼が口にする単語の頻度をグラフにしました。

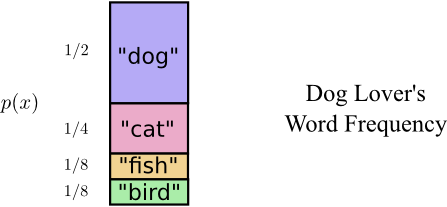
注釈：犬好きが口にする単語の頻度

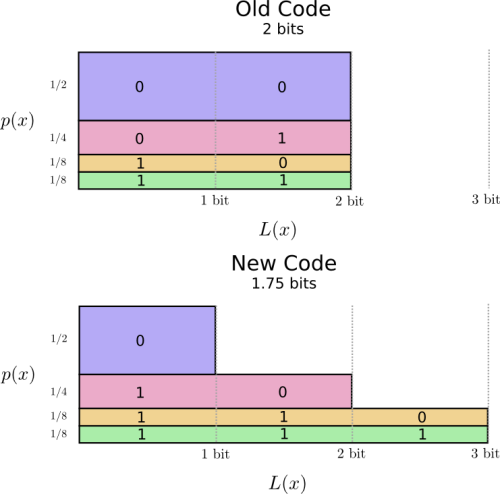
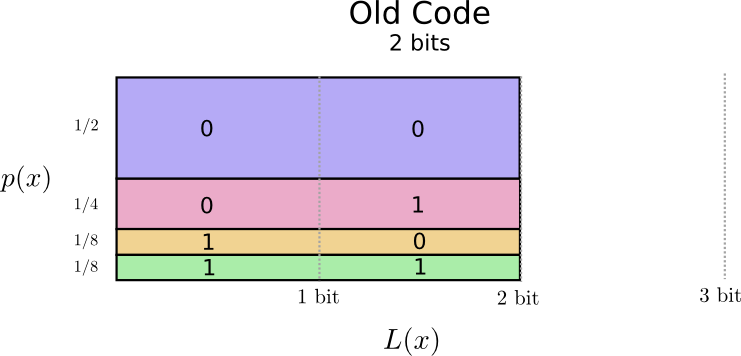
解決策が見えてきそうです。私たちの古いコードでは、頻度に関わらず2ビットのコードワードを使用します。

これを視覚化するいい方法があります。次の図では、それぞれの単語の確率 \(p(x)\) を縦軸に、対応するコードワードの長さ \(L(x)\) を横軸に表しました。この面積は私たちが送信するコードワードの長さ、つまり2ビットということに注目してください。

恐らく私たちは賢い方法で、頻度の高い単語が最も短いという可変長コードを作ることができるでしょう。問題となるのはコードワード間の相互作用です。短いコードを作ると、長いコードも出来てしまいます。メッセージの長さを最小限に抑えるためには全てのコードワードが短いことが理想的なのですが、頻度の高い単語のコードを短くすることが最も重要です。結果として、頻度の高い単語（”犬”）のコードワードは短く、頻度の低い単語（”鳥”）のコードワードは長くなります。

もう一度、視覚化してみましょう。最も頻度の高いコードワードは短く、頻度の低い単語のコードワードは長くなっていますね。この結果は図において、古いコードよりも小さい面積で表されます。これは、より小さいと予測されるコードワードの長さに対応します。コードワードの長さは平均で1.75ビットになりました！

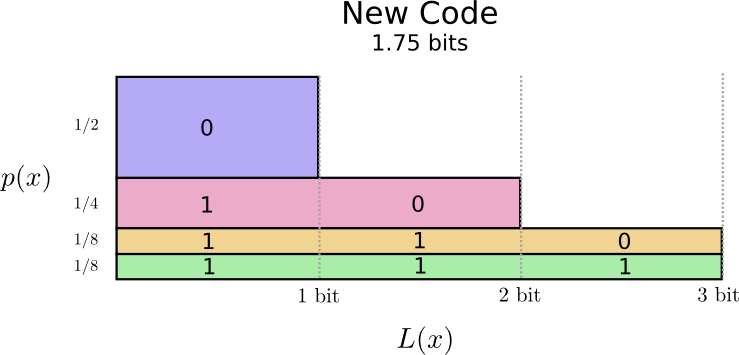
（なぜコードワードとして1を単独で使用しないのかと不思議に思われることでしょう。残念なことに、そうしてしまうと、エンコードされた文字列をデコードした際に曖昧さを引き起こすのです。これについてはあとで説明します）

さて、これが最良のコードとなりました。この分布では、コードワードの長さの平均が1.75ビット以下になるコードはありません。

ここには単純に本質的な限界が存在します。伝えたい単語や、この分布から得られた結果をやりとりするためには、少なくとも平均で1.75ビットが必要です。私たちのコードがどれほど優秀でも、メッセージの長さをこれより短くすることは不可能です。この本質的な限界を、分布のエントロピーと呼びます。これについては、あとでより詳しく見ていきましょう。

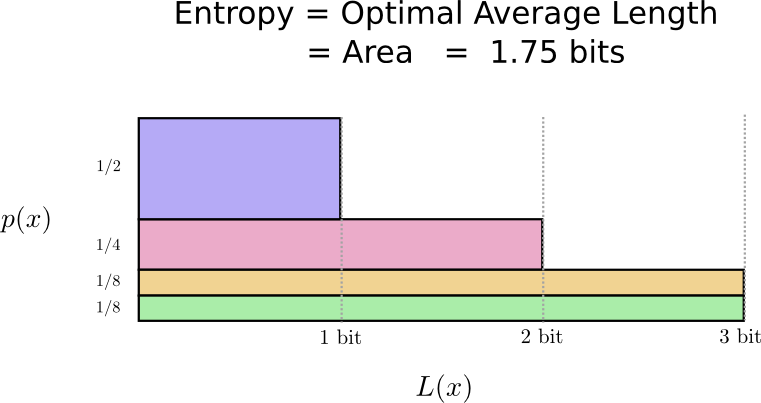
注釈：
エントロピー＝最適な平均の長さ＝面積＝1.75ビット

この制限を理解するには、あるコードワードを短くすると、それ以外のコードワードが長くなるという相互作用を理解することが肝心です。一度これを理解してしまえば、最良のコードがどんなものか分かるようになるでしょう。