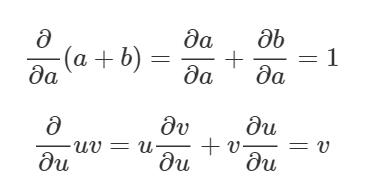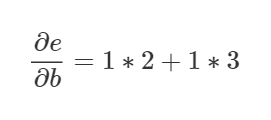はじめに

バックプロパゲーションとは、ディープモデルの学習を計算可能にしてくれる重要なアルゴリズムです。最近のニューラルネットワークではバックプロパゲーション (誤差逆伝播法) を使うことで、最急降下法による学習が愚直な実装と比べて1000万倍速くなります。
例えば，バックプロパゲーションでの学習に1週間しかかからないのに対して、愚直な実装では20万年かかる計算になります。

ディープラーニングでの使用以外にも、バックプロパゲーションはさまざまな分野で使えるとても便利な計算ツールです。それぞれで呼ばれる名称は違うのですが、天気予報から、数値的安定性を分析する時にまで多岐にわたり使用できます。実際に、このアルゴリズムは、いろいろな分野で少なくとも20回は再開発されています（参照： Griewank（2010） ）。一般的な用途自体の名前は”リバースモード微分”といいます。

基本的に、この技術は微分の計算をスピードアップさせるものです。ディープラーニングだけではなく、さまざまな計算法の場面で、気軽に使える必要不可欠な方法です。

計算グラフ

計算グラフは数式を考える上でとてもいい手段です。例えば、 e = (a + b) * (b + 1) という数式があるとしましょう。これには3つの演算があります。加算が2つと、乗算が1つです。話を進めるために、追加で c と d という2つの変数を加えましょう。こうすれば、全ての関数の出力を変数と考えることになります。以下のように表せます。

c = a + b
d = b + 1
e = c * d

そして、入力変数に沿ってこれらの演算を節点にして計算グラフを作ります。ある節点の値が別の節点の入力となっていたら、矢印をそちらに向けてつなぎます。

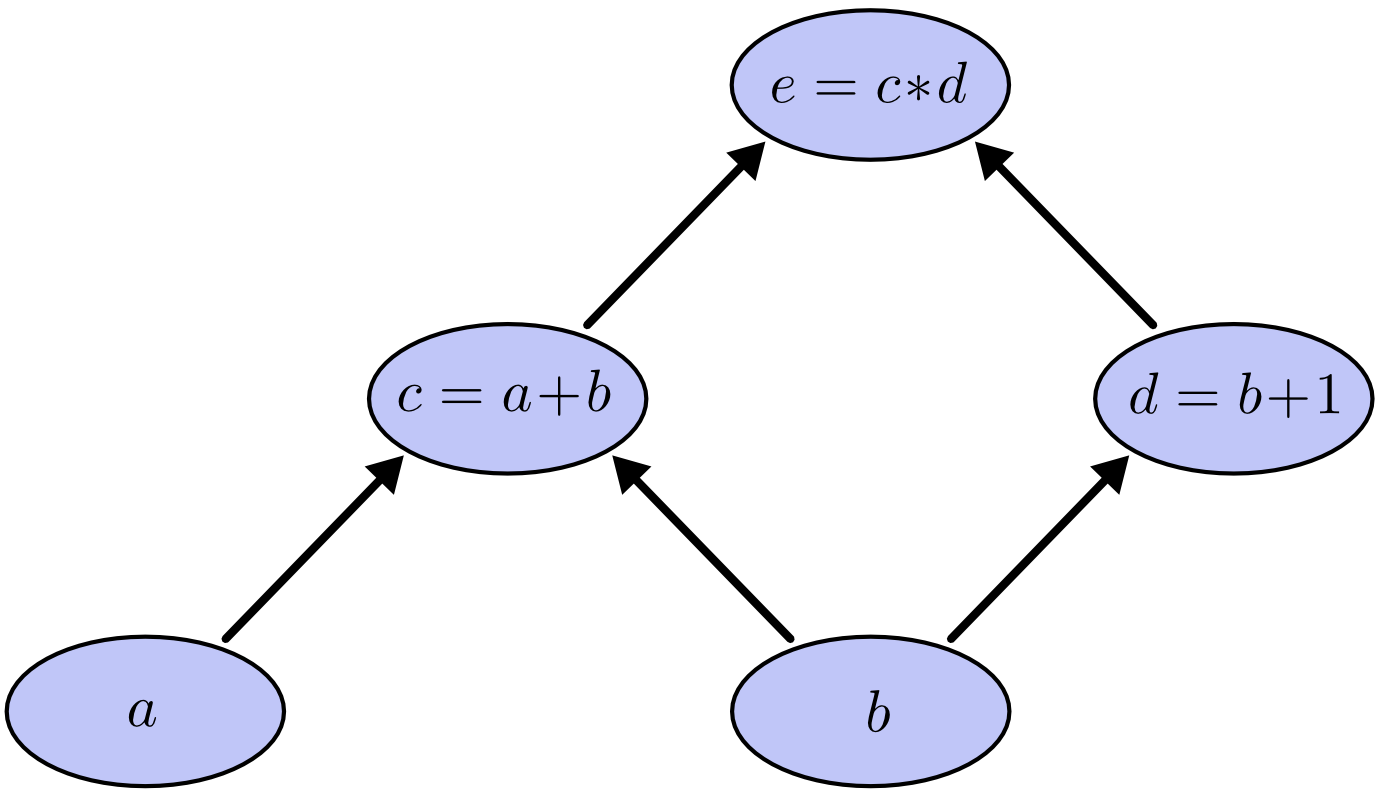
このようなグラフはコンピュータ・サイエンスの世界で関数型プログラミングの話になると常に登場してきます。依存性グラフやコールグラフの考え方ととても似ています。また、これは Theano という人気のあるディープラーニングのフレームワークと関わりのあるコアの抽象化概念でもあります。

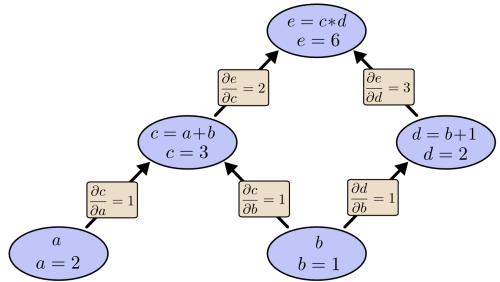
この式の値を求めるには、入力変数に特定の値を代入し、節点をグラフの下から上に計算していきます。例えば、 a = 2 、 b = 1 だとしましょう。

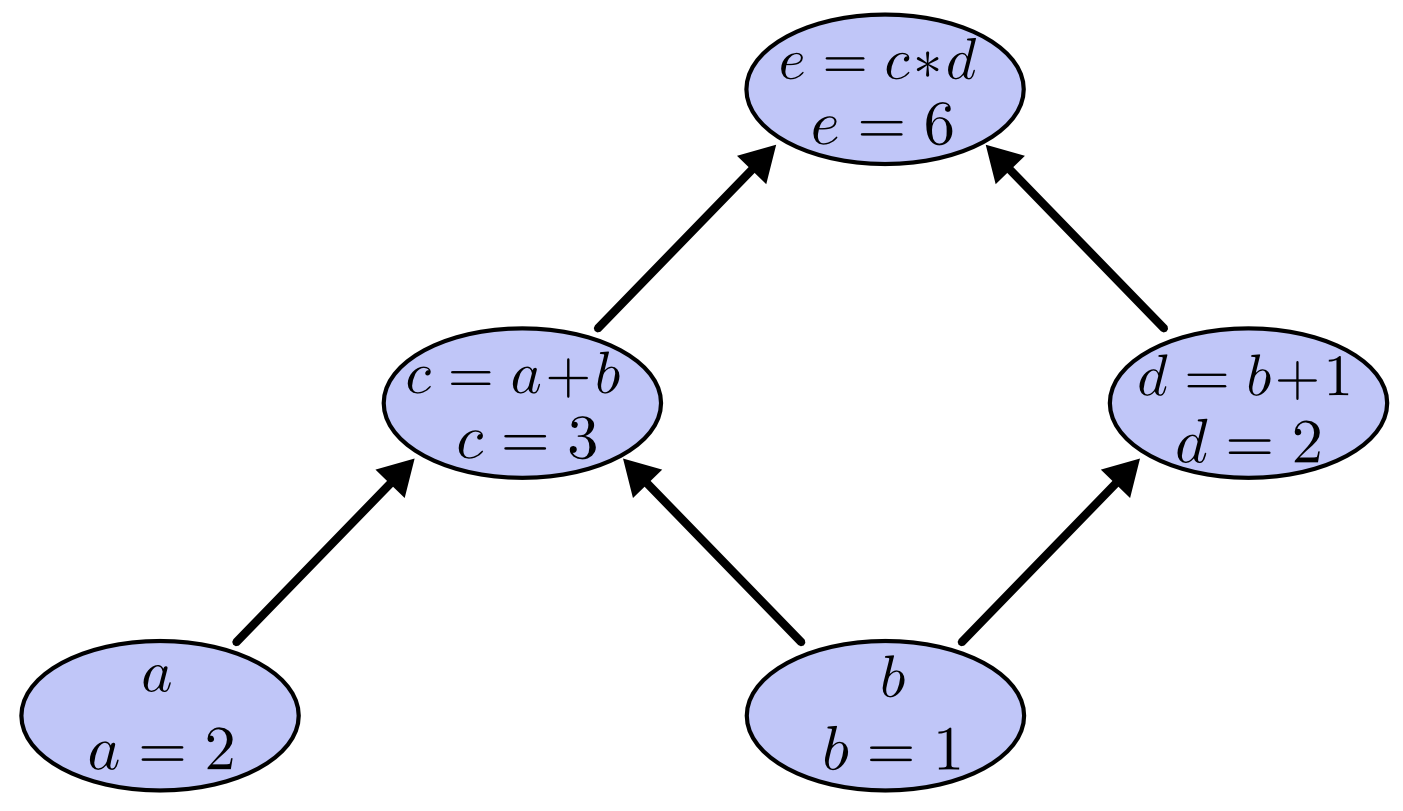
式の値は6となりました。

計算グラフの微分

計算グラフの微分を理解するには、辺の微分を理解するのがポイントです。もしaが直接的にcに作用するならば、どのようにcに作用があるのか探りたくなりますよね。もしaが少しでも変化すれば、cはどうやって変化していくのでしょうか。これを、aに対するcの偏微分と呼びます。

このグラフの偏微分の値を求めるには、 和の微分法則 と 積の微分法則 が必要になります。

以下のグラフは、微分係数がそれぞれの辺に書いてあります。

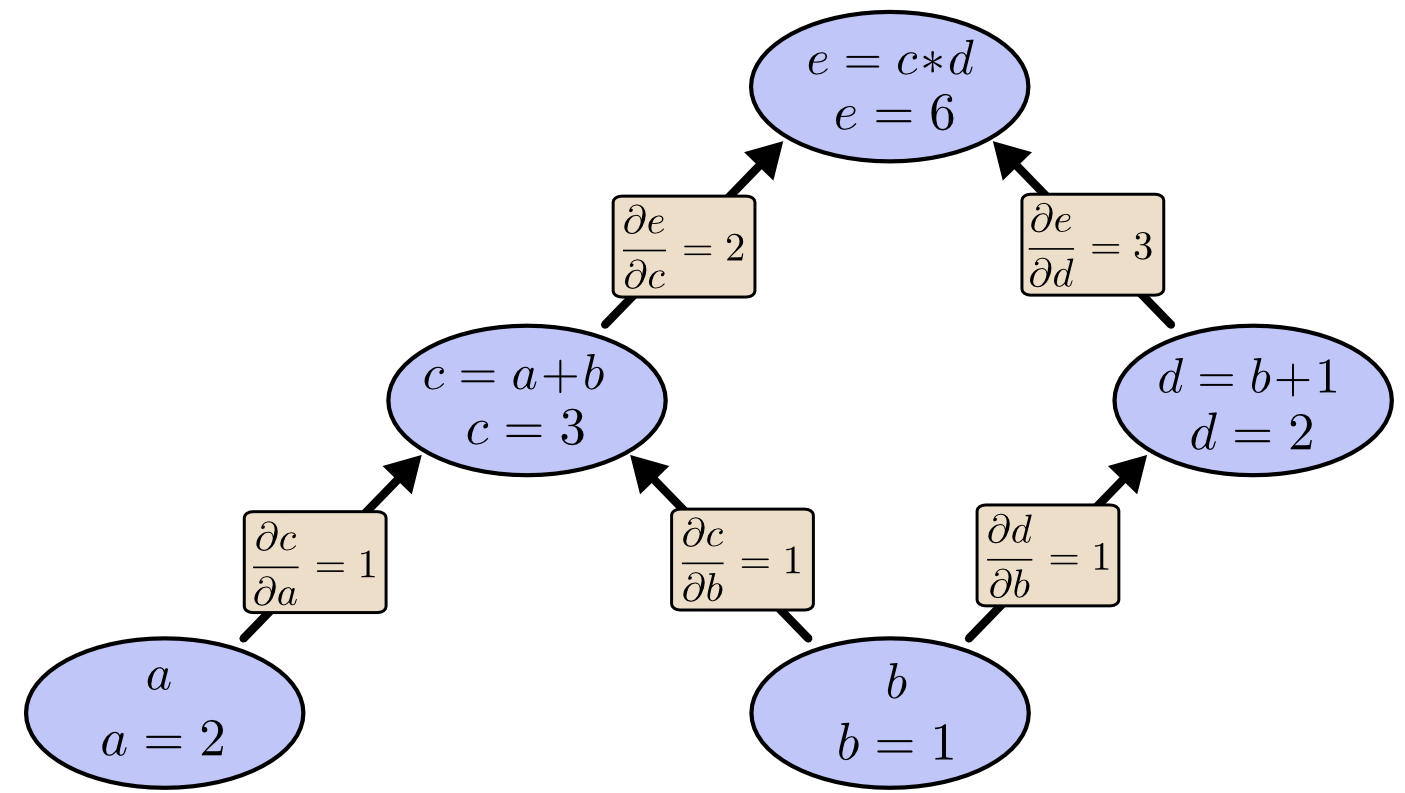
直接つながっていない節点同士の関係は、どのように理解すればよいでしょうか。理解するためには、aはどのようにeに作用しているのか考えてみましょう。もし1の速さでaが変化したら、cも同じように1の速さで変化します。次に、1の速さで変化するcは、2の速さでeに作用します。つまり、aに対するeは1*2の割合で変化することになります。

このグラフの原則では、ある節点から別の節点にいく道筋の全てのパターンを合計します。道筋のそれぞれの辺の微分係数を全て掛けるのです。例えば、bに対するeの微分係数を求めるには以下のような式になります。

これは、bがcを通してどのようにeに作用し、また、dを通してどのように作用したかによります。この”道筋の合計”の原則は単に、 多変数の連鎖律 の別の考え方と思ってください。

道筋を因数分解する

単に”道筋の合計”を行うことの問題は、道筋の数によって容易に組合せが爆発的に増加するということです。

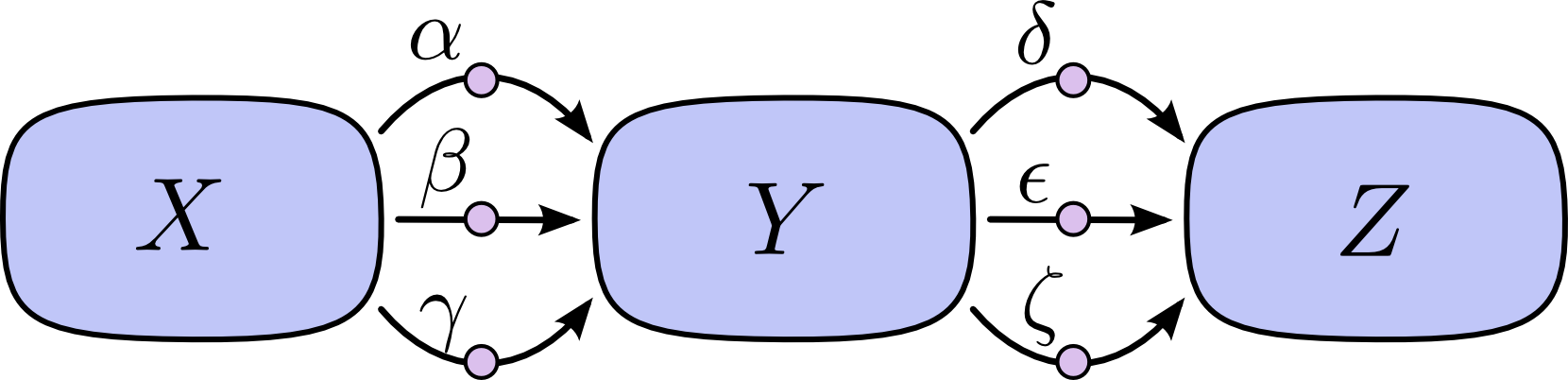
上の図では、XからYへの道筋は3つあり、さらにYからZに3つの道筋があります。全ての道筋を合計することで微分を求めようとすると、3∗3=9の道筋の和が必要です。

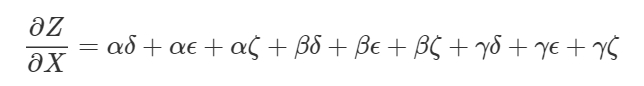
道筋は、上の図では9通りだけでしたが、グラフが複雑になれば、その数が飛躍的に増加するのは想像に難くありません。
そうした場合、単純に道筋を加算するよりも、それを因数分解した方がはるかに得策でしょう。

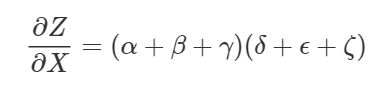
ここで使われるのが”フォワードモード微分”と”リバースモード微分”です。この2つは、道筋を因数分解することで効率的に合計を算出できるアルゴリズムで、明示的に全ての道筋を合計する代わりに各節点で道筋を1つに結合し、同じ和をより効率的に導き出します。実際のところ、両方のアルゴリズムでは厳密に1回、各辺を通ります。

フォワードモード微分はグラフへの入力で始まり、各節点で与えられた全ての道筋を合計しながら、終わりに向かって移動します。それぞれの道筋は、入力から節点への作用のしかたを表すものです。道筋を加算していくことで、入力が節点に与える全ての作用のしかたを得ることができます。それが微分係数です。

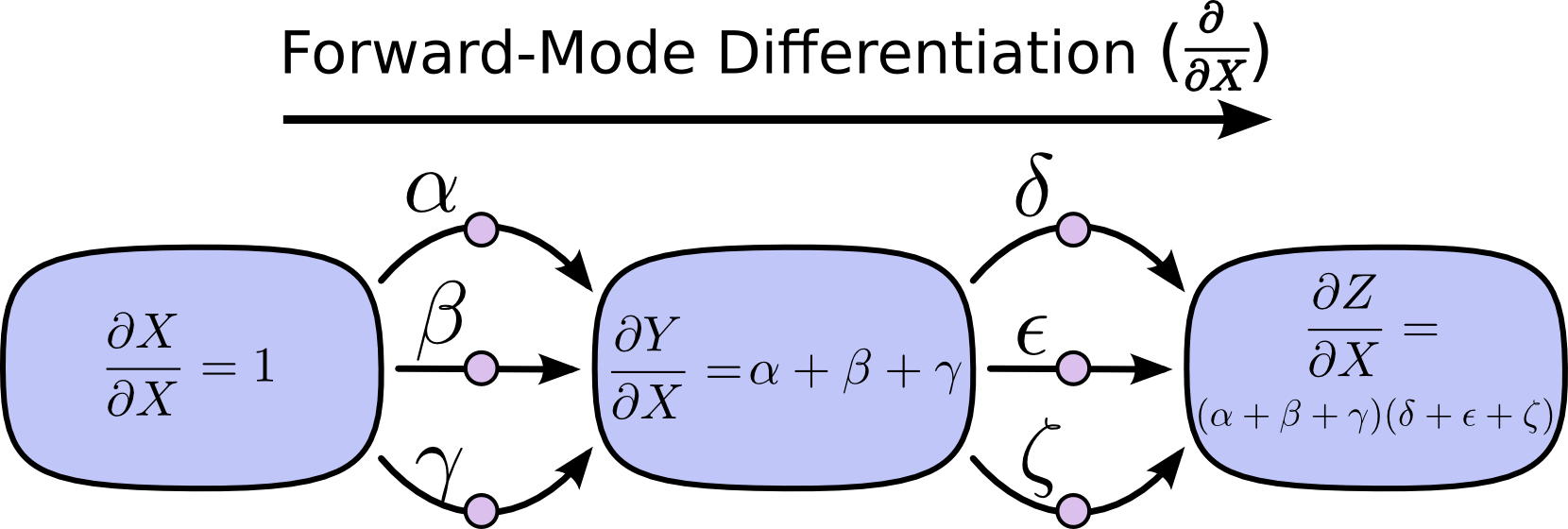
注釈：フォワードモード微分

グラフという点から見ると想像しにくいかもしれませんが、フォワードモード微分は、微積分を学ぶ際に自然に身に付くことに、とても近いのです。

リバースモード微分はそれとは逆で、グラフの出力から始まり、節点で発生した全ての道筋をマージしながら、先頭に向かって移動します。

注釈：リバースモード微分

ある入力がどのように各節点に作用するのかを追跡するのがフォワードモード微分だとすれば、各節点がある出力にどう作用するのかを追跡するのがリバースモード微分だと言えるでしょう。つまり、フォワードモード微分は $ \frac{\partial}{\partial X} $ 演算子を全ての節点に適用し、リバースモード微分は $ \frac{\partial Z}{\partial} $ 演算子を全ての節点に適用しているというわけです。 ^(1)

計算の勝利

この時点で皆さんは、誰がリバースモード微分に関心を持つのか、と不思議に思われるかもしれません。確かに、フォワードモード微分と結果が同じ割には、ずいぶんおかしな方法に見えます。どんな利点があるのでしょうか。
ここで、再び最初の例を考えてみることにしましょう。

bから上がってフォワードモード微分すると、bに対する全ての節点の微分係数を得ることができます。

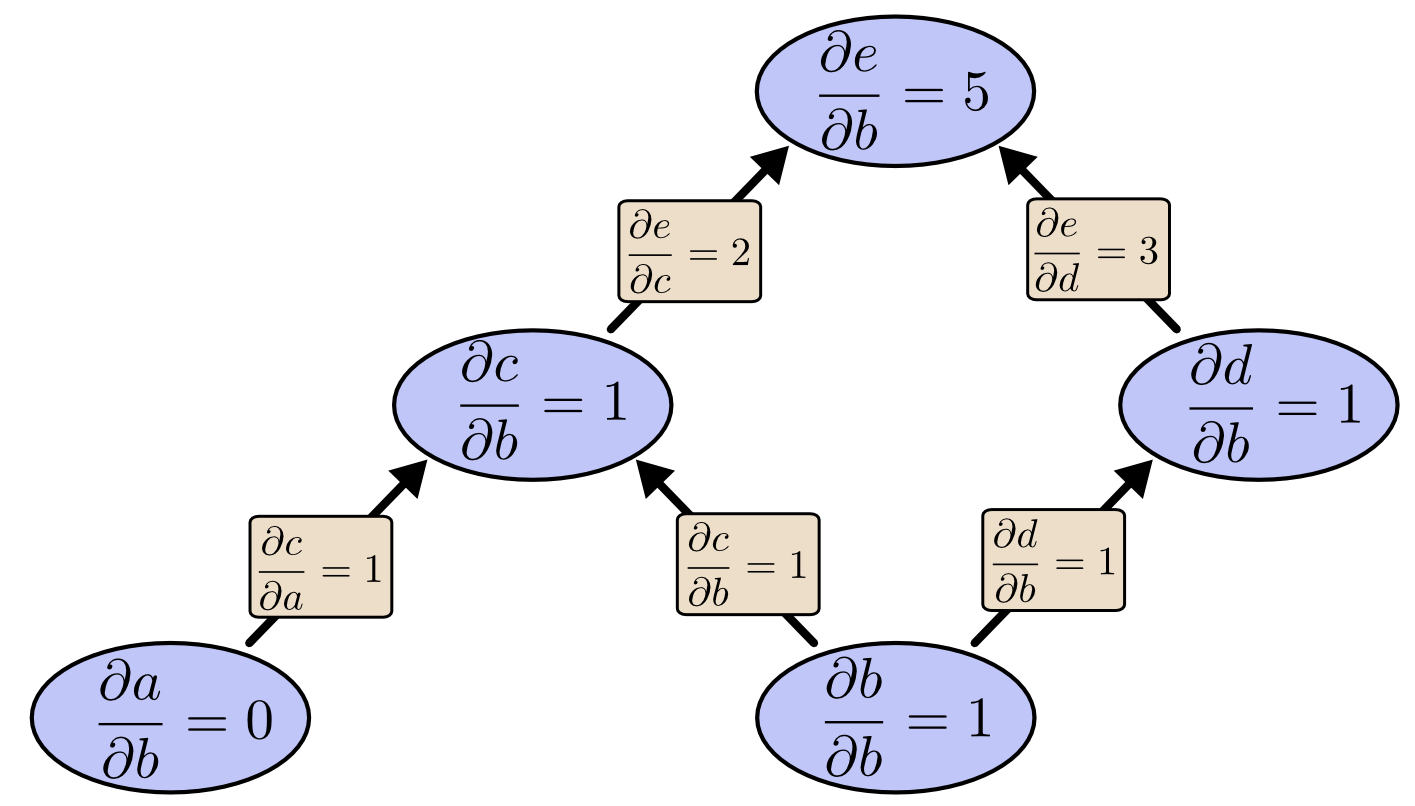
入力の1つに対する出力の微分係数である $ \frac{\partial e}{\partial b} $ を計算しました。

これを、eから下りてリバースモード微分するとどうなるでしょうか。以下のように、全ての節点に対するeの微分係数を得ることができます。

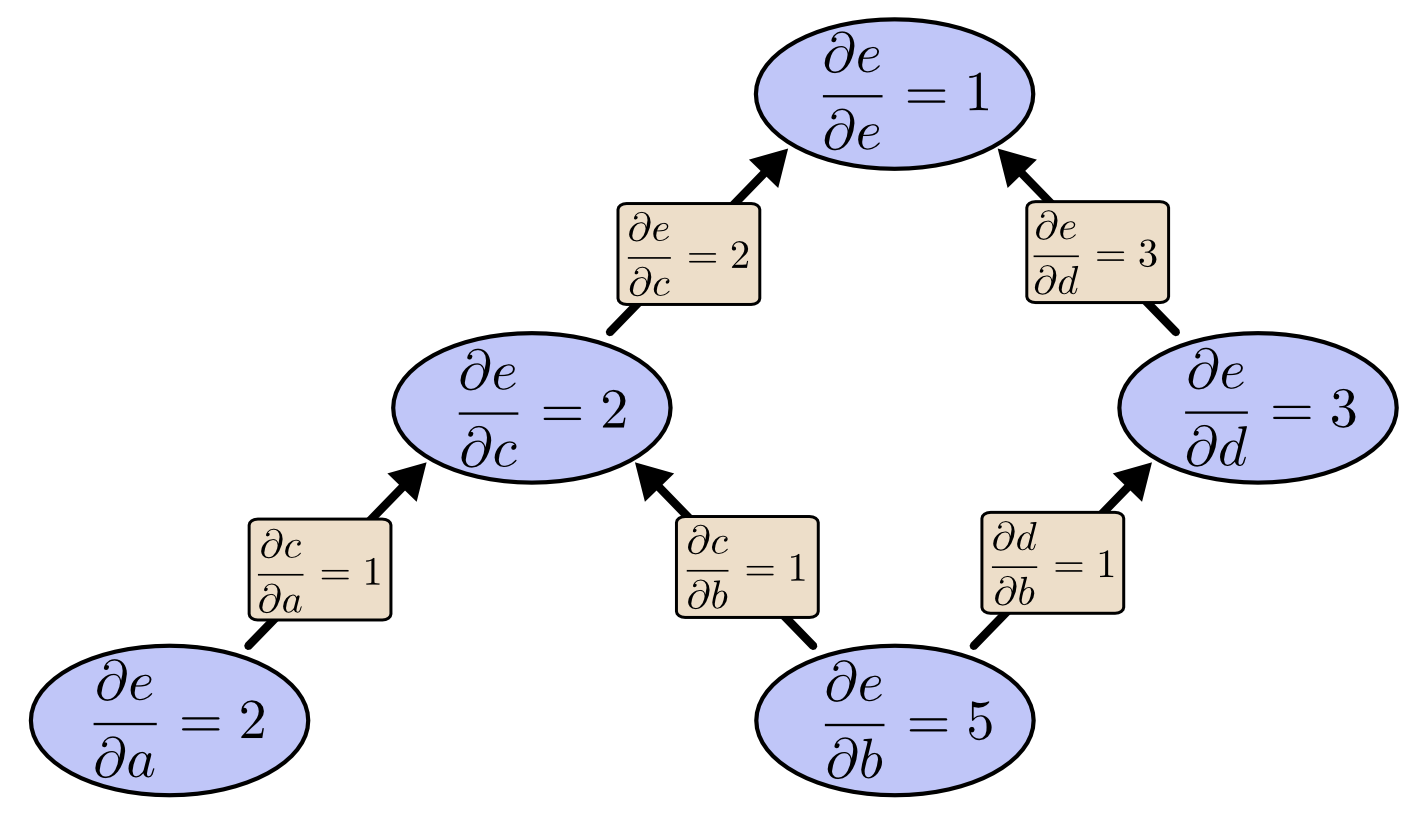
リバースモード微分で、全ての節点に対するeの微分係数を得られるということに言外の意味はなく、実際に 全ての節点 を意味しています。得ることができるのは、両方の入力に対するeの微分係数の両方、つまり $ \frac{\partial e}{\partial a} $ と $ \frac{\partial e}{\partial b} $ です。フォワードモード微分では「1つの入力に対する出力の微分係数」が得られるだけですが、リバースモード微分ではそれらの全てが得られるのです。

このグラフでは、計算速度は2倍にアップしただけですが、例えば100万の入力と1つの出力を持つ関数があると考えてみてください。フォワードモード微分だと、微分係数を得るのにグラフを100万回行き来しなければなりませんが、リバースモード微分だと1回の降下で全てが得られます。100万倍のスピードアップともなれば、その魅力も100万倍です。

ニューラルネットワークの学習においては、パラメータ（ネットワークの挙動を記述する数字）の関数としてコスト（ニューラルネットワークの不適切な実行を記述する値）を考えています。 最急降下法 を用いるには、全てのパラメータに対するコストの微分係数を計算する必要があります。また、ニューラルネットワークではパラメータが100万あるいは1,000万あることも珍しくありません。そんな時、リバースモード微分（ニューラルネットワークではバックプロパゲーションと呼ばれています）がスピードアップの大きな力となってくれるのです。

（逆にフォワードモード微分が理に適っているような状況はあるのでしょうか。もちろん、あります。リバースモードでは、全ての入力に対して1つの出力の微分係数が得られますが、フォワードモードでは、1つの入力に対して全ての出力の微分係数が得られます。つまり、出力の数が多い関数の場合、フォワードモードの方がはるかに高速に計算できるというわけです。）

これは些細なことか？

私が初めてバックプロパゲーションとは何か理解した時は、「ああ、これはまさに連鎖律だ！　考案されるまでなぜこんなに時間がかかったんだ？」と思いました。そう思ったのは私だけではありません。事実、「フィードフォワードニューラルネットワークの微分係数を計算するための良い方法はないだろうか？」と思案した場合、この考えに行きつくことはそう難しいことではありません。

しかしこれは見かけよりはずっと難しかったと私は思います。ご存知のように、バックプロパゲーションが考案された当時、フィードフォワードニューラルネットワークはそれほど注目されていませんでした。また、微分を学習に使うのが正しいのかも定かではなかったのです。微分を速く計算するには循環依存の関係を使えばよかったのですが、みんなが気づいたのはあとになってのことでした。

さらに悪いことに、「循環依存は使用できない」と見切りをつけるのはとても容易でした。ニューラルネットワークの学習に微分を使う？　間違いなく極小値で行き詰まるだけです。それに全ての微分係数をコンピュータで計算すると高くつくのは明らかでしょう。そのアプローチでうまく行きそうにない理由のリストアップをすぐ始めたりしないのは、うまく行くことを今なら知っているからに過ぎません。

これは後知恵というものです。質問をする時には、一番大変な仕事は終わっているのです。

まとめ

微分はあなたが思うより気軽に使えます。それがこの記事における主な教訓です。微分が手軽なのは論理的な事実なのですが、私たち愚かな人類はその事実を何度も再発見しなければなりませんでした。ディープラーニングを理解するのは大事なことです。そして、他の分野を知ることは、特にそれが周知の事実ではない場合、大変役に立ちます。

他にも教訓があるかって？　あると思いますよ。

バックプロパゲーションは、あるモデルで微分の流れを理解しようとする時にも大変便利です。流れがわかることは一部のモデルの最適化が困難な理由を説明するのにとても役立ちます。典型的な例としては、リカレントニューラルネットワークにおける勾配ベクトルの減少が挙げられます。

最後に私は、これらの技術からアルゴリズムに関する一般的な教訓を得られると断言します。バックプロパゲーションとフォワードモード微分は一組の強力な手段（線形化と動的計画法）を使って、人が想像する以上に効果的に微分を計算します。これらの技術をきちんと理解すれば、微分を含むいろいろな興味深い式を効率よく計算できます。私たちはこのことを今後のブログ記事で掘り下げていく予定です。

この記事ではバックプロパゲーションのごく概要的な処理にのみ触れました。Michael Nielsenが書いた記事の この章 を読むことを強くお勧めします。考察に優れ、ニューラルネットワークに関してより具体的に焦点が当てられています。

謝辞

この記事の校正をしてくれた Greg Corrado 、 Jon Shlens 、 Samy Bengio 、 Anelia Angelova に感謝します。

それから、バックプロパゲーションをどう説明するか議論してくれた Dario Amodei 、 Michael Nielsen 、 Yoshua Bengio にも感謝します。そして、討議やセミナーの席で、私がバックプロパゲーションの説明を練習することを許してくれた皆さん、ありがとうございました！

注釈