前回は、グラフィックカード上だけで コンウェイのライフゲームを実行するアイデアを説明しました 。このアイデアは、3つ以上の状態を有するオートマトンを含め、 どのような セルオートマトンにも当てはめることができます。今回の投稿では、二次元グリッドの 最短経路問題 をGPUだけで解決するのに、このアイデアを活用してみたいと思います。CPUによる従来の検索と比べても、その速さは遜色ありません。

JavaScript側の状態は基本的に以前と同様なので（2つのテクスチャと、それらを繋いでオートマトンを次のステップに進めるフラグメントシェーダ）、ここでは説明は割愛します。変更したのは次の2点、（オートマトンの全ての状態を表現する）セルの状態のエンコーディングと（新しいルールをプログラムする）フラグメントシェーダです。

• オンラインデモ （ ソース ）

デバッグや実験のために使ったセルオートマトンの純粋なJavaScriptの実装（State.js）が含まれていますが、実際のところデモでは使用されていません。フラグメントシェーダ（12state.frag）は、オートマトンの全ルールをGPU向けにエンコードしています。

迷路を解くセルオートマトン

任意次元のいかなる 完璧な 迷路をも解くことができる極めて単純な2状態のセルオートマトンがあります。各セルはOPEN（開放）かWALL（壁）のどちらかで、4近傍連結のみを考慮します。そして、ルールは1つだけ＝「OPENセルがOPENの近傍を1つしか持たない場合はWALLになる」です。

解決に向けて、行き止まりがステップごとにつぶれていきます。上のGIF画像で、スタート地点とゴール地点がつぶれないようにするため、私は3つ目の状態（赤）を追加してOPENの状態を維持するようにしました。GPU上では、最長の行き止まりの長さ分だけ描画を繰り返す必要があります。

ここで言う完璧な迷路とは、答えが1つしかない迷路です。抜け道やループ、オープンスペースなどが複数ある場合、上で紹介した手法は有効とはなりません。複数の解答があれば、つぶれた時に1つにはなりませんからね。もちろん、最短の経路でもなくなってしまいます。

これを修復するためには、さらに高度なセルオートマトンが必要です。

経路を見つけるセルオートマトン

迷路を解くだけではなく、具体的に最短の経路を見つける12状態のセルオートマトンを考えてみました。上と同じように、考慮するのは4近傍連結だけです。

• OPEN（白）：迷路内の通過可能スペース
• WALL（黒）：迷路内の通過不可能スペース
• BEGIN（赤）：スタート地点
• END（赤）：ゴール地点
• FLOW（緑）：4つの特徴（北：n、東：e、南：s、西：ｗ）を持つflood fill（塗りつぶし）
• ROUTE（青）：最短経路の解答、同様に4つの特徴を持つ

これを8近傍連結にしたい場合は、12の代わりに20状態（北：n、北東：ne、東：e、南東：se、南：s、南西：sw、西：ｗ、北西：nw）にしてやればいいだけです。あとは何も変える必要はありません。この経路探索のルールも至ってシンプルです。

• WALLとROUTEのセルは状態を変えない。
• OPENは隣接するセルがFLOWの時、FLOWに変わる。矢印は隣接したFLOWセルを指す（n、e、s、w）。
• ENDは隣接するセルがFLOWの時、ROUTEに変わる。矢印はFLOWセルを指す（n、e、s、w）。このルールは、複数の解答が現れないようにするためにも重要。
• FLOWは、隣接するROUTEセルの矢印がそれ自体を指している時、ROUTEに変わる。上記のルールとの組み合わせにより、FLOWセルがROUTEセルに触れるとカスケード反応となる。
• BEGINは隣接するセルがROUTEの時、ROUTEに変わる。この時、方向は重要ではない。このルール自体は必要不可欠というわけではないものの、後ほど重宝する。

これは、いかなる任意次元のセル状グリッドに対しても適用でき、高次元であってもGPU上で実行することが可能です。主として均一なテクスチャのバインド数に制限されます（2Dではテクスチャバインドが1回必要、3Dでは2回、4Dでは8回…のような感じでしょうか）。ただ、仮に5次元グリッドの最短経路を見つけたいという人がいるのであれば、ぜひお目にかかってその理由を伺いたいですね。

さて、それではどんな風になるかを見てみましょう。

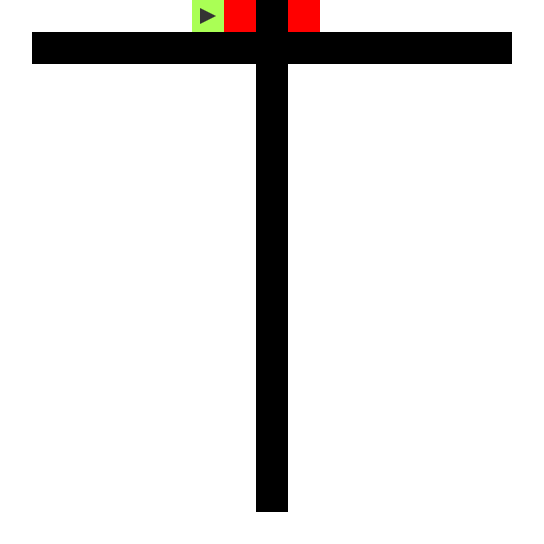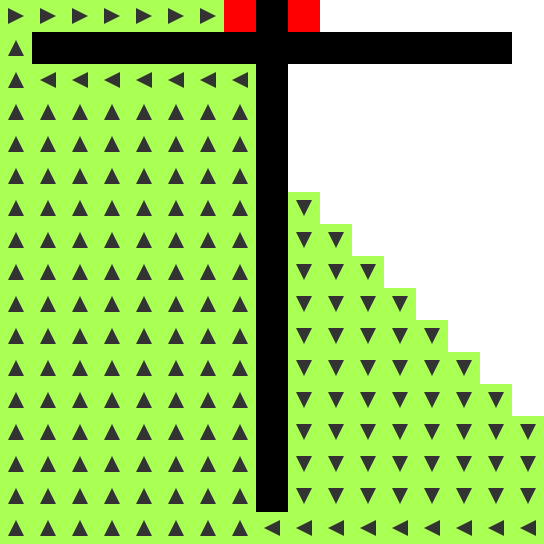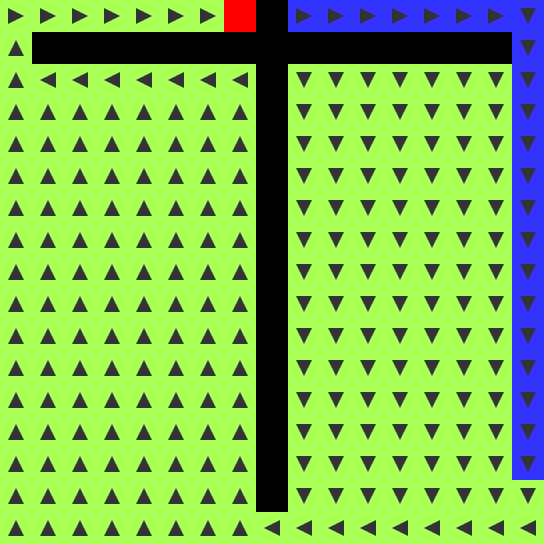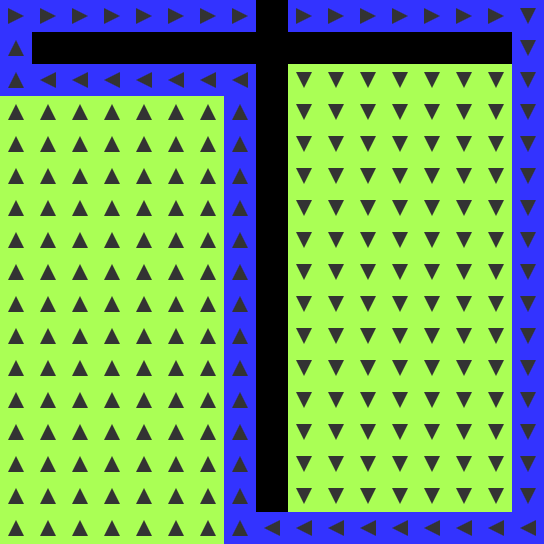
FLOWセルが迷路全体を塗りつぶす過程で、迷路の分かれ道が並列的に探索されつつ発見されていきます。ENDセルにたどり着いたら、FLOWのたどってきた経路に沿って、ROUTEがBEGINセルに向かってさかのぼります。ステップ数は、最短経路の長さ分の2倍が必要です。

なお、ENDにたどり着いた後でもFLOWセルによる迷路の塗りつぶしは続きます。これはセルオートマトンなので、解答が見つかったことを他のセルに知らせる方法はないのです。ただ、GPUで実行している場合、このことはさほど問題にはならないでしょう。全てのフラグメントシェーダが実行し終わらない限り、途中で終わることはありませんからね。

この経路探索の素晴らしい点は、迷路に限定されないことです。次の画像にはオープンスペースを持つ2つの部屋がありますが、ここでも経路は表示されます。

迷路の種類

解答のうち最悪なのは、最短経路が最長の距離になってしまうことです。境界が一辺しかないケースでオートマトン全部を実行して1つのセルを押し進めるのは、GPUにとっても非効率です。

セルオートマトンが答えを得る速さは、迷路が生成される方法に大きく影響されます。一般的な迷路生成アルゴリズムはランダムな深さ優先検索（DFS）です。迷路全体が完全に壁で囲まれた状態でスタートし、アルゴリズムはランダムに壁を倒しながら進みますが、その結果としてオープンスペースになることはありません。行き止まりに突き当ると、引き返して新たに倒すべき壁を探します。この方法では傾向として長くて曲がった経路になりがちで、枝分かれする要因は少なくなります。

デモでお見せしているのはクラスカルの迷路です。迷路内のどこでも、完璧な迷路のルールを破ることなく壁がランダムに倒されていきます。分岐因子がとても高いので、デモとしては面白くなります。

経路ステップをスキップする

私のコンピュータ上の1023×1023のクラスカルの迷路は、同じ迷路に対して A* （ rot.jsバージョン ） よりも約1桁遅く (下記のアップデートを参照してください)、 あまり感心できません。 この差は将来的には小さくなる はずです 。CPUの高速化と同様にGPUも高速化するからです。しかしここで重要なのは、GPUオートマトンによるアルゴリズムは、起点とゴール間の最短経路を解決するだけではなく、 起点と他のポイント間との最短経路を見つけられること です。本来これは 幅優先探索 ですからね。

アップデート ： この記事を書いた翌日、私は glReadPixels が非常に大きなボトルネックだということに気付きました。500イテレーション毎にend条件をチェックするだけで、この方法を最新のグラフィックカード上で行えばA*と同じくらい高速になりました。最大で499回無駄にイテレーションすることになるかもしれませんけどね。 あと数年もすれば、この手法はA＊よりも速くなるでしょう。

実際のところ、これはROUTEステップにおいてはあまり役立たず、GPUにとっては適合不良で、実際のアプリケーションにおいては全く役に立ちません。ここでは主にデモの目的のために使っています。探索に失敗した場合、セルオートマトンは6状態に遷移します。すなわちOPEN、WALL、そして4種のFLOWです。起点をFLOWセル（任意方向)でシードして、全てのOPENセルがなくなるまでオートマトンを実行します。

EndStateを検知する

ROUTEセルにも、もちろん有益な目的があります。終了したことを知るにはどうすればいいのでしょう？　BEGINセルを調べていつROUTE セルになったかチェックすればいいのです。そうすれば解が出たことが分かります。しかし、特にDFS迷路の場合は、これによって全てのFLOWセルが塗りつぶしを終了したことを意味するわけではありません。

CPUベースの解決策では、私はOPENセルの状態が変わる度にカウンタをインクリメントします。イテレーションの後にカウンタに変更がなければ終了です。OpenGL4.2では アトミックカウンタ が導入され、この役割を果たしてくれますが、OpenGL ES/WebGLではまだ搭載されていません。最後にすることは glReadPixels を使って全てを引き出して、CPUのend状態をチェックすることです。

上記、オリジナルの2状態のオートマトンもこの問題に影響を受けます。

セルの状態をエンコードする

セルはGPUテクスチャの中にピクセル毎に保存されています。セルの12状態をvc4 colorにエンコードするいい方法がないか考えるのに随分時間を使いました。たぶんセルの状態を更新する blendを使ったり 、他の種類のビルトインピクセル計算を利用したりする方法があるはずですが、私は単刀直入に0から11までを、単色のチャネル（私の場合は赤）へとエンコードする以上にいい方法は思いつきませんでした。

int state(vec2 offset) {
    vec2 coord = (gl_FragCoord.xy + offset) / scale;
    vec4 color = texture2D(maze, coord);
    return int(color.r * 11.0 + 0.5);
}

これで、他の有用な情報のため、まだ手のつけられていない3つのチャネルが残ります。私は緑色のチャネルで距離を書くのを試してみました（コミットしていません）。OPENセルがFLOWセルになる時、隣接するFLOWセルの距離に1を付加します。これは実際のアプリケーションではかなり便利なのではないでしょうか。GPUにマップを配置し、十分な回数セルオートマトンを実行し、マップを（ glReadPixels ）から引き離せば、全てのポイントで経路と起点からの総距離が分かります。

パフォーマンス

上述のように、私はGPUの迷路ソルバを実行してA*に競わせ、パフォーマンスをテストしました。ただ、まだグリッド全体で（起点は1つ、ゴールは多数）、CPU上でダイクストラ法と競わせたことはありません。推測するとすれば、GPUは高い分岐因子（オープンスペースなど）のグリッドに対してトップに来るので、その並行処理は最も効果的に生かされるでしょうが、その他の場合ではダイクストラ法が勝つでしょう。
これはアイデアの証明であって、実用的な用途のものではありません。OpenGLをいじって迷路を解けるという証明なのです。