(注：2017/02/06、いただいたフィードバックを元に翻訳を修正いたしました。修正内容については、 こちら を参照ください。)

Dependency HellはNP完全ですが、この状況から脱却できるかもしれません。

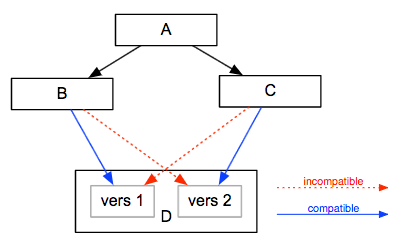
パッケージにおけるバージョン選択の問題とは、完全である（全ての依存関係を満たしている）かつ互換性のある（互換性のない2つのパッケージが選択されていない）トップレベルパッケージPをビルドするために使われる依存関係の集合を見つけることです。ただし、菱形依存問題があるので、このようなセットは存在しない可能性があります。菱形依存問題とは、AはBとCが必要、BはDのバージョン2ではなくバージョン1が必要、CはDのバージョン1ではなくバージョン2が必要といったような問題のことです。この場合、Dの両方のバージョンを選択することはできないため、Aをビルドすることができないわけです。

パッケージのバージョンを選択するために、パッケージ管理システムにはアルゴリズムが必要となります。つまり、 apt-get install perl を実行する際、システムがPerlの最新バージョンのことを指していると決めてかかるかもしれません。しかしこの場合、Perlの推移的依存関係を満たす方法を見つけるか、なぜPerlがインストールできないのか納得のいく説明を出力しなければなりません。この問題を解決するのに、最悪どのくらいのコストがかかるのかと、疑問に思うことでしょう。Perlをインストールすることができるかどうか判断するのに、パッケージ管理システムが何時間または何日、もしくは何年という時間を費やしてほしくないはずです。

残念ながら、バージョンを選択する問題はNP完全で、全ての入力に対して素早い実行が保証されたアルゴリズムを見つけられる見込みは非常に低いのです。この記事では、バージョン選択におけるNP完全性の検証を紹介するとともに、既存のパッケージ管理システムがどのように対処しているのかを見ていきながら、NP完全なタスクを避けるための有用なアプローチ方法を簡単にお話ししていきたいと思います。

NP完全性の検証

NP完全性を検証するためには、多様な出力のあるアルゴリズムの現代的な世界から、yesもしくはnoのどちらかを取るブーリアン出力を持つアルゴリズムである、複雑性理論の限定的な世界へと移行する必要があります。複雑性理論の世界では、VERSION問題（VERSIONは常に大文字）を定義し、有効なバージョン選択があるかどうかを要求します。ブーリアンのVERSION問題は私たちが持つ元々の問題の半分でしかなく、これがNP完全であることは証明可能です。この証明を行うには、VERSIONがNPに属していることと、そのVERSIONがNP困難であることの2つの異なる事実を証明する必要があります。

解 “yes” の全てに、検証が容易な多項式サイズの説明が含まれている場合、ある問題はNPに属することになります。

選択されたパッケージのバージョンをリストすることによって、解 “yes” のどれも説明することができるので、VERSIONはNPに属することになります。このリストは入力よりも大きくなることはなく、時間内に正確性を確認することができ、入力の二乗よりも悪くなることはありません（計算モデルの詳細によっては、線形かもしれません）。

ある問題に対する有効な解決策が、NPに属する他の全ての問題に対する有効な解決策に適合できる場合、問題はNP困難となります。これは非常に難しい注文ではありますが、VERSIONに対する有効な解決策を、もう1つのNP困難の問題（HARDと呼びます）に対する有効な解決策に適合させることを証明するだけで十分です。そして、他の誰かが証明したHARDに対する有効な解決策が、NPに属する他の全ての問題に対する有効な解決策に適合できるという事実に依存すればいいのです。

NP完全（NPとNP困難）の有用な例に、充足可能性問題があります。充足可能性問題では、入力は、変数もしくはその変数の否定である、3つそれぞれのリテラルを論理和（OR）で結び、それらを論理積（AND）で結ぶように制限されたブーリアン変数のブーリアン方程式となります。充足可能性問題の入力として以下の例を挙げておきます（∧はAND、∨はOR、¬はNOT）。

(¬ x1 ∨ ¬ x2 ∨ ¬ x3) ∧ (¬ x2 ∨ ¬ x3 ∨ ¬ x4) ∧ (¬ x2 ∨ ¬ x2 ∨ x3) ∧ (x2 ∨ x2 ∨ x2)

x1 = 0、x2 = 1、x3 = 1、x4 = 0のように、変数にこのような組み合わせの数値を代入することによって充足可能になります。よって解はyesです。

以下のように、節をもう1つ追加した場合はどうでしょうか。

(¬ x1 ∨ ¬ x2 ∨ ¬ x3) ∧ (¬ x2 ∨ ¬ x3 ∨ ¬ x4) ∧ (¬ x2 ∨ ¬ x2 ∨ x3) ∧ (x2 ∨ x2 ∨ x2) ∧ (x1 ∨ ¬ x2 ∨ x4)

この場合、変数にどのような値を代入しても充足不可能なので、解はnoです。

充足可能性問題のインスタンスの一般的な形式は、変数V1からVmに対する節C1からCnの論理積から成る方程式Fです。ここで各Ciは3つのリテラルの論理和で、それぞれのリテラルは変数xjを用いてxjまたは¬ xjの形式をとります。項にある重複したリテラルは、上記にある(¬ x2 ∨ ¬ x2 ∨ x3)や(x2 ∨ x2 ∨ x2)のようにすることができます。

どのような充足可能性問題のインスタンスでも、同じ解となるVERSIONのインスタンスに置き換えることができます。パッケージ管理については、以下についてのみ仮定することとします。

1.パッケージは0個以上のパッケージのバージョンまたは特定のパッケージのバージョンを依存関係としてリストすることができる。
2. パッケージをインストールするには、依存関係のあるこれら全てのパッケージがインストールされなければならない。
3. パッケージの各バージョンは、異なる依存関係を持つことができる。
4. 2種類の異なるバージョンのパッケージを同時にインストールすることはできない。

バージョンVのパッケージPをP:V（方程式の標準数式イタリックと区別するためにパッケージについては等幅フォントを使用しています）という形に省略します。P:Vの依存関係は、V-1やV+1ではなく、バージョンVによって完全に満たされなくてはなりません。

充足可能性問題の方程式が与えられれば、パッケージFを作成することができます。このFは方程式全体、パケージC1, C2, …, Cnはそれぞれ項を、パッケージX1, X2, …, Xmは各変数を表しています。

各パッケージX j はX j :0とX j :1という2つのバージョンを持っています。上記のことを仮定した場合、X j :0とX j :1は競合関係にあり、両方をインストールすることはできません。元々の方程式では、インストールされているX j :1がx j =1に対応しています。

パッケージC i は数字0、1、2という3つのバージョンを持っていて、それぞれのバージョンは対応する項のリテラルによって決まります。例えば、 C ₅ が( x ₁ ∨ ¬ x ₂ ∨ x ₄ )である場合、C5:0がX1:1に、C5:1がX2:0に、C5:2がX4:1によって決まります。元々の方程式では、インストールされているC i:k は、真である C (i) の k 番目のリテラルに対応します（結果、 C (i) が真となります）。

パッケージFは、C1、C2、…、C n によって決まります。インストールされているFは、全てのC (i) がインストールされることを示しており、これによって真となる全ての C (i) に対応することになるので、結果、 F が真となります。

パッケージ管理がパッケージFをインストールする方法を見つけることができれば、元々の方程式を満たす代入は、各変数x jに対するX j:1のインストール状態から読み出すことができます。同様に、方程式が充足可能なのであれば、満足できる代入は、パッケージ管理がFのインストールを問題なく実行する1つの方法を与えてくれるでしょう。それ故に私たちは、同じ解法を用いることで、充足可能性問題のインスタンスを、対応するVERSIONのインスタンスに置き換えました。これにより、充足可能性問題はVERSIONを使うことで解決できると定めることができ、VERSIONはNP困難ということになります。

VERSIONがNPに属していてNP困難であることから、VERSIONはNP完全となります。

実装

上記はかなり最低限の場合を仮定しています。パッケージは依存関係のリストを持っていて、パッケージの依存関係は独自のバージョンからバージョンに変更することが可能。パッケージの依存関係は特定の依存関係のバージョンを制限可能。2つのパッケージのバージョンはお互いに競合しうる。これはパッケージ管理システムを役立たせるには最低限必要なことでしょう。いくつかのパッケージ管理では、依存関係が特定のバージョンをリストすることを許可しない代わりに、範囲を必要とします。しかし、バージョンの必要条件0と1は≤ 0と≥ 1へと簡単に変更することができます。いくつかのパッケージ管理は、初期設定でパッケージの異なるバージョンの競合を想定できないかもしれませんが、最低でも次に挙げるようなことは特定することは可能かもしれません。Unixシステムに2つの /bin/bash が存在することはない、または、 printf という2つの定義がCプログラムに組み込まれている。

仮定は、調べた全てのパッケージ管理システムに当てはまります。調べたシステムは、DebianのAPT、RedHatのRPM、RustのCargo、Nodeのnpmjs、JavaのMaven、HaskellのCabal、等々です。つまりこれらのパッケージ管理システムは、NP完全なタスクに直面していることを意味します。インストール方法を決めるために長い時間を要する可能性があるのか、それともインストールできないものとしてインストール可能なパッケージを報告する可能性があるのか、それぞれのパッケージ管理システムは選択しなければなりません（もちろん、何らかの事情により、所与の実装が両方を行うこともあります）。
Knuthは The Art of Computer Programming Volume 4, Fascicle 6 で以下のように記述しています。

充足可能性の話は、美しい数学を織り交ぜたソフトウェアエンジニアリングの勝利を語るものです。見事な新しいデータ構造やその他のテクニックのおかげです。このような問題は、数年前までは対処するのが不可能と考えられていましたが、現代のSATソルバでは多くの変数が絡んだ現実の問題に当たり前のように対処できるようになっています。

実際のところ、現代のパッケージ管理はSATソルバの使用へと移行し始めています。

0install はヒューリスティックから開始しましたが、 SATソルバ に移行することが 必要だと分かりました 。

システム統合フレームワークである Chef は、 Gecodeの制約ソルバ として Rubyバインディングのdep-selectgor を使っています。

Dartのpub には、 しばしば長い時間を要する バックトラッキングソルバ が含まれています。

Debianのapt-get は、初期設定でヒューリスティックを使っていますが、 SATソルバを呼び出す ことができ、 ユーザプリファレンスを考慮する こともできます。また、Debianの品質保証チームも、リポジトリ内でインストールできないパッケージを特定するために ソルバを実行しています 。

Eclipse は、 プラグインのインストール状況を管理する ために、 sat4j SATソルバ を使っています。

FedoraのDNF （または “Dandified yum” ）では、実験モードで SATソルバ を使っています。

FreeBSDのpkg （DragonflyBSDでも使われています）では、 picosat SATソルバ を使っています。

OCamlのOPAM は、 ローカルまたはネットワークを介してリモートでSATソルバを呼び出す ことができます。Debianのapt-getのように、OPAMのソルバはユーザプリファレンスを考慮することができ、OPAMのリポジトリはインストールできないパッケージに対してスキャンが実行されます。

Open SUSE のパッケージ管理は、 “充足可能性のアルゴリズムを使っているフリーパッケージの依存関係ソルバ” である libsolv を使っています。また、独自の libzypp SATソルバを使うOpenSUSEのzypperもあります。

PythonのAnaconda は、 SATソルバ を使っていますが、 長い時間を要します 。

RustのCargo では、 基本的なバックトラッキングソルバ を使っています。これにより複数のバージョンが最終的なバイナリにリンクされます。

Illumosでも使用され、またIPSとしても知られる Solarisのpkg は、 minisat SATソルバを使っています 。

Swiftのパッケージ管理 では、 基本的なバックトラッキングソルバ を使っています。

（こちらに他のパッケージ管理を追加したいと思っているので、詳細をご存じの方（または記載されている内容に間違いがある場合）は 私宛にメールしていただくか 、 ツイートを送ってください 。よろしくお願いします）

代替案？

パッケージのバージョン選択がNP完全であるという事実に、私たちはどう反応すべきでしょうか？　1つの反応としては、複雑性を受け入れ、SATソルバが優れていることに感謝することでしょう。別の反応としては、これが良い方法なかどうかを問いかけてみることです。この問題を解決することを要求するようなツールをビルドすべきではないかもしれませんし、またソフトウェアを開発する過程で何か不具合が起こる可能性もあります。

パッケージのバージョン選択がNP完全問題なのであれば、それはつまり、考えられるパッケージの組み合わせの探索空間が大きく、効率の良い体系的分析が複雑だということです。効率の良い体系的テストはどうでしょうか？　もし探索で競合しない組み合わせを見つけたとして、その組み合わせが機能するとなぜ信じることができるのでしょうか？　バージョンの競合がないということは、組み合わせがテストされていないということだけを意味します。探索が競合しない組み合わせを見つけられなかった場合、次のステップを明確にするために、開発者にその失敗をどのように説明することができるでしょう？ ソフトウェアのコンフィギュレーションの決定にNP完全な問題を介入させずにソフトウェアをきちんと理解するのは非常に難しいものです。それでは、ここまでのおさらいと、どのように回避できるかを検証していきましょう。

上に示した証明は、前述の仮定に左右されます。その仮定をもう一度、以下に示しておきます。

1. パッケージは0個以上のパッケージまたは特定のパッケージのバージョンを依存関係として列挙できる。
2. パッケージをインストールするには、依存関係のあるこれら全てのパッケージがインストールされなければならない。
3. パッケージの各バージョンは異なる依存関係を持つことができる。
4. 2種類の異なるバージョンのパッケージを同時にインストールすることはできない。

先に私が提示したように、これらは “パッケージ管理を役立つものとするための必要最低限” に相当する、と一般に通用しています。しかし、最終的にはこの仮定を削減する方法を見つけることができるかもしれません。

NP完全性を回避するための1つの方法は、仮定1に取り組むことです。もし仮に、依存関係に、特定のパッケージのバージョンをリストするのではなく、最小バージョンしか明記できないとしたらどうなるでしょう？ この場合は、使用するパッケージを見つけるために、次のようなちょっとしたアルゴリズムがあります。インストールしたいものの最新バージョンから始めて、その全ての依存関係の最新バージョンを、再帰的に入手します。この記事の冒頭、最初の菱形依存問題で、AはBとCを必要とし、BとCは異なるバージョンのDを必要とします。BはD 1.5を必要とし、CはD 1.6が必要とするなら、ビルドは両方に対しD 1.6を使うことができます。もし、BがD 1.6で動作しないなら、BのバージョンあるいはD 1.6のどちらかにバグがあると考えられます。バグのあるバージョンは配布から完全に削除しなければなりません。またその後、新しくリリースしたバージョンで問題を修正する必要があります。逆に依存関係グラフに競合を加えることは、問題を修正せずにバグを付加しているようなものです。

NP完全性を回避する別の方法は、仮定4に取り組むことです。もし仮に、2つの異なるバージョンのパッケージを同時にインストールすることができるとしたらどうなるでしょう。ほとんど全ての探索アルゴリズムは、プログラムをビルドするためのパッケージの組み合わせを探すでしょう。それは、もしかすると最小限の組み合わせではないかもしれません（それはまだNP完全です）。BがD 1.5を必要とし、CがD 2.2を必要とするなら、ビルドは、両方を最終的なバイナリに含めて、個別のパッケージとして扱うことができます。上述のように、2種類の printf の定義をCプログラムに組み込むことはあり得ませんが、明示的モジュールシステムを有する言語は、（完全修飾名が異なるという保証の下）Dの個別のバージョンをプログラムに含めることに、何の問題もありません。

NP完全性を回避する別の方法は、上で述べた2つを組み合わせることです。すでに示した例のように、もしパッケージが セマンティック バージョニング に従えば、パッケージ管理は自動的にメジャーバージョンの中から最新バージョンの依存関係を使うでしょう。しかしその一方で、異なるメジャーバージョンを別のパッケージとして扱います。

このような制限の根本原理の1つは、開発者がソフトウェアをビルドしたりテストしたりする際に、考えられる全てのパッケージの組み合わせ全体について考えきれていない可能性があるということです。この考え方は、ソフトウェアのビルド方法について開発者とツールが整合性を保つ際に役立ちます。これらのアプローチのいずれかを実際に実行させることができれば、言語のパッケージ管理の操作性と理解性を大いに簡素化できるでしょう。

関連著書

DebianとRedHatのパッケージのインストレーションがNP完全であるという証明は、 EDOS dekuveravke WP2-D2.1、ソフトウェア依存関係の形式的管理に関する報告書 （2005年）の49～50ページに掲載されています。インストレーションをパッケージ化するための充足可能性問題の削減における、困難な手順は論理和をどのように構成するかということです。EDOSの証明は、単一の依存関係に対する代替リストを特定するパッケージ管理の機能を使って、直接に（Debianの場合）、あるいは “provides” ディレクティブ（RedHatの場合）を用いて、論理和をエンコードします。例えばこれらのシステムでは、実際のパッケージである ed や vi 、 acme のいずれかがインストールされていれば、擬似パッケージである text-editor がインストールされていると考えるのは明らかです。

RustのCargoのような言語のパッケージ管理の、依存関係の仕様書はDebianやRedHatの仕様書よりもはるかに簡素なものです。ですから、EDOSの証明は当てはまりません。そのため、言語のパッケージ管理はより簡単な（NP完全ではない）ジョブに直面することが望まれるかもしれません。上述の新しい証明はその望みをはねのけてくれるでしょう。（この証明を確認するための1つの方法は、 ed 、 vi 、 acme のそれぞれに由来する3つのバージョンの text-editor パッケージを定義して、最後の例で述べた “provides” 命令をシミュレートすることです。）

パッケージの異なるバージョンの依存関係を変更して論理和をエンコーディングすれば、DebianやRedHatのパッケージ管理の両方に対して、修正することなく新しい証明が機能するだけでなく、いかなる予見可能なオペレーティングシステムや言語パッケージ管理に本質的に適用できるのです。言語のパッケージ管理の作成者のほとんどは、自分たちが直面した問題をNP完全とみなしていたと想像していますが、その事実が事前に証明されていたとする書面を見つけることはできていません。

依存関係を持つ、いくつかのシステムではSATソルバの代わりに制約ソルバを使っています。しかし、根本的な問題は、 なおもNP完全であるということ です。

2008年、Daniel Burrowsは dpkgを用いた数独問題の解法 に関する記事をブログに投稿しました。

EDOS報告書を私に示唆してくれたSam Boyerと、彼の優れた パッケージマネージメントの概要 に感謝します。

Roberto Di Cosmoは、EDOS報告書に続くものをたくさん書いています。 こちらがそのリストです 。特に、「 依存関係の解法、コンポーネントの進化するマネジメントでの個別の懸念 」には、最新版の証明が含まれています。その一連の研究はSATソルバに適用するだけでなく、ユーザプリファレンスを考慮に入れて動作します。

また別の関連著書には、2007年ICSEで発表されたTuckerらの
「 OPIUM、最適なパッケージのインストール／アンインストール管理 」、があります。OPIUMは 0installソルバの出発点 です。

Jaroslav Tulachは 2009年に、上で述べたのと同じ証明 を発見しました。ハンドル名 edwintorokという読者のリンク に感謝します。

Webサイト、 LtUでのTulachの証明に関する議論 では、2005年のDaniel Burrowsの論文「 ソフトウェア依存関係のモデリングとリゾルビング 」に触れていますが、この論文の証明は、Tulachの証明／上述の証明よりもEDOSの証明に近いでしょう。

多くの読者が、参考文献や、SATソルバを有するパッケージ管理の追加のリンクを送ってくれました。みなさんどうもありがとうございます。