2015年11月12日
マジックカーネル – 画像のリサンプリングのメソッド

本記事は、原著者の許諾のもとに翻訳・掲載しております。
マジックカーネルとは?
“マジックカーネル”とは、極めて高速で(一番単純なバージョンなら、必要なのは少しの整数加算とビットシフトのみです)、驚くほどの結果を出してくれる効果的な画像のリサンプリングのメソッドです(エイリアシングノイズやリンギング、細かい物体の”Width beat”の発生を防ぎます)。
私がこのマジックカーネルと出会ったのは2006年、一般的に使われているJPEGライブラリのソースコードを扱っていた時のことです。それ以来、この素晴らしい特性を深く探り、任意のリサンプリングファクタのケースにまでこのメソッドを広げました。
このWebページでは、それらの特性を要約して説明し、画像への適用も含めてマジックカーネルのC#のコード実装の全てをご紹介します。
マジックカーネルはどこから来たのか
2006年に私は、JPEGを過剰に圧縮すると発生するブロックノイズを最小限に抑えるいい方法はないか探っていました(詳細は こちら をご覧ください)。その結果、私は一般的によく使われている、Cで記述され、Independent JPEG Group (IJG)によって作成されたJPEGライブラリを活用しました。スタンダードなJPEG圧縮は、2チャンネルのクロミナンスデータを半分の解像度で保存します。例えば、2×2ピクセルのブロックに、CrとCbそれぞれ1つの値のみを保存する、というものです。すなわち、画像を再構築する時、解像度を戻すためにクロミナンスチャンネルを”アップサンプリング”する必要があります。
一番簡単なアップサンプリングのメソッドは、単純に2×2ピクセル全てにそのブロックの値を複製する方法です。しかし、IJGライブラリにはクロミナンスの”ファンシーアップサンプリング”というオプションもあります。次の画像(オリジナルの倍のサイズ)を見ると、再構築後の結果の違いがよく分かります(特に、赤と黒の境目に注目してみてください)。

“複製”によるアップサンプリング

“ファンシー”アップサンリング
ということで、私はこの”ファンシー”アップサンプリングのCのソースコードを調査しました。驚くことに、これは各方向に{1/4, 3/4, 3/4, 1/4}という値を持つただのカーネルでした(スタンダードな”複製”カーネルは{0, 1, 1, 0})。
私はこのカーネルを、画像のサイズを倍にすると各方向で影響があるような一般的な画像に試そうと決めました。そしてまたもや驚くことに、何回もアップサンプリングを繰り返しても、いい状態を保てたのです。私はこれを”マジックカーネル”と名付けました。さらに驚いたのは、その結果が、PhotoshopやGIMPで一般的に使われているバイキュービック法のリサンプリングよりも視覚的に段違いに優れていたのです(さらにGIMPのLanczos-3 アップサンプリングよりも優れていました。しかし、Lanczos-3のGIMP実装は壊れていると後に知りましたので、比較の対象からは一時的に外しています)。

オリジナル画像

マジックカーネル1回

マジックカーネル2回

マジックカーネル3回

バイキュービック法:アーティファクトがあります
さらに、ダウンサンプリングカーネルを適用すると以下のような驚くほど美しい画像になります

新しいオリジナル画像

マジックカーネル1回

マジックカーネル2回

マジックカーネル3回
驚愕しました。このカーネルはどの教本やWebを見ても載っていません。私はいくつかのニュースグループにこれが有名かと尋ねました( こちら と こちら をご覧ください。)答えはノーでした。
なぜマジックカーネルは優秀なのか
私は大学で電気工学を勉強していた時、フーリエの定理の応用を学んでいました。そして、その定理を仮想粒子物理学で最も複雑な公式の中のいくつかに適用しました( こちら をご覧ください)。私は”正しい”アンチエリアシングカーネルはsinc関数であるということは知っていました。実際のところ、sinc関数は、無限の範囲の入力を用いるうえに負の値も取るため、近似が必要です(Lanczosカーネルのような)。
ここで生じる疑問は、一体なぜ単純なカーネル{1/4, 3/4, 3/4, 1/4}が”正しい”カーネルなのか、ということです。
この答えには2つあります。
1つ目は、上記で触れたニュースグループでの議論で見たように、新しくサンプリングした位置がオリジナルの位置からオフセットされるとしても、このカーネルがsinc関数をとてもシンプルに近似しているからです(オリジナルのJPEGクロミナンス実装の”タイル化”を考えるとこれは明らかですが、サンプリング定理という観点からは考えるとそうではありません)。Charles Bloom氏が 最近言っているのは 、このカーネルは、「ニアレストネイバー法によるアップサンプリングと、正規化された{1/4, 1/2, 1/4}カーネルのたたみ込み」として分解できるということです。
2つ目は、このカーネルを任意の回数繰り返し適用すると、ユニークで非常に望ましい性質を持つ一連のカーネルを導き出すということです。これが次の項目のテーマです。
連続のマジックカーネル
なぜマジックカーネルが画像に繰り返し適用した時に驚異的にうまく機能してくれるのか調査した結果、任意の回数たたみ込みをする時に、結果としてあらわれるカーネルは常に”3次放物線”で、これによりカーネルは一定のソース信号をたたみ込みする際に”適合”することがわかりました。
これを論理的な結論に応用すると、信号をマジックカーネルで無限回アップサンプリングする時に何が起こっているのかが見えてきます。 オリジナル のサンプリングされた空間(オリジナルの信号はxが整数値の箇所でサンプリングされるものとします)の座標をxとすると、無限にアップサンプリングをできる 連続のマジックカーネル は以下のように解析的に表せます。

この関数をグラフで示すと以下のようになります。
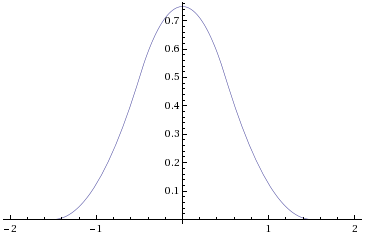
これではsinc関数には全く見えません。では、うまく機能する方法や理由は何でしょう。
1つ目は、m(x)は有限の範囲の信号の値しか用いないことです。つまり、オリジナルの信号の与えられたサンプルは、左右で1.5の位置の範囲にしか影響を与えません。これは実際に使う際には非常にいいことです。一方、sinc関数は無限の範囲の値を用います。常に制限のある実際の信号処理に用いることについて、その理論的妥当性に関して重要な疑問が生じます(この”境界条件”問題の詳細は、前述した物理学の文書で確認できます)。
2つ目は、m(x)は負の値をとらないということです。繰り返しになりますが、これにより多くの入力に対して負の値をとるsinc関数を使った際に生じる実用上の問題を避けることができます。そして、これはsinc関数の理論的”正しさ”を無効にする実用的近似法につながります。
3つ目は、m(x)は連続的で、その一次導関数も常に連続であるということです。マジックカーネルによる畳み込みが”良い結果に見える”のはこのおかげです。カーネルやその一次導関数の不連続性は、通常は人間の目でも確認できるようなアーティファクトを発生させるからです。これらの数学的な性質はsinc関数についても同様ですが、実用的近似法では必要ありません。
4つ目は、m(x)の形は、ガウス関数の形に視覚的に似ているということです。(もしフーリエの定理について何も知らない人であれば)ガウス関数を補間カーネルに選ぶのは数学者にとって自然なことでしょう。m(x)の標準偏差は上記の関数形式から求めることができ、その答えは1/2です。m(x)と、同じ標準偏差のガウス関数を比べると、近似は幻想でないことが分かります。
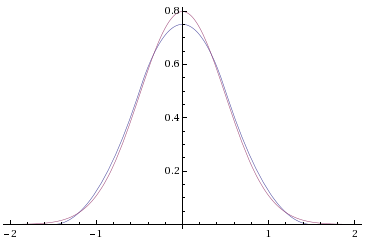
驚くことに、1980年代初期のピラミッドエンコーディングに関する独創性に富んだ研究で、{0.05, 0.25, 0.4, 0.25, 0.05}という5つの係数からなるフィルタのガウシアンと全く同じような性質を発見したのです( こちら と こちら をご覧ください)。
対照的に、sinc関数は周期的な値を取るため、スムーズな補間関数として直感的に選び難いものがありますし、実用上には強制的な打ち切りが必要です。
ガウス関数とは違って、m(x)は有限範囲の値を用いればよいので、隣接した3つの信号値のみが必要なります。ガウス関数を実用する際には、有限範囲に抑えるために打ち切りが必要ですが、それがアーティファクトを生成するということがここからわかると思います。
しかし、m(x)の一番重要な性質は、まず実質的に不利益な特徴のように見えるものに由来します。それは、「x = 0における値が3/4しかない」ということです。一方でsinc関数ではx = 0の時は1で、xが他の整数の時には0になります。数学的にはこれは 射影演算子 ということになり、任意の回数適用しても質を全く落とさないことになります。では、そうではないm(x)がいい仕事をしてくれるのはなぜでしょう。
実際に以下のような疑問が私の頭に浮かびました。なぜ単純に、サポート範囲が-1~+1の間である別の3次放物線のリサンプリングカーネルとしないのでしょうか。そうすれば、x = 0の時は1で、いとも簡単に隣接したコピーに適合します。具体的には以下のような形です。
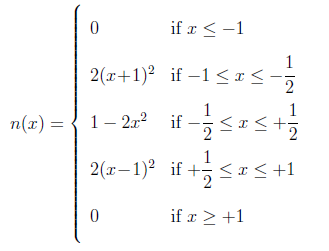
このようなカーネルの問題は、以下のような思考実験を行った時に見えてきます。信号を 同じ 間隔の格子点でリサンプリングしたいけど、非整数のfによって位置をオフセットするとどうなるでしょう。
x = 0の時に値が1であり、xが他の整数の場合は全て0である信号を入力した場合を思い浮かべてください。f = 0であれば、n(x)でたたみ込む時は、信号は変化しませんが、m(x) でたたみ込む時には値は{1/8, 3/4, 1/8}まで広がります。これを、vの空間変化があるような表示装置で利用するためにピクセルレスポンス関数でたたみ込むと、リサンプリングされた信号の全体の空間変化は、m(x)ではv + 1/4ですが、n(x)ではvのみになります。
こうして見るとm(x)よりn(x)のほうが優れているように見えませんか?
いいえ、それは違います。f = 1/2の場合を考えてみてください。m(x)もしくはn(x)のどちらでたたみ込みをしても結果は同じ{1/2, 1/2}となります。ピクセルレスポンス関数でたたみ込むと、m(x)でもn(x)でもv + 1/4の空間変化という結果になります。
では次は、オリジナル空間とは少し違う空間をリサンプリングする場合を考えてみましょう。カーネルn(x)はオリジナル空間で”ビート”します。つまり、リサンプリングされた信号の変化がvとv + 1/4の間で動くような干渉模様を作り出すのです(例えば、画像全体を横切るような細い線が太くなったり細くなったりすること)。対照的に、m(x)でたたみ込むと、 fがどんな値でも v + 1/4の定数分散が導き出されます。
ということで、マジックカーネルがx=0で3/4だけの値を取ることが、無害というだけではなく、リサンプリングカーネルとしての忠実性にとって重要である理由がわかりました。それは、リサンプリングの頻度や位相のオフセットには関係なく、画像の中で干渉模様が出ないことを保証してくれるのです。
マジックカーネルは、本当に素晴らしいんです!
ソースコード
マジックカーネルをC#コード実装 (14.6 KiB, zipped)
株式会社リクルート プロダクト統括本部 プロダクト開発統括室 グループマネジャー 株式会社ニジボックス デベロップメント室 室長 Node.js 日本ユーザーグループ代表
- X: @yosuke_furukawa
- Github: yosuke-furukawa