この数年で、プログラミング言語（PL）や機械学習のコミュニティは 確率的プログラミング（PP） を用いて、それぞれに共通する研究の関心事を明らかにしてきました。その概念は、抽象化のような強力なPLのコンセプトを”エクスポート”し、現状では複雑で困難な作業である統計的モデリングに再利用することができるかもしれない、というところにあります。

（講義ノートの 最新版 を閲覧したい方は、リンクをクリックしてください。ソースは GitHub に投稿してあります。誤りを発見した場合は、Pull Requestを送信してください。）

1. 何、そしてなぜ

1.1. 確率的プログラミングは○○○ではない

直観に反して、確率的プログラミングとは確率的に振る舞うソフトウェアを書くことでは ありません。 例えば、暗号のキー・ジェネレータやOSカーネルでの ASLR の実装、または回路設計のための 焼きなまし法 の最適化といったように、これから行おうとしていることの一部として、プログラムが rand(3) を呼び出す場合などはそういった理解で結構ですが、それらは確率的プログラミングが取り扱う内容とは違います。

“ソフトウェアを書く”とは全く考えないことがポイントです。例え話をすると、C++やHaskell、Pythonといった従来の言語は明らかに設計思想が異なる言語ですが、これらの言語を使ってあなたの猫の写真をアルバムにしたりLaTeXに代わる素晴らしい文書処理システムを書くことは（やれと言われれば）想像できますよね。ある領域について、この言語の方が他よりも優れているということはあるかもしれませんが、どの言語でも作ることはできるわけです。確率的プログラミング言語（PPL）の場合は、そうではありません。どちらかと言うと、Prologに似たようなものです。確かにプログラミング言語ではあるのですが—本格的なソフトウェアを書くのに適したツールではありません。

1.2. 確率的プログラミングとは

一方、確率的プログラミングは 統計的モデリングに適したツール です。プログラミング言語の世界から知恵を拝借し、統計的モデリングを設計・使用する際の問題にそれらの知恵を適用します。専門家は、論文上に数学的に表現された統計的モデルをすでに手作業で構築していますが、これは専門家だけが処理することができるプロセスで、機械的な推論で証明することは難しいものです。PPにおいて重要なインサイトは、統計的モデリングはそれを十分に行えば、多くの点でプログラミングのように感じ始めるということです。もしPPが躍進してモデリングに実世界の言語を使うことができるようになると、多くの新しいツールが実現できることになるでしょう。それぞれの事例ごとに論文を書いて証明していた作業を自動化し始めることができるようになるのです。

あるいはこのように定義しても良いでしょう：確率的プログラミング言語は、 rand を持つ普通のプログラミング言語に、プログラムの統計的な振る舞いを理解するのに役立つ素晴らしい多くの関連ツールを足したもの。

どちらの定義も言っていることは正しく、核となるアイデアを異なる視点から強調しているにすぎません。どちらがより納得できるかは、あなたがPPを何のために使用したいかによりけりです。ただ、目的がプログラムを動作させ、何かしらの出力を得るということになってくると、PPLで書いたソースと普通のソフトウェアのソースが多くの点で似通ってきてしまうのですが、この事実には惑わされないでください。PPの目的は分析であって、実行ではありません。

1.3. 論文推薦システムの例

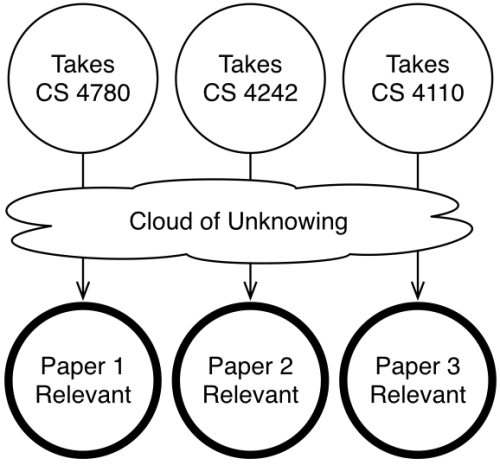
図1. 論文推薦の問題。細い線の円は観測、太い線の円は私たちが得たい出力。

例として、学生が受講した授業を基に彼らに適切な論文をリコメンドするシステムを構築しているとしましょう。物事を単純にするために、研究テーマはプログラミング言語と分析・機械学習の2つだけとし、どの論文もPLか統計学、またはその両方の論文であるとします。そして、本学（コーネル大学）で開講している確率的プログラミングに関する次の3つのクラスだけを考慮します。CS 4110（プログラミング言語）、CS 4780（機械学習）と、架空のクラスとして確率的プログラミングのための科目”CS 4242″があるとします。

この問題に機械学習が有効であろうということは、容易に想像が付きます。学生の受講スケジュールから導き出されるいくつかの集合を混ぜ合わせたものが、あなたが次に読むべき論文を演繹してくれるでしょう。しかし問題は、厳密な関係性を直接的に解決することが難しいということです。CS 4780のクラスを受講するということは、統計学により関心があるのだろう、ということを示していますが、では、正確に どのくらい 関心があるのでしょう？　CS 4780に登録をしたのは、スケジュールに合うのがこのクラスしかなかったからという場合はどうでしょう？　また架空のクラスであるCS 4242やその他の実在するクラスだけを受講する学生についてはどうでしょうか？　単純にPLと統計学を受講する学生が半々と仮定すればいいのでしょうか？

1.3.1. 問題をモデル化する

この問題に対する機械学習的なアプローチでは、いくつかが 潜在的 である 確率変数 を使って状況を モデル化 します。重要となる点は、図1の矢印は因果関係を示していないのであまり意味がないことです。CS 4110を受講するということが、任意のある論文についてより関心があるということにはなりません。両方の事象を確率的に引き起こす要因が他にあったりするわけです。この状況を説明してくれるのが確率的 潜在 変数の存在です。潜在変数の存在を理解することで、この問題を直接的に解決することを大いに手助けしてくれるでしょう。

図2. 関心がどのようにクラス登録と論文との関連性に影響を与えるかのモデル。点線の円は潜在変数で、入力または出力のどちらでもありません。

これは、統計学やプログラミング言語への各学生の関心について、いくつかの潜在変数を取り入れたモデルです。モデルについてより具体的に説明していきますが、矢印についてはすぐに意味が理解できるはずです：これらの矢印は、ある変数が何らかの形で他の変数に 影響を与えている ことを示しています。ご存知の通り学生は関心のある全てのクラスを受講するわけではないので、ここで第三の隠れた要因を考えることにします―それはどのくらいその学生が 忙しい のかという要因で、 どの クラスも受講する可能性が低いことを示します。

この図式は ベイジアンネットワーク と呼ばれるもので、各ノードが確率変数であり各エッジが統計的依存関係を表すグラフです。変数間でエッジを持たない変数は、統計的に独立しています（つまり、1つの変数に関する何かが分かっても、その他の変数の結果については何も分からない、ということを示しています）。

このモデルを完成させるために、関心についての潜在変数が論文との関連性にどのように影響するかを示してくれるノードとエッジを書いてみましょう。

図3. 残りのモデル：関心が論文との関連性にどのように影響を与えるか

基本的な考え方としては、関心を寄せている度合いや忙しさを学生に聞くということではなく、私たちが観察できることから 推論 するということです。そして、この推論された情報を我々が本当にやりたかったことのために利用します – それはつまり、任意の学生に対して論文の関連性を推測するということです。

1.3.2. 人間向けのモデル

ここまではモデル上で依存性を描画してきましたが、そろそろこれがどういう意味なのかについて具体的に見ていきましょう。通常であれば、確率変数に関連する多くの数式を書くというのが一般的な方法です。

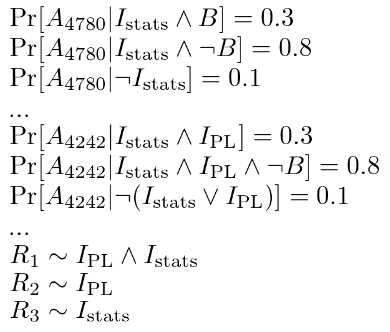
こんなにシンプルなモデルにも関わらず、多数の数式が使われてますね！しかし、難しいのはこの点ではないのです。難しくもあり役に立つ点は、私たちの観察に基づいて潜在変数を推測している 統計的推論 の部分です。統計的推論は、機械学習研究の基礎となるもので簡単ではありません。従来、専門家たちは、彼らが考案した新しいモデルのために、カスタムメイドの推論アルゴリズムを 手作業で 設計してきました。

ごく小さな実例ではありますが、統計的モデリングにおける退屈な手作業についてお分かりいただけたでしょうか。これは、アセンブリコードを書くようなものです。つまりプログラミングのようなことを行っているのですが、そこには抽象化や再利用、自己記述的な変数名、コメント、デバッガ、型システムはありません。例えば、クラス登録の方程式を見てみてください。何度も繰り返しになるので、私は全ての数式を書くのに疲れてしまいました。これは、昔ながらのプログラミング言語の抽象化であるところの関数で済ませるべきタスクであることは明らかです。PPLの目的は、すでにあなたが認識していて好んで使用している、古くて強力なプログラミング言語の不思議な力を統計学の世界に適用することにあります。

基本的なコンセプト

確率的プログラミング言語の基本的なコンセプトを紹介するために、JavaScriptで実装されたPPLである webppl と呼ばれるプロジェクトを使用しましょう。この言語について詳しく知りたい方は、スタンフォード大学の Noah Goodman と Andreas Stuhlmüller によって現在執筆されている 『The Design and Implementation of Probabilistic Programming Languages』（確率的プログラミング言語の設計と実装） をご覧ください。この言語は、ブラウザですぐに使用することができるので、入門編として使用することができます。

2.1. ランダムプリミティブ

ある言語を確率的プログラミング言語（PPL）たらしめる最も重要な特徴は、乱数を演算するプリミティブでが存在することです。この点において、PPLは rand を呼び出す従来の命令型言語によく似ています。以下は、非常に退屈なwebpplプログラムです。

var b = flip(0.5);
b ? "yes" : "no"

この退屈なプログラムは、コインを投げて表か裏のどちらが出るかを観察し、その結果を2種類の文字列どちらかを得るためだけに使います。これは、ランダムにBool値を演算するために flip 関数を呼び出すふつうのプログラムと全く同じように機能します。 基本ランダムプリミティブ(Elementary Random Primitives) と呼ばれることもある flip のような関数は、このようなプログラムでの全てのランダム性の基となっています。

webpplエディタを開いてこの小さなプログラムを動かすと、全く予想通りのことが起こるでしょう。画面には”yes”が出力されることもあれば、”no”と表示されることもあります。

webpplが個々の値だけでなく、全体の分布を表現することが分かると、若干面白さが増してくるはずです。webppl言語には Enumerate 操作があり、関数によって定義された分布全体の確率を表示します。

var roll = function () {
  var die1 = randomInteger(6) + 1;
  var die2 = randomInteger(6) + 1;
  return die1 + die2;
}

var dist = Enumerate(roll);
print(dist);
viz.auto(dist);

2と14の間にある全ての可能性のあるサイコロの値とそれらに関連する確率を出力します。また、この viz.auto の呼び出しによって、 webpplに内蔵するブラウザのインターフェース を使ってきれいなグラフを表示させています。

roll 関数を単に何度も動作させて上記 Enumerate の実装をあなたのお気に入りの言語で書くこともできるでしょうから、これを見ても何ら驚きはないかもしれません。しかし実際は、webpplの Enumerate はもう少し強力です。分布の近似値を得るためにサンプリング実行しているのではなく、正確な分布を得るために、 全ての可能性のある 関数の 実行 を列挙しているのです。このあたりから確率的プログラミング言語の核心が明らかになっていきます：それはつまり、PPLプログラムを 分析する ツールが重要なのであって、プログラムを直接実行すること自体にポイントがあるわけではないのです。

2.2. webpplで記述したモデル例

ここまでの理解があれば、論文推薦モデルの計算式は十分実装できます。各論文との関連性とクラス履修状況をそれぞれひとまとめにする関数を書き、「学生のプロファイル」をランダムに生成することこのモデルを検証してみましょう。

// Class attendance model.
var attendance = function(i_pl, i_stats, busy) {
  var attendance = function (interest, busy) {
    if (interest) {
      return busy ? flip(0.3) : flip(0.8);
    } else {
      return flip(0.1);
    }
  }
  var a_4110 = attendance(i_pl, busy);
  var a_4780 = attendance(i_stats, busy);
  var a_4242 = attendance(i_pl && i_stats, busy);

  return {cs4110: a_4110, cs4780: a_4780, cs4242: a_4242};
}

// Relevance of our three papers.
var relevance = function(i_pl, i_stats) {
  var rel1 = i_pl && i_stats;
  var rel2 = i_pl;
  var rel3 = i_stats;

  return {paper1: rel1, paper2: rel2, paper3: rel3};
}

// A combined model.
var model = function() {
  // Some even random priors for our "student profile."
  var i_pl = flip(0.5);
  var i_stats = flip(0.5);
  var busy = flip(0.5);

  return [relevance(i_pl, i_stats), attendance(i_pl, i_stats, busy)];
}

var dist = Enumerate(model);
viz.auto(dist);

これを動作させると、観測データ全体の分布が分かります。この結果自体はあまり役に立ちませんが、しかし興味深いものではあります。例えば、ある学生について 何も情報がない ときには、モデルは、学生がどのクラスもとらず、どの論文にも興味を示さない可能性が非常に高いことを示します。

2.3. 条件付け

PPLの次に重要な部分は、 条件付け 構成です。条件付けを使えば、プログラム内のある実行にどれぐらいの重みを付けるか判断することができます。決定的に重要な点は、ある実行の重みを、動作の途中、つまり計算の一部を行った後に選択できることです。さらに、ある実行を 全く無関係 としてマークし、その実行を、あるサブセットに効果的にふるい分けることさえできます。

この条件付け操作は、観察結果をコード化するために特に有用です。ある処理の結果に関して知っていることがあれば、観察結果が真実（または、真実でありそう）であることを、条件付けを使って伝えることができます。不自然な例として挙げたサイコロの例に戻りましょう。最初のサイコロが見えて、それが4だったとします。この情報に基づいて条件付けを行うと、サイコロの1つが4であったときの合計値の分布が分かります。

var roll = function () {
  var die1 = randomInteger(6) + 1;
  var die2 = randomInteger(6) + 1;

  // Only keep executions where at least one die is a 4.
  if (!(die1 === 4 || die2 === 4)) {
    factor(-Infinity);
  }

  return die1 + die2;
}

特に驚くことはありませんが、8の場合を除いて分布は平坦になります。8の場合に他の確率よりも低くなるのは、2つのサイコロで4の目が出るケースは一通りのみだからで、他のケース（通常二通り起きる）のみに比べてそれが起こる可能性は低いからです。2や12などの結果の確率はゼロです。サイコロのうち1つが4ならば、それらの結果は起こり得ないからです。

では、サイコロは見えなかったけれど、誰かがサイコロの値の合計が10だったと教えてくれたとしたらどうでしょう。このことから、サイコロそのものの値について何が分かるでしょうか。この観察を、投げた結果に条件付けを行うことによってコード化することができます。

var roll_condition = function () {
  var die1 = randomInteger(6) + 1;
  var die2 = randomInteger(6) + 1;

  // Discard any executions that don't sum to 10.
  var out = die1 + die2;
  if (out !== 10) {
    factor(-Infinity);
  }

  // Return the values on the dice.
  return die1 + "+" + die2;
}

驚くような結果ではありませんが、同じ原理を推薦システムに応用することができます。

2.4. 実際に論文を推薦する

では、同じ原理を使って実際に推薦内容を生成しましょう。簡単ですよ：対象者のクラス登録に条件付けをするだけでよいのです。私自身の例で説明しましょう。私は自分のクラスCS4110と架空のPPLクラスCS4242に参加し、MLクラス4780には参加していません。

// A model query that describes my class attendance.
var rec = function() {
  var i_pl = flip(0.5);
  var i_stats = flip(0.5);
  var busy = flip(0.5);

  // Require my conference attendance.
  var att = attendance(i_pl, i_stats, busy);
  require(att.cs4242 && att.cs4110 && !att.cs4780);

  return relevance(i_pl, i_stats);
}

（この例では、 require 関数は factor(-Infinity) をラッパーした関数として定義していて、ある条件を満たさないプログラム実行を完全に除去するように書いています。）この rec 関数を Enumerete にかけると、最終的には有用なもの、つまり論文の妥当性全体のの分布が得られます。1度に1つだけ論文を見るようにして、少し簡単に結果が見れるようにしてみましょう。

return relevance(i_pl, i_stats).paper1;

急に手際よくなった感じですね。どの 実行 が自分たちに関係あるかをenumeratorに伝えると、これらの条件下で何が分かっているか伝えてくれます。すでに私にとって、これが確率モデルを表現するためのずっと自然なツールだという気になっていますし、ほとんどのプログラマにとってもそうだと思います。プログラマは、ランダムな変数のどれが他のどれに依存しているかを注意深く記述するのではなく、プログラム実行のフローを使って依存性を構築するのです。

このセクションをまとめると、生成モデルを書くのは快適で簡単明瞭であり、プログラミング言語は生成アルゴリズムを書くための優れた方法である、ということです。このような単純（naive）なモデルについて推論を行うという重荷をコンパイラとツールに移行させることによって、仕事を楽にすることに成功しました。

2.5. 推論

この Enumerate 操作は大したものではないように見えるかも知れませんが、これこそがPPLが解決を目指す中心的問題、すなわち 統計的推論 の実装なのです。特に、条件付けが行われる場合には、一般的な確率問題の推論は難題です。 Enumerate がどのように働かなければならないか考えてみて下さい：この操作は、プログラムのランダムプリミティブの描画の 1つ1つの評価 について、プログラムの結果を知る必要があります。結果が指数関数的に増加するのは容易に想像が付きます。浮動小数点数を導入した場合には、さらに評価が不明瞭になります：0.0と1.0の間の数を描画すると、可能性のある評価が多数存在し、ヒストグラムとしては表現されません。

Enumerate はささやかではない問題には向いていません。PPLのための効率的な推論アルゴリズムがコミュニティ内で多くの関心を集めているのは、この理由によります。ここではプログラムの起こり得るすべての実行を伴わない、他の推論アルゴリズムもいくつか紹介します。

2.5.1. 棄却サンプリング法（Rejection Sampling）

Enumerateの次によく使われる推論アルゴリズムは サンプリング です。この方法では、まずプログラムを何回も動作させて、実行ごとにランダムプリミティブのそれぞれに、異なるランダムな値を演算していきます。次にプログラムの条件付けを各サンプルへの重み付けに適用して、すべてを合計します。この方法における重み付けをするインタラクション部分が本方式を棄却サンプリングと決定づけているわけですが、 棄却サンプリング という呼称は、条件次第でいくつかの実行を棄却することに由来しています。

webppl言語では組み込で本方式をサポートしています。 ParticleFilter と呼ばれるもので、前述の例で動作させることができます。

var sampled = ParticleFilter(rec('paper1'), 1000);

2.5.2. MCMC

棄却サンプリングは小規模な例には適していますが、条件付けが存在することによって問題が起こります。無関係なサンプルを採取するという（つまり、 factor 呼び出しを受けた時には棄却される運命が決まっている）無駄な作業をたくさん行うのです。もっと賢いサンプリング方法もあります。その代表は、 マルコフ連鎖モンテカルロ法 です。

webppl標準ライブラリには MCMCアルゴリズムがあります 。PPLの研究ではMCMCを正確で効率的なものにすることは人気のある課題ですが、詳細な解説は今のところ、この講義の範囲から外れています。

3. 適用例

思いっきり夢想家になってみれば、PPが約束してくれることは、機械学習の民主化に他なりません。まだ信じられない人のために、人気のある確率的プロブラミングの適用例を挙げておきます。

• TrueSkill は、おそらく最も広く言及されている例で、元々は このESOP 2011の論文 に提示されたものです。Xboxゲームの複数プレイヤーが、プレイヤーの良い組み合わせを見つけるために使うモデルです。その概念は、プレイヤーの技量の潜在変数をモデリングして、予想される勝率が50/50に近くなるようにプレイヤーを組み合わせることです。
• The webpplの書籍には巧みなコンピュータビジョンのデモがあって、生成的「順方向」モデルを「逆方向」に使用しても相補性問題をどのように解決できるかが示されています。
• Forest は、認知とNLPからドキュメント検索までの分野にわたるPPLで記述された生成モデルの、目もくらむほどのリソースです。
• まだ適用例にはなっていませんが、 Gamalon は、 Lyric Semiconductor のBen Vigoda、 Noah Goodman などが設立した新進スタートアップで、確率的プログラミングに注力していると思われます。
• そして、私の好きな適用例は、確率を取り扱う普通のプログラムを理解することです。確率的な振る舞いを取り扱う普通のソフトウェアがたくさんあります。
  • 近似計算
  • センサの取り扱い
  • セキュリティ/難読化

4. 技法

このセクションでは、確率的プログラミングに注目しているプログラミング言語コミュニティの最近の研究の例をいくつか説明します。

4.1. 確率的表明

講義の冒頭で、確率的プログラミングとは、実際に実行したい実物のソフトウェアを書くことではない、と言いましたが、PPL研究の成果を確率的な振る舞いを有する普通のプログラミングに適用するために、いくつかの研究が行われています。

私自身が手がけた、ある プロジェクト では、この原理を、統計的に振る舞うソフトウェアの正しさの制約を表現するために役立てました。その概念は、 確率的表明 である written passert を導入して、見馴れた assert 文を一般化し、確率的に動作させることです。このプロジェクトの目標は、次のとおりです。
* 複雑なプログラムに実世界のプログラミング言語（ここではLLVMプログラムなので、CとC++を考えてください）で取り組む。
* 出力の統計的チェックを高速化する。近似プログラムの品質閾値を考える。
* 条件付けを考慮しない。通常のソフトウェアに factor 文は不要であり、これにより、 passert をチェックする作業が単純化される。

4.2. R2

R2は、Microsoftが提供する確率的プログラミング言語と実装です。このツールは ダウンロード可能 です。

R2の特に優れたコンポーネントに、従来のPLの概念を適用して統計的推論を改善するというものがあります。注目すべき点は、R2のユーザが最も弱い前提条件分析(Weakest Preconditions Analysis)を使用して、前述した単純なランダム化推論方法である棄却サンプリングを改善しているということです。

WP(Weakest Preconditions)手法は、条件付けの最も苛立たしい面、つまり、山ほど作業した 後 で、それを全部捨てなければならないことが判明する、という問題を解決します。

var die1 = randomInteger(6) + 1;
var die2 = randomInteger(6) + 1;

// Discard any executions that don’t sum to 10.
var out = die1 + die2;
require(out === 10);

前述したこの部分では、プログラムの後ろの方で条件付けを行いますが、単純（naive）な方法を使っている場合には非効率的です。（ここは少し我慢して読み進め、2行目から最後の行までの追加部分が高コストであると思ってください）。表明をプログラムの早期で行うようにすると、このプログラムを改善できます。実際、そのことがWP分析の本質であり、 プログラムの後の時点Bで別の属性が真であるためにはプログラムの時点Aで何が真でなければならないか を問います。私たちの例では、条件を「上に移動させて」、条件を満たさないものを早くはじくようにすることができます。

var die1 = randomInteger(6) + 1;
var die2 = randomInteger(6) + 1;

require((die1 == 3 && die2 == 7) || ...);
var out = die1 + die2;

幸運に恵まれれば、プリミティブなサンプリング呼び出しに条件を 戻し入れ て、結局は後で棄却される作業を全く行わずに済みます。

4.3. PLの概念をPPに移植する

確率的プログラミングは、標準的なPLの文献から、その概念をPPLの世界に「移植」できるはずだ、ということも約束してくれます。その例をいくつか挙げておきます。
* 静的解析 ：表明を提供する
* 終了チェック
* プログラムの切り分け
* プログラムの統合