(編注：2020/08/18、いただいたフィードバックをもとに記事を修正いたしました。)
(2016/12/11、いただきましたフィードバックをもとに翻訳を修正いたしました。)

H.264は、動画圧縮コーデックの標準規格です。ネット上の動画、Blu-ray、スマホ、セキュリティカメラ、ドローンなどなど、今やあらゆるところでH.264が使われています。

H.264は注目すべき技術のひとつです。たったひとつの目標、つまりフルモーションビデオの送信に要するネットワーク帯域を削減することを目指した30年以上の努力の結晶なのです。

技術的な面でも、H.264はとても興味深い規格です。この記事では、その一部について概要レベルでの知識を得られることでしょう。あまり複雑だと感じさせないようにするつもりです。今回おはなしする概念の多くは動画圧縮全般にあてはまるものであり、H.264に限ったものではありません。

そもそもなぜ圧縮するのですか？

未圧縮の動画ファイルは、各フレームのピクセルデータの二次元バッファをまとめた配列になります。つまり、三次元（二次元の空間座標と一次元の時間座標）のバイト配列になるということです。ひとつのピクセルを表すには3バイトが必要になります（光の三原色である赤・緑・青についてそれぞれ1バイトを使います）。

1080p @ 60 Hz = 1920x1080x60x3 => 生データのサイズは、 約370MB/秒

これをそのまま扱うのはまず不可能でしょう。たった2分の動画でも、50GBのブルーレイディスクに収まらなくなってしまいます。ファイルをどこかに移動させるのもたいへんです。こんなデータをRAMからディスクに落とそうとすると、たとえSSDを使っても問題が発生します *1 。

なので、圧縮が必要になるのです。

なぜH.264で圧縮するのですか？

その質問にお答えする前に、まずこれを見てください。アップルのホームページです。

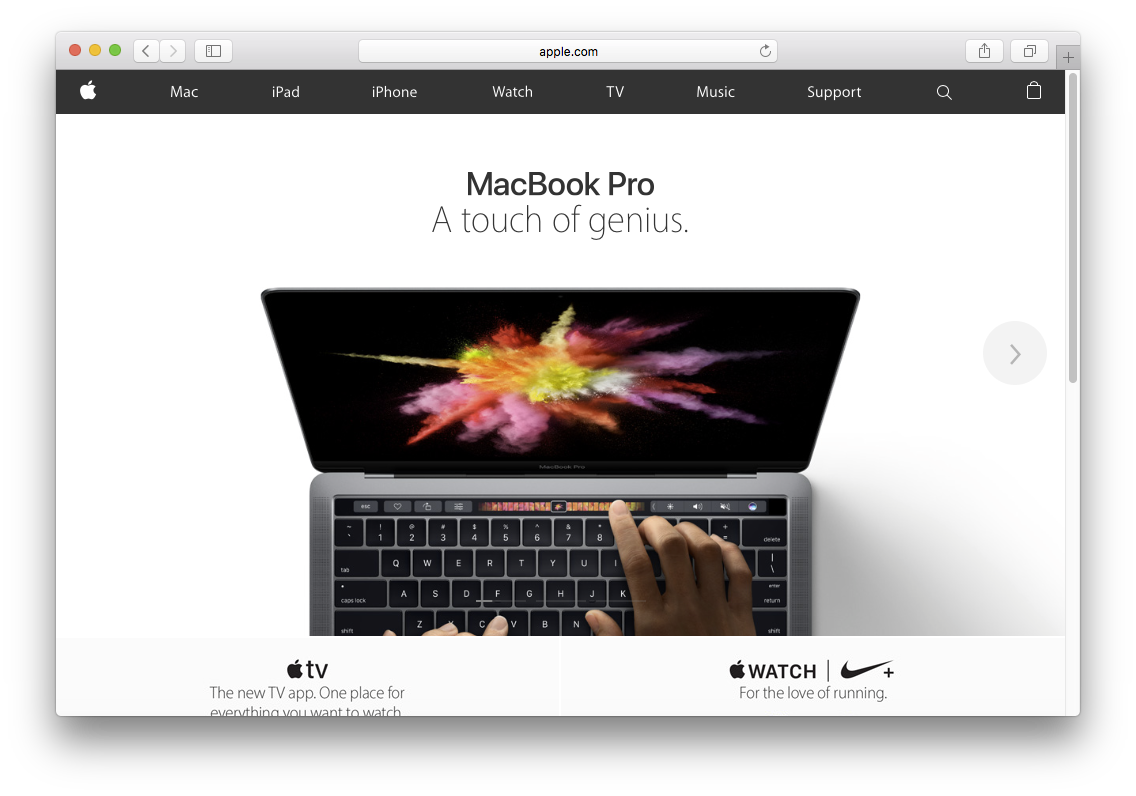
この画面をキャプチャして、ふたつのファイルを作ってみました。

• PNG形式のスクリーンショット 1015KB
• 同じページを60fpsで5秒間のH.264動画にしたもの 175KB

え、ちょっと待って。ファイルサイズ、逆じゃないですか？

いいえ、これで正しいです。300フレームのH.264動画のサイズが175KBで、その動画の1フレームをPNGに切り出すと1015KBになります。

動画のほうでは300回のキャプチャをしているのに、ファイルサイズは1/5になりました。つまり、H.264はPNGにくらべて1500倍も効率的だということです。

そんなのありえないでしょう。どんなトリックを使ったんですか？

そりゃもうトリックだらけですよ！H.264は、思いつく限りのあらゆるトリックを使っています（あと、たぶんみなさんが思いもよらないトリックもたくさん使っているでしょうね）。その中でも重要なものについて、これから説明します。

ウェイトを落とす

レーシングカーを作っているとしましょう。少しでも速く走らせる必要があります。まず何をするかといえば、重さを減らすことを考えるでしょう。現在の車両重量は1.36トンです。要らないものはどんどん捨てていきましょう。バックシート？そんなの要りませんね。サブウーファー？さようなら。音楽なんて聴きません。エアコン？外しちゃいましょう。トランスミッション？要らな……ちょっと待った！さすがにこれは外せませんね。

このように、必要なもの以外はすべて取り外します。

不要なビットを削除してサイズを減らす考えかたを、非可逆圧縮といいます。H.264は 非可逆 コーデックです。あまり重要でないビットは削除して、重要なビットだけを残します。

PNGは 可逆 コーデックです。つまり、圧縮しても何も失わないということです。PNG形式の画像からは、元のデータをビット単位で完全に復元できます。

重要なビット？動画のどのビットが重要かなんて、どうやって判断するのですか？

画像をトリミングする自明な方法なんてありません。たとえば、画像の右上部分は未使用だとみなせる場合もあるかもしれません。そんな場合なら、そこはすべてゼロだということにして、その部分の情報を切り捨てることもできるでしょう。これで、必要なスペースは3/4になります。1トンまで減らせました。あるいは、画像の周辺部分を切り取ってしまう手もあるかもしれません。重要なものがそんな端っこにあることはないでしょうからね。などなど、いろいろな手段が考えられます。しかしH.264が使うのは、そんな方法ではありません。

じゃあH.264は、どんな処理をしているのですか？

H.264は、他の非可逆画像圧縮アルゴリズムと同様に、細かい情報を切り捨てています。元の画像と切り捨てた後の画像を、拡大してみました。

圧縮後の画像では、MacBook Proのスピーカーグリルの穴が見えなくなっていることがわかります。拡大しなければ、その違いにすら気づかなかったのではないでしょうか。右側の画像のサイズは、なんと元画像のたった 7% です。これはまだ、昔ながらの意味での「圧縮」処理を施してすらいない段階ですよ。車両重量がたったの90kgになったと思うと、すごいことですよね！

7%ってすごい！どうやって細かい情報を切り捨てたのですか？

それを説明するには、少し数学の知識が必要になります。

情報エントロピー

さあここからが本番ですよ！情報理論の授業を受けたことのある人なら、情報エントロピーのことを覚えているでしょう。情報エントロピーとは、何らかの情報を表すために必要なビット数のことです。何らかのデータセットのサイズそのものを表すものではないことに注意しましょう。そのデータセットに含まれうる情報を表現するために、最低限必要なビット数を表すものです。

たとえば、コインを1回投げてどちらの面が出たかという結果を表すデータなら、必要な情報エントロピーは1ビットです。2回投げた結果を記録するなら、2ビット必要になるでしょう。ここまでだいじょうぶですか？

奇跡的に、10回投げて全部オモテが出たとしましょう。それを誰かに伝えるときに、あなたならどう言いますか？「オモテが出てオモテが出てオモテが出てオモテが出てオモテが出てオモテが出てオモテが出てオモテが出てオモテが出てオモテが出ました」なんて言わずに、きっと「10回投げて、ぜんぶオモテが出ました」と言うでしょう。ほら！たった今、あなたもデータを圧縮したわけですよ。これでつまらない講義の時間を省けました。簡単ですね。単純化しすぎていることは認めますが、何らかのデータを別の短い形式に変換して、元と同じ情報を維持したわけです。これを、データの 冗長性 を下げたといいます。このデータセットの情報エントロピーは変わっていません。単に、表現方法を変えただけです。この手のエンコーダーのことを エントロピー符号器 と呼びます。これは汎用的な可逆符号器で、画像に限らずあらゆる種類のデータで使えます。

周波数領域

情報エントロピーについて理解できたところで、データ変換に進みましょう。データは、いくつかの基本単位で表現できます。二進表現なら、0と1を使います。十六進なら16種類の文字があります。これらふたつの表現を切り替えることは簡単です。二進形式だろうが十六進形式だろうが、本質的に同じというわけです。ここまでだいじょうぶですか？では続けましょう。

さて、時間や空間によって変化する任意のデータセット（画像の輝度など）を、別の座標空間に変換できるものとします。ここでは、XY座標のかわりに、周波数座標を使うことにしましょう。X軸とY軸ではなく、freqX軸とfreqY軸を利用する座標空間です。この表現方法を、 周波数領域 表現と呼びます。この表現に関する難しい定理 *2 があります。それによると、あらゆるデータをこの形式で表現できて、freqXとfreqYが十分高ければ完全な可逆変換ができるとされています。

なるほど。で、freqXとfreqYの「freq」って何ですか？

freqXとfreqYは単位基準のひとつです。十六進から二進への変換と同様に、おなじみのXY座標からfreqXとfreqYに変換することができます。先ほどの画像を周波数領域で表すと、このようになります。

先ほどの画像におけるMacBook Proのグリル部は、周波数成分の高い情報を持っています。コンテンツが細かく変化する場合は、周波数成分が高くなります。色と明るさが徐々に変化する場合（グラデーションなど）は、周波数成分が低くなります。そして、すべての情報が両者の間のどこかにおさまります。細かく切り替わる場合が高周波数で、グラデーションが低周波数。わかりましたか？

周波数領域表現において、周波数成分の低い部分は中央に近づきます。逆に、周波数成分が高い部分は画像の周辺部分に近づきます。

なんとなくわかりました。でもいったいなぜそうするのですか？

周波数領域に変換してその周辺部分をマスクすれば、周波数成分の高い情報を切り捨てることができます。それを再びx-y座標に戻すと、元の画像に似ているけれども詳細部分が切り捨てられた画像が得られます。しかしこの画像は、元の画像に比べてサイズが小さくなりました。マスクする範囲を調整することで、どの程度の情報を切り捨てるかを細かく調整できるようになりました。

先ほどのラップトップの拡大図を改めて見てみましょう。今回は、円形のマスクを施しています。

下の数値は、元画像と比較した各画像の情報エントロピーを表します。2%まで落としても、このレベルまで拡大しなければ違いに気づかないでしょう。2%ですよ！車両重量がついに27kgになってしまいました！

ここまでが、サイズを落とす方法の説明でした。非可逆圧縮におけるこの処理のことを 量子化 *3 と呼びます。

おみごと。それ以外にはどんなことをするのですか？

クロマサブサンプリング

人間の目や脳のシステムは、細かな色の詳細をあまりうまく識別できません。明暗の細かい差は識別できるのですが、色の識別はそれほど得意ではないのです。これを利用すれば、色の情報を落としてさらにサイズを小さくできるはずです。

テレビの信号は、R+G+Bの色データをY+Cb+Crに変換しています。Yは輝度（本質的には、白黒データにおける明度）で、CbとCrは色差成分です。RGBとYCbCrの情報エントロピーは同じです。

何でまた話をややこしくするんですか。RGBではだめなんですか？

カラーテレビがうまれる前の世界には、Y信号しか存在しませんでした。カラーテレビの登場に伴って、エンジニアはY信号とRGB色情報をあわせて送る方法を考える必要に迫られました。ふたつを別々のデータストリームで送るかわりにエンジニアたちが選んだのは、色情報をCbとCrに変換したものをYとあわせて送る方法でした。この方法なら、白黒テレビは単にY成分だけを見ればいいことになります。カラーテレビは、それに加えて色差成分も見たうえで、内部的にRGBに変換しています。

ここでひとつトリックがあります。Y成分はフル解像度で符号化されているのですが、C成分はどちらも1/4の解像度でしか符号化していません。人間の目が色差の検出を苦手としているので、これで十分やっていけるのです。これで、必要な帯域はさらに半分になりました。見た目の違いはほとんどありません。半分ですよ！車両重量はいよいよ13.5kgにまで減ってしまいました。

ここでお話した色情報の切り捨て処理のことを、 クロマサブサンプリング *4 と呼びます。これはH.264に特有のものではなく何十年も前から存在する技術で、あらゆるところで用いられています。

ここまでが、非可逆圧縮におけるサイズの削減で大きなウェイトを占める処理でした。細かな変化をほぼ切り捨てた上に、色情報も半分にできたので、動画の各フレームのサイズはかなり小さくなりましたね。

それ以外に何かできるのですか？

はい。ここまでの処理は第一段階に過ぎません。ここまは、単一のフレームにおける空間領域だけしか見てきませんでした。次は、時間方向の圧縮について考えます。つまり、ここからは、時間をまたがる複数のフレーム群について考えることになります。

動き補償

H.264は、動き補償圧縮の標準規格です。

動き補償？それって何ですか？

テニスの試合を見ているとしましょう。カメラのアングルは固定されているものとします。動いているのは、行き来するボールだけです。さあ、この情報をどうやって符号化すればいいでしょうか？いつもどおりのことをやるだけですよね？二次元の空間情報と一次元の時間情報を持つ、ピクセルデータの三次元配列を扱えばいいのですよね？ほんとうに？

いや、そんな必要はありませんよね？画像の大半の部分は、変化しません。コートもネットも観客も、どれも動きはありません。実際に動いているものといえば、ボールだけです。だったら、動かない部分だけをまとめた一枚の画像を背景として用意して、ボールだけを動かした動画を用意すればよさそうです。これで、サイズをかなり減らせそうな気がしませんか？なんとなく先が見えてきたでしょう？そう、動き探索です。

実際にH.264が行っているのは、こんな処理です。H.264は、画像を複数のマクロブロックに分割します。このマクロブロックは通常は16×16ピクセルのブロックで、これを用いて動き探索を行います。まず、 Iフレーム （イントラフレーム）と呼ばれる静止画像をひとつ作ります。これはフルフレームで、画像をつくるために必要なすべてのビットの情報を含みます。それ以降のフレーム群は、 Pフレーム （前方向予測フレーム）と Bフレーム （双方向予測フレーム）のいずれかになります。Pフレームは、前のフレームからの各マクロブロックの動きベクトルを符号化したフレームです。つまり、Pフレームを復号するには、その前のフレームの情報が必要になります。デコーダは、動画ストリームにおける直近のIフレームまでさかのぼって、それ以降のすべてのフレームを順にたどり、動きベクトルの差分を積み重ねる作業を現在のフレームまで続けます。

Bフレームはもう少しおもしろいもので、過去と未来の双方向のフレームを用いた予測を行います。これで、アップルのホームページがなぜあれほどまでに圧縮できたのかが想像できるでしょう。あの動画にはたった三つのIフレームしか存在せず、そのマクロブロックをパンしているだけだったのです。

動きベクトルの差分だけしか符号化していないので、このテクニックはあらゆる動画にうまく適用できます。

これで、空間と時間の両面での圧縮をカバーできました！ここまでは、まず量子化によってサイズを節約しました。さらに、クロマサブサンプリングを用いて必要なサイズを半減させました。これらに加えて動き補償を用いることで、先ほどの動画の300フレームのうちたった3フレームだけを格納すれば済むようになりました。

私としてはこれで十分満足ですけど、まだどうにかできるんですか？

では、最後の仕上げといきましょう。昔ながらの可逆エントロピー符号器を用います。使わない理由がありませんね。

エントロピー符号器

可逆圧縮処理の後のIフレームには、冗長な情報が含まれています。PフレームやBフレームにおけるマクロブロックの動きベクトルには、まったく同じ値を持つグループがあります。なぜなら、先ほどの動画でパンするときには、複数のマクロブロックが同じ量だけ移動するからです。

エントロピー符号器が、この冗長性をうまく処理してくれます。これは汎用的な可逆符号器なので、何かとのトレードオフを気にする必要はありません。すべてのデータを元どおりに復号できるのです。

これでできあがり！これが、H.264の動作原理の核心となるトリックです。

すばらしいですね！ところで、あの自動車の車両重量は結局どこまで落ちたんでしょうね。

元の動画は1232×1154というちょっと変な解像度でした。計算してみると、こうなります。

5 secs @ 60 fps = 1232x1154x60x3x5 => 1.2 GB
圧縮後の動画 => 175 KB

1.36トンの自動車に置き換えてみると、最終的に 0.18kg まで落とせたことになります。たったの180グラムですね！

いやあ、ほんとにすごいですね！

言うまでもありませんが、この記事は、数十年にわたる研究の成果をかなり単純化したものです。もっと知りたくなったら、 Wikipediaのページ に詳しい説明があるので読んでみましょう。

「そこ、違うよ！」とか何か言いたいことがあるかたは、 HackerNews や Reddit からぜひコメントをください。

あるいは Twitter や LinkedIn からつっついてもらってもかまいません。

[*1] SSDのベンチマーク

[*2] ナイキスト・シャノンの標本化定理

[*3] 量子化

[*4] クロマサブサンプリング