(注：2017/04/08、いただいたフィードバックを元に翻訳を修正いたしました。 @liaoyuanw )

この記事は、私の著書 『Deep Learning with Python（Pythonを使ったディープラーニング）』 （Manning Publications刊)の第9章2部を編集したものです。現状のディープラーニングの限界とその将来に関する2つのシリーズ記事の一部です。

既にディープラーニングに深く親しんでいる人を対象にしています（例：著書の1章から8章を読んだ人）。読者に相当の予備知識があるものと想定して書かれたものです。

ディープラーニング：　幾何学的観察

ディープラーニングに関して何より驚かされるのは、そのシンプルさです。10年前は、機械認識の問題において、勾配降下法で訓練したシンプルなパラメトリックモデルを使い、これほど見事な結果に到達するなど誰も想像しませんでした。今では、 十分に多い 事例に対する勾配降下法で訓練した、 十分に大きな パラメディックモデルさえあればよいのです。かつてFeynmanが宇宙を指して言ったように、 「複雑ではない、ただ量が多いだけ」 なのです。

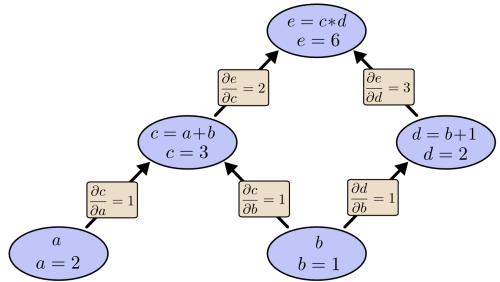
ディープラーニングにおいて、すべてはベクトルです。すなわち、すべては幾何学的空間における点なのです。モデルのインプット（テキスト、画像など）とターゲットはまず、「ベクトル化」されます。つまり、始点のインプットベクトル空間とターゲットベクトル空間になるということです。ディープラーニングのモデルの各レイヤーは、通過するデータに対して1回の単純な幾何学的変換を実行します。これが組み合わされることで、モデルのレイヤーの連鎖が１つの非常に複雑な幾何学的変換を形成します。これは連続するシンプルな変換に分割できます。この複雑な変換は、一度に１点ずつ、入力空間を終点空間へマッピングしようとするものです。変換はレイヤーの重みによってパラメータ化され、重みはその時点のモデルの性能評価に基づいて繰り返し更新されます。この幾何学的変換の大きな特徴は微分可能であることで、これは勾配降下法を用いてパラメータを学習するために必要とされます。直感的に言えば、入力から出力への幾何学的変形が滑らかかつ連続的でなければならないということです – 大きな制約です。

この複雑な幾何学的変換を入力データに適用する全体のプロセスは、立体的に視覚化できます。紙のボールのしわを伸ばそうとしている人を想像してください。紙を丸めたボールは、モデルの始点となる入力データの多様性を表します。人が紙のボールに施す各動作は、1つの層が操作するシンプルな幾何学的変換に似ています。ボールをほどくしぐさの最初から最後までの連続は、モデル全体の複雑な変換です。ディープラーニングモデルは高次元データの複雑な多様体をほどくための数学的機械なのです。

それこそがディープラーニングの魔法です。意味をベクトル、幾何学的空間に変換した後、ある空間を別の空間にマッピングする複雑な幾何学的変換を段階的に学習するのです。必要なのは、元のデータにある関係性の全範囲を取得できる、十分に高い次元を持つ空間だけです。

ディープラーニングの限界

このシンプルな戦略で実装できるアプリケーションの空間はほとんど無限大です。けれども、もっと多くのアプリケーションは完全に現状のディープラーニング技法の範囲外にあります – たとえ、人間がアノテーションを加えたデータがどれだけ大量にあったとしても。たとえば、プロダクトマネージャーが書くような、ソフトウェア製品の機能を英語で記述した仕様書を何十万件 – さらには何百万件 – も集めて、データセットを作成することはできるでしょう。また、これらの要件を実現するようエンジニアチームが開発したソースコードを、それぞれ仕様書に対応づけることも可能でしょう。しかし、このデータをもってしても、単に製品仕様書を読んだだけで適切なコードベースを生成するようディープラーニングモデルを訓練することはできないのです。これは数多くあるうちのほんの一例です。一般に、論理的な思考（プログラミング、科学的方法の適用など）、長期的な計画、アルゴリズム的なデータ操作を必要とする問題には、ディープラーニングのモデルの力は及びません – たとえ、どれほどのデータを入力しても。ディープニューラルネットワークを使ってソートアルゴリズムを学習することさえ、途方もなく困難なのです。

理由は、ディープラーニングモデルは、「単に」あるベクトル空間を別のベクトル空間にマッピングする シンプルで連続的な幾何学的変換の連鎖 でしかないからです。できるのは、1つのデータ多様体Xを別の多様体Yにマッピングすることだけです。その際、XからYへの学習可能な連続変換が存在し、トレーニングデータとして使用するためのX：Yの高密度サンプリングが利用可能であると仮定しています。したがって、ディープラーニングモデルを一種のプログラムとして解釈することはできても、逆に ほとんどのプログラムはディープラーニングモデルとして表現できません。 ほとんどのタスクにおいて、タスク解決に対応する実際的なサイズのディープニューラルネットワークが存在しないか、存在する場合でも学習可能ではないからです。つまり、対応する幾何学的変換があまりに複雑過ぎるか、それを学習するための適切なデータがないといった状況です。

より多くのレイヤーを積み重ねたり、より多くの訓練データを使用して現状のディープラーニング技法をスケールアップしても、問題のごく一部を表面的に緩和させられるに過ぎません。データを増加させたとしても、ディープラーニングのモデルが表現できることは非常に限られているという根本的な問題を解決できません。また、学習させたいと思うプログラムの大半は、データ多様体の連続的な幾何学的変形として表せないという問題も解決できません。

機械学習モデルを擬人化するリスク

現代のAIに関する非常に現実的なリスクの1つとして、ディープラーニングモデルの機能を誤って解釈し、その能力を過大評価することが挙げられます。人間の精神の根本的な特徴には、「心の理論」があります。私たちの周囲のものに意図、信念、知識を投影する傾向です。石にスマイルマークを描くと、突如としてそれは「ハッピーな石」になります。- 私たちの心の中で。ディープラーニングに適用されると、モデルが絵画を説明するキャプションを生成するよう何とか訓練できた場合、モデルが、キャプションを生成するのと同時に、絵の内容を「理解している」と信じ込んでしまうことを意味します。すると、訓練データに存在する画像の種類から若干のズレが生じたことによって、モデルが完全に不条理なキャプションを生成したとき、私たちは必要以上にビックリしてしまうわけです。

注釈：少年は野球のバットを持っている。

とりわけ、これは「敵対例、敵対的サンプル(adversarial examples)」において顕著に示されています。これはモデルが誤分類するよう意図的に作られたディープラーニングネットワークへの入力例です。既に気づいているかと思いますが、入力空間内で勾配上昇法を使えば、何らかの畳み込みニューラルネットワークの活性度を最大化する入力を生成できます。
これは5章（原注： 『Deep Learning with Python』 ）で紹介したフィルタの視覚化手法、8章のディープドリームアルゴリズムの基礎でもあります。同様に、勾配上昇法を使って画像をわずかに変形させれば、所与のクラスに対する分類予測を最大化できます。パンダの写真をとり、そこに「テナガザル」の勾配を追加すると、ニューラルネットワークに、パンダの写真をテナガザルと分類させられます。以上の例は、これらのモデルの脆さを示しており、また、モデルが行う入力から出力へのマッピングと人間の知覚との間にある深い差異も証明しています。

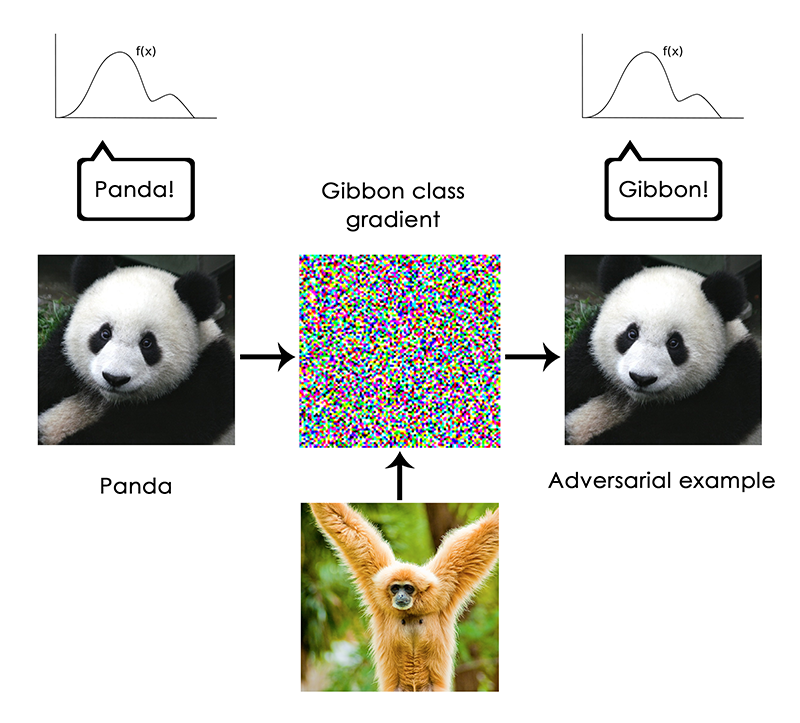
注釈：
（上行）パンダ！　テナガザルクラスの勾配　テナガザル！
（下行）パンダ　敵対的なサンプル

端的に言えば、ディープラーニングのモデルは入力を一切理解していないということです。少なくとも、人間的な意味においては。私たち自身のイメージ、音、言語の理解は、人間としての、実体を持つ地球上の生物としての感覚運動の経験に接地しています。
機械学習モデルはそういった経験へのアクセスがないゆえに、人間的な方法で入力を「理解」できないのです。膨大な訓練サンプルにアノテーションを付与してモデルに入力すれば、この特定のサンプルデータの集合については、データを人間の概念にマッピングする幾何学的変換を学習させられるでしょう。しかし、このマッピングは、単に私たちの心の中にある元のモデルの単純化されたスケッチでしかなく、それは実体ある生き物としての我々の経験から開発されたものです。鏡の中のぼやけた像のようなものです。

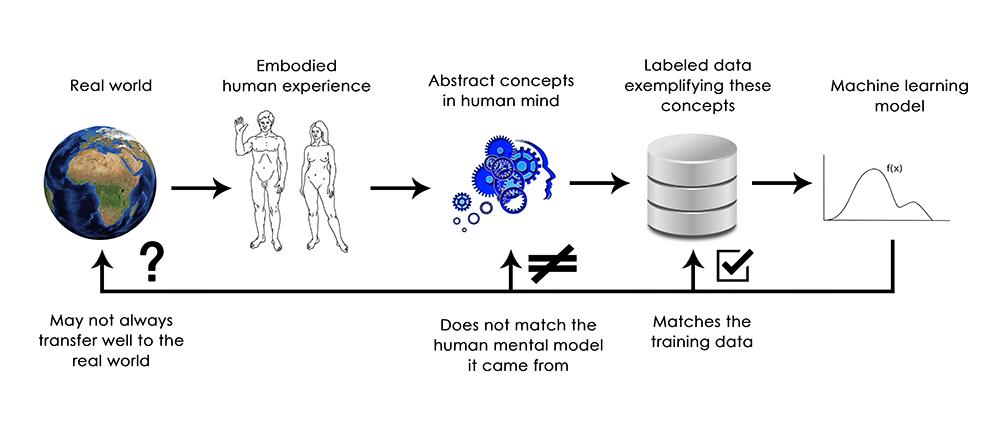
注釈：
（上行）現実世界→具体的な人間の経験→人間の心の抽象的概念→これらの概念を実証するラベル付きのデータ→機械学習モデル
（下行）常に現実世界に都合よく移行できるとは限らない
その出所である人間の精神モデルにマッチしない
訓練データにマッチする

機械学習の実践者として、常にこの事実を心に留めて、間違っても「ニューラルネットワークは実行したタスクを理解している」と信じ込まされないようにしましょう。実際、少なくとも人間が分かるような筋道では理解していないのですから。ネットワークは、私たちが教えたいと思っていたことよりもはるかに狭い範囲で、意図と異なるタスクを訓練されてきたのです。つまり、単に訓練の入力を訓練の目標に1点ずつマッピングしてきただけなのです。訓練データから逸脱したものを見せたら最後、ネットワークは信じがたいほど不条理な形で壊れるでしょう。

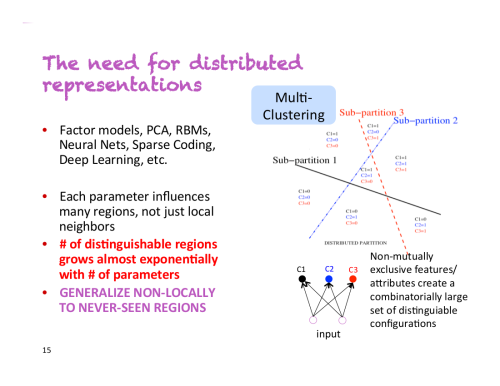
局所的一般化　対 極度の一般化

ディープラーニングモデルが行う入力から出力への直接的な幾何学的変形と、人間が考え、学習する方法との間には根本的な違いがあるようです。それは、人間が明示的な訓練のサンプルを提示されるのではなく、身体的な経験から自分自身で学ぶという事実だけではありません。学習プロセスの違いを考慮しなくとも、根本的な表現の性質にそもそもの違いがあるのです。

人間は、直接的な刺激を直接的な反応にマッピングする（ディープネットや、あるいは昆虫のように）よりもはるかに高度な処理ができます。現在の状況に関する、あるいは自分自身や他の人に関する複雑で 抽象的なモデル を維持し、これらのモデルを使用してさまざまな未来の可能性を予測し、長期的な計画を実行できるのです。人間には、既知の概念と、一度も経験がないものの表す概念を融合する能力があります。たとえば、ジーンズをはいた馬を描いたり、宝くじに当選したら何をするか想像することです。この仮説を扱う能力、直接的に経験できることをはるかに超えてメンタルモデルの空間を拡張する能力、言い換えれば、 抽象化 と 推論 を実行する能力こそ、人間の認知の特徴を定義するものだと言えるでしょう。私はこの能力を「極度の一般化」と名付けたい。つまり、非常に少ないデータを使用して、または新しいデータを全く使用せず、経験のない斬新な状況に適応する能力を指します。

これはディープネットの動作とは著しい対照をなしています。それは「局所的一般化」とでも呼べるもので、ディープネットが実行する入力から出力へのマッピングは、新しい入力が訓練時に経験したものと少しでも異なる場合、即座に意味をなさなくなります。たとえば、ロケットを月に着陸させるために、適切な発射パラメータを学習するという問題を考えてみましょう。このタスクにディープネットを使用したとすれば、教師あり学習、強化学習のどちらを利用した訓練であれ、数千から数百万回の打ち上げテストを与える必要があります。つまり、入力空間の 高密度なサンプル にさらし、信頼に足る入力空間から出力空間へのマッピングを学ばなければなりません。

対照的に、人間は自らの抽象化の力を使うことができるので、物理モデル（ロケット科学）を生み出し、わずかなテストだけでロケットを月へと送る正確な解決策を見つけられます。同様に、人間の身体を制御するディープネットを開発して、自動車に衝突せず安全に街を案内するよう学習させたい場合、自動車や危険を予測し適切な回避行動ができるまでには、ネットは様々な状況で数千回も死なねばならないでしょう。新しい街に放り込まれた場合、それまで学んできたことのほとんどを再学習する必要があります。その一方で、人間はただの一度も死ぬことなく安全な行動を学習できます。これもまた、仮説的状況を抽象化モデリングする力のおかげです。

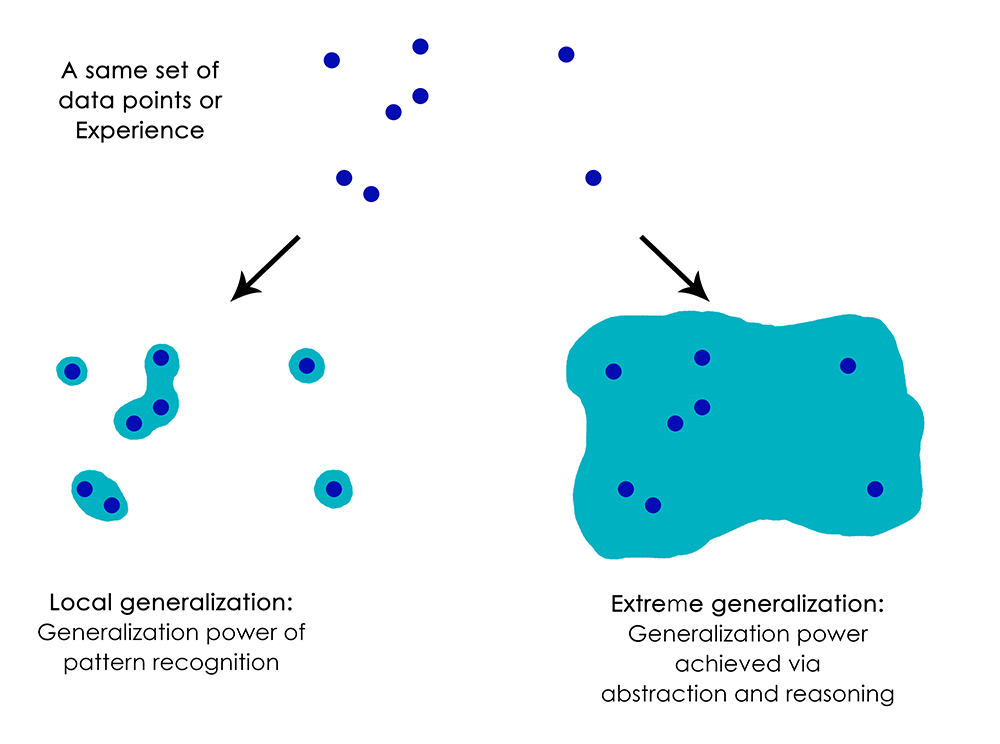
注釈：（上から）データ点や経験の同じセット
局所的一般化： パターン認識による一般化の力
極度の一般化： 抽象化と推論を経て到達する一般化の力

つまり、機械認識の進歩にもかかわらず、まだまだ人間レベルのAIには遠く及ばないということです。モデルが実行できるのは単なる 局所的一般化 であり、新しい状況が過去のデータと非常に近い場合に何とか適応するだけです。一方、人間の認知には 極度の一般化 の能力があり、全く新しい状況にも即座に適応したり、将来の状況を長期にわたって計画したりすることができます。

まとめ

次のことを覚えておきましょう。現在までのディープラーニングで唯一本当に成功していると言えるのは、人間の注釈が付いたデータを大量に与えた場合に、連続的な幾何学的変換を使用して空間Xを空間Yにマッピングする能力です。これをうまく活用すると、基本的にはどの産業界でも大変革を起こせますが、人間レベルのAIと言うにははるかにほど遠いのが現状です。

これらの制限をいくらか取り去り、人間の脳との競争を開始するためには、単純な入力から出力へのマッピングを離れて、推論と抽象化へと移動する必要があります。さまざまな状況や概念を抽象的にモデリングするための基盤として見込みがありそうなのは、コンピュータプログラムの抽象モデルではないかと思います。以前、機械学習のモデルは「学習可能なプログラム」とも定義できると述べました。（原注： 『Deep Learning with Python』 で）現時点では、可能性のあるあらゆるプログラムのうちで、非常に狭い範囲の、ある特定のサブセットに属するプログラムしか学習できません。けれども、モジュール式かつ再利用可能な方法で、あらゆるプログラムを学習できるとしたらどうでしょうか。次の記事では今後の見通しについて検討します。

2番目のパートはこちらで読めます。 『ディープラーニングの未来』