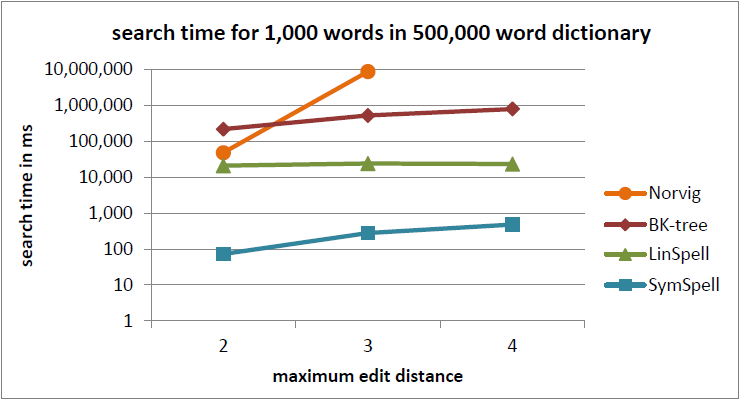
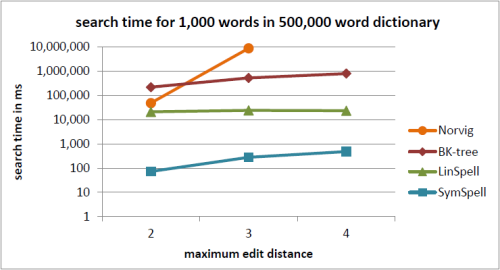
注釈：500,000単語収録の辞書内における1,000単語の検索時間
X:最大編集距離
Y:検索時間/ms

従来、スペル修正や文字列のあいまい検索には、 BK木 が適していると言われてきました。しかし、これは本当でしょうか。

また、 スペル修正に関する私のブログ に寄せられたコメントには、BK木が、あいまい検索のためのデータ構造として優れていると言及されていました。

そのような経緯から、今回、BK木と他の選択肢のベンチマークを取って比較してみようと思い立ったわけです。

近似文字列検索アルゴリズム

近似文字列検索では、文字列リスト内の文字列を検索し、特定の 文字列メトリック に従って、それに近い文字列を返します。

文字列メトリックは多数あり、例えば レーベンシュタイン距離 、 Damerau-Levenshtein距離 、 ハミング距離 、 ジャロ・ウィンクラー距離 、 Strike a match などはその一例です。

今回の記事では、 Damerau-Levenshtein の文字列メトリックに基づいて、最大 編集距離 における文字列リストの文字列を4種類のアルゴリズムで検索し、それらを比較してみたいと思います。

スペル修正の場合、各語に関連する 単語頻度 を追加で使用することで、結果（提案）を更に分類およびフィルタリングすることが可能です。

キーボードレイアウト上で近い位置にあるペア、または音が似ているペアに高い優先度を与える 重み付き編集距離 を実装することもできます（例：同じ発音の異なるスペルを識別する Soundex または他の 発音アルゴリズム ）。なお、 重み付きDamerau-Levenshtein編集距離/キーボード距離によるSymSpellの実装 がありますが、 重み付き編集距離は本記事の焦点から外れるので、多くは触れません。 お好みに応じて後処理ステップとして追加することができ、その場合、Damerau-Levenshtein編集距離でフィルタリングされた予備結果を優先順位付け/ソートすることで、ほとんどの近似文字列検索アルゴリズムに対して、パフォーマンスにわずかな向上をもたらすことができます。

全てのアルゴリズムの最終目標は検索時間を短くすること、つまり、精度を維持しながら、 ルックアップと比較の数を減らし （単語/人為的に生成された候補間）、 できる限り完全な編集距離計算の回数を減らし、 最終的に 編集距離計算自体の計算上の複雑さを軽減する ことです。

今回、比較を予定している4つのアルゴリズムを以下に挙げます。

• NorvigのSpelling Corrector
• BK木（Burkhard-Keller木）
• SymSpell （Symmetric Deleteスペル修正アルゴリズム）
• LinSpell （線形検索のスペル修正アルゴリズム）

レーベンシュタイン編集距離のバリエーション

今回の4つのアルゴリズムはどれもレーベンシュタイン編集距離から派生したものを使っています。
レーベンシュタイン距離には次の3種類 があります。

• レーベンシュタイン距離 ：隣接する転置（AC→CA）は2回の編集としてカウントされます。 三角不等式が成立します。
• 制限付きのDamerau-Levenshtein距離 （最適な文字列アライメントアルゴリズム）：隣接する転置は1回の編集としてカウントされますが、サブ文字列を複数回編集することはできません：ed(“CA” , “ABC”) =3。 三角不等式は成立しません。
• 真のDamerau-Levenshtein距離 ：隣接する転置は1回の編集としてカウントされ、サブ文字列は複数回編集することができます：ed(“CA” , “ABC”) =2。 三角不等式が成立します。

Norvigのアルゴリズムは、真のDamerau-Levenshtein 編集距離を使用しています。これを変更して、レーベンシュタイン距離を使うようにすることができます。

Xenopax の BK木 実装は、 レーベンシュタイン 編集距離を使用しています。これを変更して、真のDamerau-Levenshtein編集距離を使うようにすることができますが、 BK木に必要な三角不等式が成立しない 制限付きのDamerau-Levenshtein編集距離を使うようには変更できません。

SymSpell は、 制限付きのDamerau-Levenshtein 編集距離を使用しています。これを変更して、レーベンシュタイン距離または真のDamerau-Levenshtein距離を使うようにすることができます。

LinSpell は、 制限付きのDamerau-Levenshtein 編集距離を使用しています。これを変更して、レーベンシュタイン距離または真のDamerau-Levenshtein距離を使うようにすることができます。

検索結果の冗長性

テストでは、 ルックアップ時間の違い につながる検索結果の 冗長性を3つのレベル に区別しました。

レベル0： 最大編集距離内において、最小編集距離の結果のみを返します。同じ編集距離で複数の結果が存在する場合は、単語の頻度が最高の結果を返します。これにより、例えば編集距離=0の結果が見つかった場合などで、検索の早期終了が可能になります。

レベル1： 最大編集距離内において、最小編集距離の全ての結果を返します。同じ編集距離で複数の結果が存在する場合は、単語の頻度によりソートされた全てを返します。これにより、例えば編集距離=0の結果が見つかった場合などで、検索の早期終了が可能になります。

レベル2： 単語頻度でソートされた最大編集距離内の全ての結果を返します。この場合、検索を早期に終了することはできません。

NorvigのSpelling Corrector

Spelling Correctorの基本的な考えは、スペルを間違えた語から、最大編集距離内の全ての語を人為的に生成した場合、正しい語がそれらの中になければならないということです。それらが一致するまでは、辞書内の全てを見なければなりません。つまり、スペルの4つのエラータイプの可能な組み合わせ（挿入、削除、置換、隣接交換）が全て生成されることになり、例えば単語長=9、編集距離=2の場合、114,324もの候補が生成されるなど、コストが非常に高くなります。

これは従来、 Pythonで書かれて いました。このベンチマークでは、信頼性の高いPeter Norvigアルゴリズムの Lorenzo StoakesのC#ポート を使用しました。これは、編集距離3をサポートするように拡張されています。

BK木

BK木 は、レーベンシュタイン編集距離の特性である 三角不等式 を使用します：
Levenstein(A,B)+Levenstein(A,C)≥Levenstein(B,C)、およびLevenstein(A,B)−Levenstein(A,C)≤Levenstein(B,C)。

索引付け中 、Levenshtein(root node,child node)が事前計算されます。

ルックアップ中 、Levenshtein(input ,root node)が計算されます。 三角不等式 はフィルタとして使用され、事前計算されたLevenstein(root node,child node)が[Levenstein(input ,root node)-dmax, Levenstein(input ,root node)+dmax]の範囲内にある場合、子ノードを再帰的に追従します。

BK木を詳しく議論した興味深い記事について、以下にいくつかを挙げるので、ぜひご覧ください。

• The BK-Tree — A Data Structure for Spell Checking（BK木 – スペルチェックのためのデータ構造）
• Interesting data structures: the BK-tree（興味深いデータ構造：BK木）
• Interesting data structures: the BK-tree (HN discussion)（興味深いデータ構造：BK木（HNディスカッション））
• Damn Cool Algorithms, Part 1: BK-Trees（クールなアルゴリズム、パート1：BK木）
• BK-Tree | Introduction & Implementation（BK木 | 導入と実装）
• Implementing BK-tree in Clojure（ClojureでのBK木実装）
• BK-tree（BK木）

今回のベンチマークにおいては、以下に挙げる3つのBK木のC#実装を比較しました。

• BK木1（ tgriffithのC#実装 ）
• BK木2（ TarasRoshkoのC#実装 ）
• BK木3（ XenopaxのC#実装 ）

そして、最速だった Xenopax （これは、Wikipediaからもリンクされています）を使用することに決めました。

SymSpellアルゴリズム

SymsSpellは、短時間の間に、巨大な文字列リストから最大編集距離内の全ての文字列を見つけるアルゴリズムです。スペルチェックや文字列のあいまい検索に使用できます。

速度については、 Symmetric Deleteスペル訂正アルゴリズム に由来しており、 プレフィックス索引付け によってメモリ要件をチェックします。

Symmetric Deleteスペル訂正アルゴリズム は、所与のDamerau-Levenshtein距離に対する編集候補生成と辞書検索の複雑さを軽減します。（削除＋転置＋置換＋挿入による標準的なアプローチに比べ）100万倍の速さであり、言語にも依存しません。

他のアルゴリズムとは逆に、必要なのは削除のみで、転置＋置換＋挿入は必要ありません。入力する語の転置＋置換＋挿入は、辞書の単語の削除に変換されます。 置換や挿入は、コストが高く、言語に依存します（例えば中国語のようにユニコードの漢字が7万字もあるような場合）。

スピードは、事前計算によるところが大きいです。平均5文字の単語では、最大編集距離3以内で約300万通りのスペルミスが考えられますが、SymSpellでは25件の削除を事前計算し保存するだけでその全てをカバーできるのです。ちょっとしたマジックですね。

プレフィックス索引付け の基本的な考えは、 単語長が長くなるにつれて、追加の文字の識別の力が減少する ということです。従って、削除候補の生成を接頭辞に制限することにより、フィルタの効率をさほど犠牲にすることなく、スペースを節約できるようになります。ベンチマークでは、3つの異なるプレフィックス長lp＝5、lp＝6およびlp＝7が使われました。それらは、検索速度とインデックスサイズ間の異なる妥協点を反映しており、 プレフィックスの長くなると、大きなインデックスのサイズを犠牲にして、検索速度が向上します。

SymSpellのC#ソースコードは、GitHubのオープンソースとして公開されています 。

LinSpell

LinSpellは、基本的に（多少、調整はありますが）、単語リストを線形走査し、各単語の編集距離を計算するものです。これをベンチマークの基準指標とするつもりでした。結果を見て驚いたことは、そのO（n）特性にもかかわらず、BK木とNorvigのアルゴリズムの両方を凌駕したことでした。

それにはいくつかの理由があります。

• 大文字O表記の定数を過小評価してはいけません。BK木のノードを20％しか探索しない場合、アトミック操作のコストがわずか10％の線形検索よりもコストが高くなります。
• Damerau-Levenshteinの計算はコストが非常に高いため、重要なのは処理された単語数ではなく、Damerau-Levenshteinの完全な計算が必要な単語数です。計算する単語を事前にフィルタリングしたり、任意の編集距離に達すると同時に計算を終了したりするようにすれば、検索の速度を向上できます。
• 検索をベストマッチに制限した場合、検索の早期終了オプションを利用することができます。
• 単語はスペルミスがない場合がほとんどです。その場合、O(1)のハッシュテーブルまたはトライでルックアップを行うことができます。検索をベストマッチに制限した場合、検索を即座に終了することが可能です。
• Abs(word.Length-input.Length)＞最大編集距離（または、検索をベストマッチに制限している場合、それまでの最良の編集距離）の場合、編集距離を計算する必要はありません。
• 検索をベストマッチに制限した場合、最良の編集距離に達すると、編集距離計算を終了することができます。
• 検索をベストマッチに制限し、編集距離＝1のマッチが1つでも見つかった場合で、当該の語数がすでに見つかったマッチ数よりも少ない場合、編集距離を計算する必要はありません。

LinSpellのC#ソースコードは、GitHubのオープンソースとして公開されています 。

テストのセットアップ

4つの近似文字列検索アルゴリズム のベンチマークを実施するために、 各検索アルゴリズムに対して2*3*3+2*2のテスト を行います。

スペルミスを無作為に織り交ぜた1,000の単語 を、 2種類の辞書サイズ （29,159単語と500,000単語）、 3種類の最大編集距離 （2、3、4）そして 3種類の冗長タイプ （0、1、2）を使って検索します。各テストで、 検索の総所要時間 を測定します。

2 種類の辞書サイズ （29,159単語と500,000単語）に対しては、辞書と補助的なデータ構造を作成するために必要な 事前計算時間 と、その メモリ消費量 を測定します。

結果の完全性 を確実にするために、4つのアルゴリズムから出された結果を比較しました。アルゴリズムに使われているレーベンシュタインの種類が違うために結果が異なるという点は、考慮に入れています。

テストの焦点と制限事項

ベンチマークにおける最大編集距離は4に制限しました。自然言語の検索では、編集距離4は十分に妥当な境界線となるからです。誤検知が潜在的に大きくなるに従って、リコールはわずかになる一方で、精度は低下してしまいます。

ベンチマークで用いる辞書サイズは最大500,000単語に制限しました。これは、20巻のオックスフォード英語辞典でも、現代語は171,476語だけ、古語は47,156語だけしか収録されていないからです。

自然言語の領域を超える、長い文字列やビットベクトル（画像、声、音声、映像、DNA配列、指紋…）のあいまい検索には、より大きな編集距離と辞書サイズが必要であり、導かれる結果も異なる可能性があります。

複数語（製品やイベントデータベース）に対するあいまい検索や、より大きなテキストの断片（盗用検出）については、欠落した単語や交換された単語を説明するために、混合、分解、そして Strike a match のような、編集距離以外の文字列メトリックが必要になるでしょう。

どちらの事例も、本稿では取り上げません。

テストデータ

noisy_query_en_1000.txt

クエリには、Norvigのテキストコーパス big.txt から取得した独自の1,000の単語を使用します。

各単語に対して、レンジ0からMin（word.length /2,4）の ランダムな数の編集 が選択されます。それぞれの編集では、 ランダムなタイプの編集 （削除、 ランダムな文字 の挿入、 ランダムな文字 による置換、隣接する文字の交換）が、単語の中の ランダムな位置 に適用されます。編集後に許容される単語は、重複の無い、語長＜2のものだけです。

frequency_dictionary_en_30_000.txt

Norvigのテキストコーパスの big.txt から取得した独自の29,159の単語を、コーパス内の頻度とともに収録しています。

frequency_dictionary_en_500_000.txt

Google Books Ngramのデータ から取得した100万語の英語の単語リストから、最も使用頻度の高い500,000語を、その頻度とともに収録しています。

これら全てのテストデータファイルは、GitHubで公開されています 。

ベンチマークの結果を自身で再現したい場合、または文字列のあいまい検索のその他のアルゴリズムと比較したい場合は、 symspelldemo.cs のBenchmark()メソッドを参照してください。

ベンチマークの結果

注釈：30,000単語収録の辞書内における1,000単語の検索時間
冗長＝0
X:最大編集距離
Y:検索時間/ms

注釈：500,000単語収録の辞書内における1,000単語の検索時間
冗長＝0
X:最大編集距離
Y:検索時間/ms

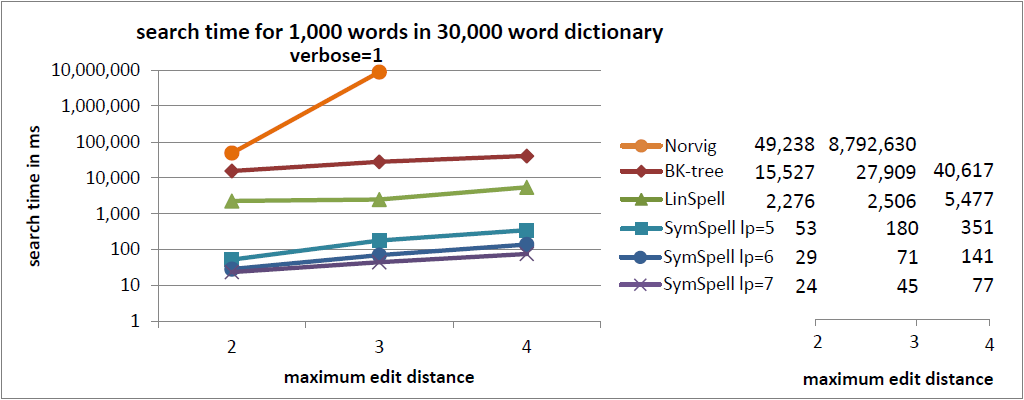
注釈：30,000単語収録の辞書内における1,000単語の検索時間
冗長＝1
X:最大編集距離
Y:検索時間/ms

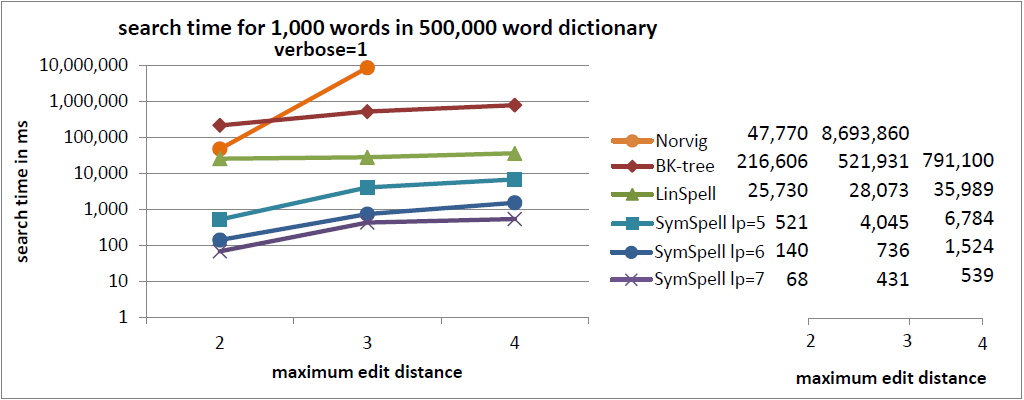
注釈：500,000単語収録の辞書内における1,000単語の検索時間
冗長＝1
X:最大編集距離
Y:検索時間/ms

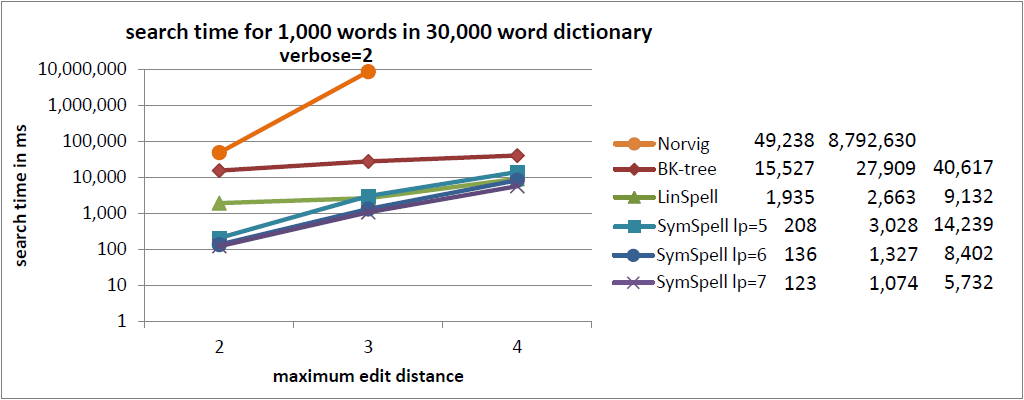
注釈：30,000単語収録の辞書内における1,000単語の検索時間
冗長＝2
X:最大編集距離
Y:検索時間/ms

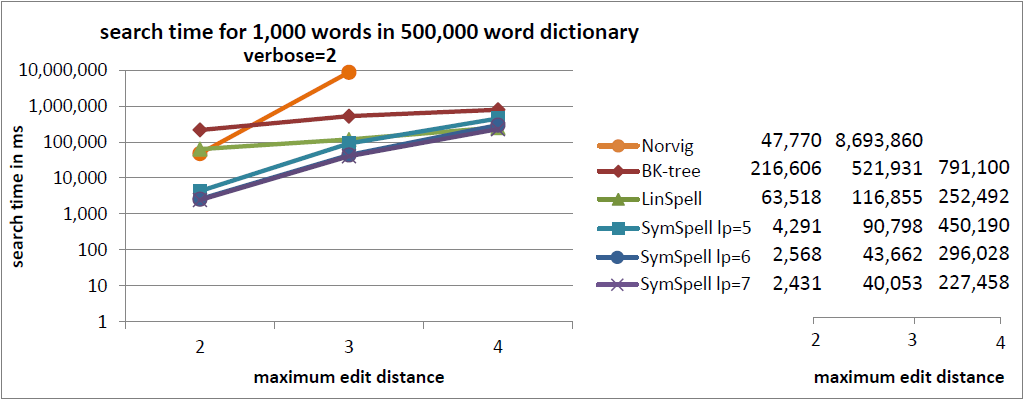
注釈：500,000単語収録の辞書内における1,000単語の検索時間
冗長＝2
X:最大編集距離
Y:検索時間/ms

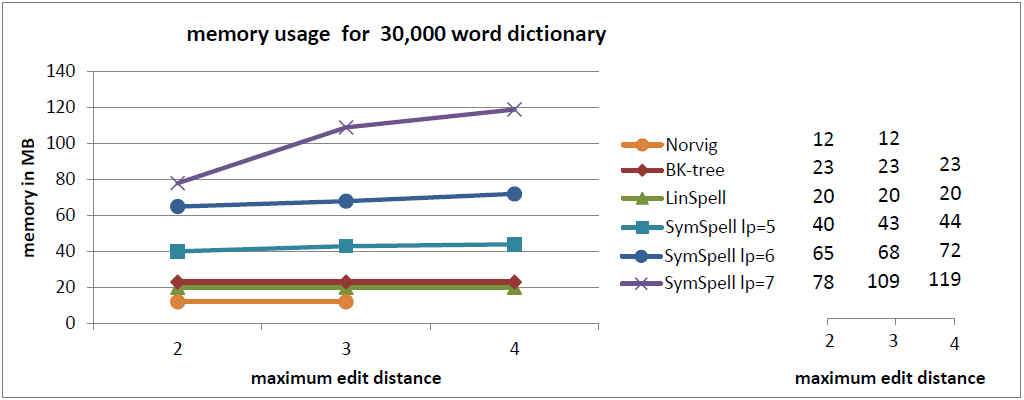
注釈：30,000単語収録の辞書内におけるにおけるメモリの使用
X:最大編集距離
Y:メモリ/MB

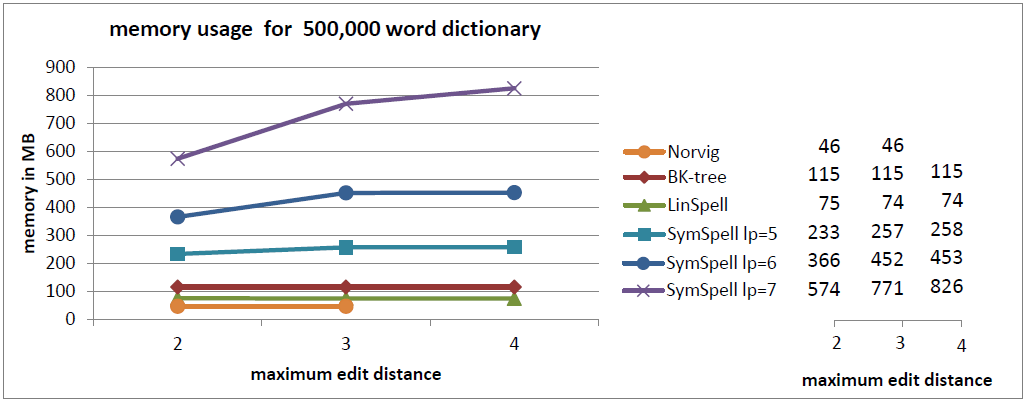
注釈：500,000単語収録の辞書内におけるにおけるメモリの使用
X:最大編集距離
Y:メモリ/MB

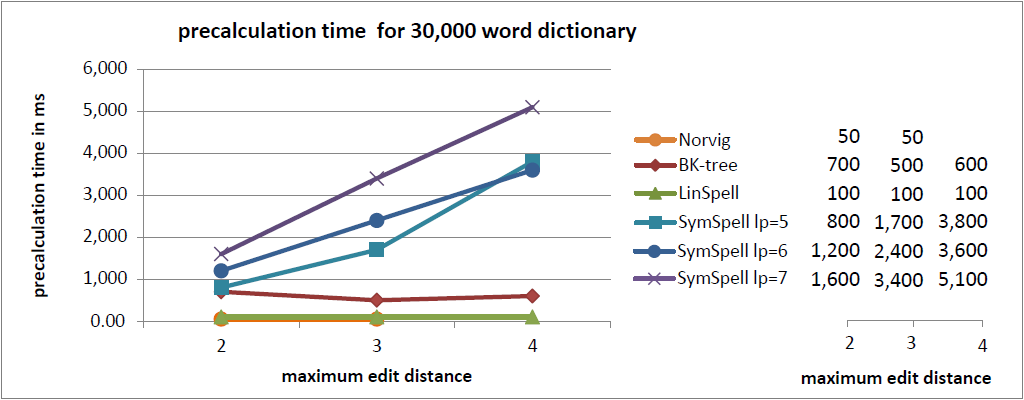
注釈：30,000単語収録の辞書内における事前計算時間
X:最大編集距離
Y:事前計算時間/ms

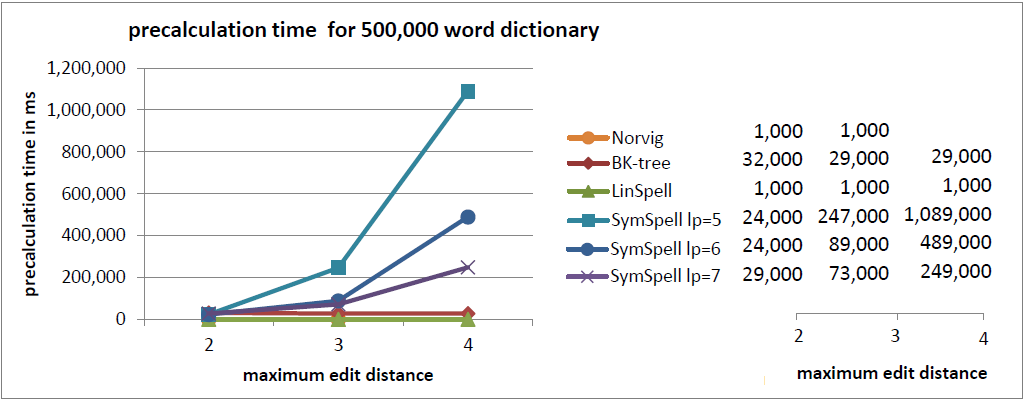
注釈：500,000単語収録の辞書内における事前計算時間
X:最大編集距離
Y:事前計算時間/ms

最新のベンチマークでは、 ランダムな編集 （0…最大編集距離）で単語を比較しました。この比較により、 平均検索時間 を把握することができました。

以前のベンチマーク では、 固定編集距離 （＝最大編集距離）の単語を比較していました。この比較により、 最大検索時間 を把握することができました。 平均は、ユーザ経験の測定としては誤解を招く場合があります 。編集距離＝3では、Norvigのアルゴリズムに比べて SymSpellは100万倍の速度でした。

まとめ

このベンチマークでは、BK木やNorvigのアルゴリズムが広く使われている背景には、ただ単に、歴史的な理由や教科書やフォーラムで長い間取り上げられていたという習慣的なもの以外には、論理的な理由は一切確認できませんでした。従来のアルゴリズムの代替案としては、SymSpellとLinSpellという2つのアルゴリズムが挙げられます。どちらも、少なくとも今回のテストの範囲内では常に従来のものより優れた結果を出しています。

• 速度を重視する場合はSymSpellの使用をお勧めします。BK木に比べて100倍から1,000倍高速であり、Norvigのアルゴリズムに比べると10万倍から100万倍高速です。 SymSpellの検索時間は辞書のサイズと最大編集距離に応じて穏やかに増大するだけです。全てのテストケースにおいて、その他3つのアルゴリズムより優れたパフォーマンスで、100倍、1,000倍の速さとなる結果もよく見られました。この場合、 メモリの消費量が増大し、事前計算時間が長くなってしまいます。 事前計算時間の損失は、事前計算のデータがシリアライズやデシリアライズされる場合、プログラムやサーバが起動する際やプログラム開発の際に一度発生するだけです。
• メモリ消費量を重視する場合はLinSpellの使用をお勧めします。BK木に比べると、同じメモリ消費量で10倍は速くなります。 LinSpellの検索時間は辞書サイズに比例して増加しますが、最大編集距離には依存しません。メモリ消費量が更に増えることはなく、事前計算時間の損失もありません。
• BK木を使用する明らかな利点はありません。全てのテストケースにおいて、SymSpellのほうが速度の点で優れており、LinSpellのほうが速度とメモリの点で優れています。 編集距離＞2の場合、BK木はNorvigアルゴリズムより高速ですが、LinSpellやSymSpellに比べるとかなり低速です。BK木の性能は辞書サイズに大きく左右されますが、最大編集距離に対しては、穏やかに低下するだけです。
• 冗長＝2は注意して使用しましょう （最小編集距離の結果だけではなく、最大編集距離内の全ての結果を列挙します）。これは非常に低速で、検索の早期終了が阻害されてしまいます。

更新

ベンチマークの結果が疑わしい というEメールを頂きました。メールの内容は、このテスト結果はBK木とSymSpellの アルゴリズムの違い というより、選択したBK木について C#の実装がうまくいっていない ためではないかというものでした。私としては、 可能な限り高速になるようなC#によるBK木の実装 を選び、このような疑念の入る余地がないように細心の注意を払ったつもりでした。しかし、言われてみれば確かに、パフォーマンスに対して、アルゴリズムの影響度合いが高いのか、それとも実装方法の影響度合いが高いのかを判別するのは、難しい場合もあるのかもしれません。

そこで、いくつかの 客観的なデータ を追加したいと思います。辞書を 検索する間に行われるレーベンシュタイン距離の計算の平均的な回数 です。

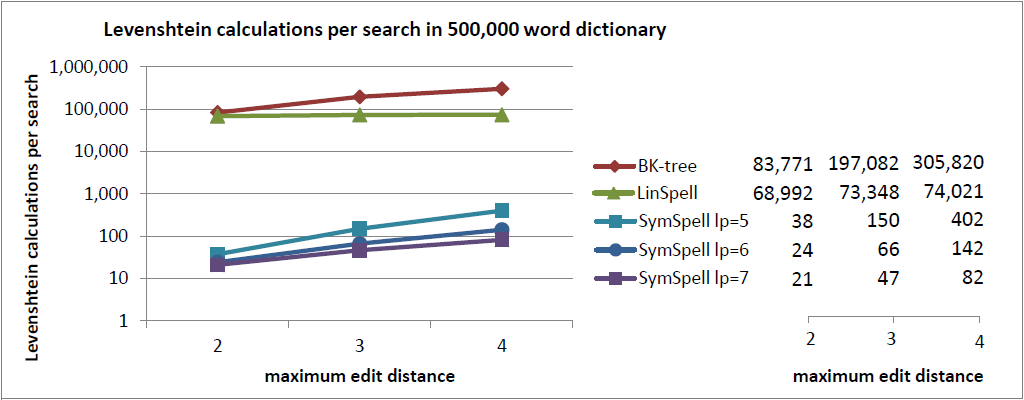
注釈：500,000単語収録の辞書内における1検索あたりのレーベンシュタイン距離の計算
X:最大編集距離
Y:1検索あたりのレーベンシュタイン距離の計算

レーベンシュタイン距離の計算は、BK木とSymSpellのどちらにおいても最も負荷のかかる検索コンポーネントです。 任意のサイズの辞書を検索する間に行われるレーベンシュタイン距離の計算の平均的な回数は、 その実装とは無関係に、純粋にアルゴリズムのパフォーマンスを表す非常に公正な指標となるはずです。

BK木では、（辞書に収録されている語の） 17％から61％の語彙 に対してレーベンシュタイン距離を計算する必要がありますが、SymSpellでは、必要な計算は、語彙の わずか0.016％から0.0042％に対してだけです。SymSpellが高速なのは、そのアルゴリズムの設計に由来する ものであり、その実装のせいではないのは、こうした理由によります。

話は変わりますが、私は、レーベンシュタイン距離の計算の必要回数をもっと減らしてフィルタリングする追加的ステップとして、 BK木における三角不等式の原理をSymSpellに統合する テストも実施しました。パフォーマンスは少ししか改善しませんでしたが、辞書を生成する際のレーベンシュタイン距離の計算に必要なメモリと事前計算のコストについては向上が見られました。