結局、やり出したら止まりません。私は以前、” I Wrote a Fast Hashtable（私が書いた高速なハッシュテーブル） “という記事と、それに次いで” I Wrote a Faster Hashtable（私が書いたより高速なハッシュテーブル） “という記事をブログにアップしましたが、今回ついに、最速のハッシュテーブルを書き上げました。これが意味するところは、ルックアップがどのハッシュテーブルよりも速いということです。それに加えて、挿入や削除も（最速とまではいかないまでも）非常に速く行えます。

秘訣は、探索回数の上限を設定したロビンフッドハッシュ法を使用することです。ある要素が、その理想的な位置からX数以上、離れた位置にある場合、テーブルを拡張することで、全ての要素が、その大きなテーブル内において、理想的な位置に近づくようにします。結果的に、このやり方は非常にうまくいきました。Xを相対的に小さくできるので、ハッシュテーブルルックアップの内部ループをいい具合に最適化できます。

前置きなしにこれをお試しになりたい場合、こちらの リンクでダウンロード 可能です。また、下にスクロールしていただければ、記事の後半に”ソースコードと使用法”というセクションがあります。より詳しい内容を知りたい方は、このまま読み進めてください。

ハッシュテーブルのタイプ

ハッシュテーブルには多くのバリエーションがあります。今回のハッシュテーブルに関しては、以下を選択しました。

• オープンアドレス法
• 線形探索法
• ロビンフッドハッシュ法
• 素数のスロット数（2のべき乗を使う選択肢も紹介します）
• 探索回数の上限を設定

これらの項目の最後のものは、ハッシュテーブル界に対する新たな貢献だと私は信じています。今回の速度向上における主な要因がこれです。しかしその前に、まずはその他の項目について話していきましょう。

オープンアドレス法とは、ハッシュテーブルの基本的なストレージが、連続配列であることを意味します。これは、全ての要素を別々のヒープアロケーションに格納するstd::unordered_mapとは、動く仕組みが異なります。

線形探索法とは、配列に要素を挿入しようとした時に、現在のスロットが既に埋まっている場合、隣のスロットを試すやり方です。隣のスロットが埋まっている場合、その隣のスロットを試します。このシンプルなアプローチには既知の問題がありますが、探索回数に上限を設けることで、それが解決されると私は信じています。

ロビンフッドハッシュ法とは、線形探索法を実行している時に、全ての要素をできる限り理想の位置に近づけて配置させようとするやり方です。この際、要素が挿入または削除される度にオブジェクトが移動されますが、その移動はリッチな要素から取り出してプアな要素に与える方法で行われます（ロビンフッドハッシュ法という名前の由来です）。”リッチ”な要素とは、理想的な挿入ポイントに近いスロットを受け取った要素のことで、”プア”な要素とは、理想的な挿入ポイントから離れた要素のことです。線形探索法で新しい要素を挿入する際、理想的な位置からどれくらい離れているかを数えます。理想的な位置が現在の要素より離れていれば、新しい要素を既存の要素と入れ替えて、既存の要素に新しい場所を見つけようとします。

素数のスロット数とは、基本配列が素数のサイズであることを意味しており、例えば、それが大きくなる場合、5スロットから11スロット、23スロットから47スロットといった具合に拡張します。挿入ポイントを見つけるには、単に剰余演算子を使用して要素のハッシュ値をスロットに割り当てればいいだけです。配列のサイズを決めるその他の一般的な選択肢としては、2のべき乗を使うことが考えられます。このブログの記事の後半では、私がデフォルトで素数を選んだ理由と、どの状況でどちらを使うべきかについて詳しく説明するつもりです。

探索回数の上限

基本的なことは抜きにして、早速、私の新しい貢献、つまりテーブルがスロットを検索する回数の制限（それを超えると、テーブルはスロットの検索を諦めて基本配列を拡張する）について話しましょう。

私は最初、この回数を非常に低い数字、例えば4に設定しようと考えました。つまり挿入時に、理想的なスロットを試してみて、それがダメなら隣のスロットへ、またダメならその隣のスロットへ、そしてその次も埋まっていてダメだった場合は、テーブルを拡張して再挿入を試みるという流れです。これは、テーブルが小さい時は非常に好感触でしたが、大きいテーブルにランダムな値を挿入すると全然ダメで大抵は4回の探索限度に達し、ほとんどが空にもかかわらずテーブルを大きくする羽目になりました。

その代わりに見つけた上限の回数が、log2（n）です（nはテーブルのスロット数）。これにより、再割り当てまでに、テーブルが大体3分の2は埋まるようになりました。なお、これはランダムな値を挿入した時です。連続した値を挿入した場合は、再割り当てが必要になる前にテーブルは完全に埋まります。

さて、テーブルを大体3分の2までは埋めることができるようになりましたが、時折60％までしか埋まっていないのに再割り当てすることもありますし、頻度は少ないですが、55％の時もあります。そこで、テーブルのmax_load_factorを0.5に設定しました。これにより、探索回数が上限に達していなくても、テーブルが半分埋まった状態でテーブルは拡張するようになります。こうした理由は、自分が決めたしきい値でのみ再割り当てが行われるような確実なテーブルにしたかったからです。1000個の要素を挿入した後で、いくつかを削除してそれと同数の要素を再び挿入しなおしても、これならテーブルが再割り当てされないことはほぼ確信できます。その確実性を数値で表すことはできませんが、多種多様なサイズの数千のテーブルを構築し、それらにランダムな整数を埋め込む簡単なテストを実行しました。全体的に、テーブルに何億もの整数を挿入しましたが、0.5未満の占有率で再割り当てしたのは1度だけです（その時はテーブルの占有率が48％と、わずかに早い段階での拡張でした）。このことから、想定外の再割り当ては非常に希だと言うことができると思います。

とは言うものの、テーブルの拡張を制御する必要がないならば、max_load_factorを高めに設定しても構いません。0.9に設定しても完全に安全です。ロビンフッドハッシュ法に探索回数の上限設定を組み合わせることで、全ての操作が高速になります。ただし、1.0には設定しないでください。この場合、挿入時にトラブルが起こりかねません。場合によっては、最後の要素を挿入する時にテーブル内の全ての要素を移動しなければならないケースが発生します（例えば、最後のスロットを残して全ての要素が所定のスロットに収まっているとします。ここで、最後に入れる要素が第1スロットに入りたいとしましょう。しかし第1スロットは既に埋まっています。仕方なくその要素は第2スロットに入ることになりますが、そうすると、第2スロットに入っていた元の要素を押しのける形になってしまい、それが第3、第4と続き、最後のスロットが埋まるまで延々と繰り返されることになってしまうのです。この場合のテーブルは、第1スロットを除く全ての要素が理想のスロットから1スロット分離れただけなので、ルックアップは依然として高速ですが、最後の挿入には時間がかかります）。空のスロットをいくつか残しておくことで、新たに要素が挿入されても、押しのけられる要素が空のスロットを見つけるまでの数スロット分で移動が済むようになります。

max_load_factorを低く設定した場合、探索回数が上限に達することはなさそうなのに、なぜ限界を設定するのでしょうか。それは、そうすることで良好な最適化が可能になるからです。例えば、テーブルを再ハッシュして1000スロットにするとしましょう。私のハッシュテーブルは、最も近い素数である1009スロットに拡張します。そのlog2は10なので、探索回数の上限を10に設定します。そして、ここで1009スロットの配列を割り当てるのではなく、1019スロットを割り当てます。これはちょっとしたトリックで、その他のハッシュ操作は依然として1009スロットが前提です。こうすることで、もし2つの要素がインデックス1008にハッシュした場合でも、単に最後までに行き、インデックス1009に挿入することが可能となります。探索回数が、その上限によりインデックス1018を超えないため、境界チェックをする必要はありません。仮に最後のスロットに入りたい要素が11個ある場合は、テーブルが拡張し、それらの要素は別のスロットにハッシュされます。境界チェックがなく、内部ループはごく小さなものです。find関数は次のようになります。

iterator find(const FindKey & key)
{
    size_t index = hash_policy.index_for_hash(hash_object(key));
    EntryPointer it = entries + index;
    for (int8_t distance = 0;; ++distance, ++it)
    {
        if (it->distance_from_desired < distance)
            return end();
        else if (compares_equal(key, it->value))
            return { it };
    }
}

基本的には線形探索で、非常に美しいアセンブリとなります。これは、2つの観点から単純な線形探索より優れています。1つ目は境界チェックがないことです。空のスロットのdistance_from_desired値は-1なので、空の場合は、別の要素を見つける場合と同じです。2つ目に、これはループにおけるlog2（n）回の反復の大部分に対して有効です。通常、ハッシュテーブルの検索で最悪のケースはO（n）で、私にとってはO（log n）です。特に線形探索は要素を束ねる傾向があり最悪のケースに遭遇しやすいため、これは本当に大きな違いとなります。

この場合のメモリオーバーヘッドは要素ごとに1バイトです。distance_from_desiredはint8_tに格納します。というわけで、その1バイトは挿入する型のアラインメントにパディングされます。従って、intを挿入すると、その1バイトは3バイトのパディングを取得するので、1要素あたりのオーバーヘッドは4バイトです。ポインタを挿入すると、パディングは7バイトとなるため、1要素あたりのオーバーヘッドは8バイトとなります。これを解決するためにメモリのレイアウトを変更することを考えましたが、そうするとそれぞれのルックアップに対して1つのキャッシュミスではなく、2つのキャッシュミスを心配しなくてはならなくなるでしょう。そのため、メモリオーバヘッドは1要素あたり1バイト＋パディングとします。それから、max_load_factorが0.5（デフォルト）の場合、テーブルの占有率は25％から50％の間を超えないので、オーバーヘッドが増えます（ただし、繰り返しになりますが、メモリを節約するためにmax_load_factorを0.9に増やしても安全です。その場合、速度はわずかに低下します）。

ルックアップのパフォーマンス

実は、ハッシュテーブルの測定は容易ではありません。少なくとも、以下のケースについて測定が必要です。

1. テーブル内の要素のルックアップ
2. テーブル内にない要素のルックアップ
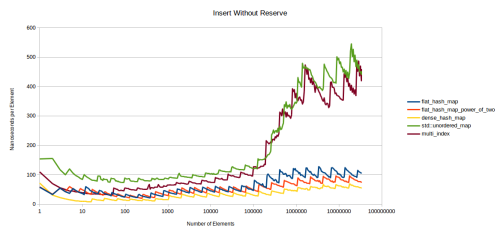
3. ランダムな数値群の挿入
4. reserve()を呼び出した後に、ランダムな数値群を挿入
5. 要素の削除

上記の各ケースを、異なるキーと異なる値のサイズで実行する必要があります。私はintまたはstringをキーとして使用します。その際、値のサイズは4、32、1024のタイプを用います。stringキーを使うと、ほとんど、ハッシュ関数のオーバーヘッドと比較演算子を測定することになりますが、このオーバーヘッドは全てのハッシュテーブルについて同様ですので、intキーを使います。

ルックアップが成功するケースと失敗するケースの両方をテストする理由は、テーブルによっては、この2つのケースの間でパフォーマンスに大きな違いがあるからです。例を挙げると、0から500000までの全ての数をgoogle::dense_hash_map（数字はランダムではありません）に挿入し、続いて、失敗するルックアップを実行した際に、最悪のケースに当たりました。このハッシュテーブルは突然、通常の500倍も遅くなったのです。これは、テーブルのサイズを決める際に2のべき乗を使用した場合のエッジケースです。2のべき乗を採用するべき場合と、素数を採用するべき場合についてもう少し詳しく以下にご紹介します。先ほどの例から考えると、本当は、ランダムな数字と連続的な数字を使用して各測定を行うべきところでしょう。ただしそれでは、グラフの数が多くなり過ぎます。ですから、特定のパターンによって引き起こされた悪いケースを回避するような、ランダムな数を使ってテストするだけにしておきましょう。

この最初のグラフは、テーブル内の要素をルックアップしています。

かなり込み入ったグラフなので、少し時間をかけて見ていきましょう。flat_hash_mapは、本稿でご紹介している新しいハッシュテーブルです。flat_hash_map_power_of_twoは同じ様なハッシュテーブルですが、配列サイズに素数ではなく2のべき乗を使用しています。ご覧のように非常に高速ですが、後でその理由を説明します。dense_hash_mapは、google::dense_hash_mapで、私が知る限り最も高速なハッシュテーブルです。sherwood_mapは私の投稿記事”I Wrote a Faster Hashtable”で紹介した古いハッシュテーブルです。これはどうしようもないほど低速です。std::unordered_mapとboost::unordered_mapは読んで字のごとくです。multi_indexはboost::multi_indexのことです。

このグラフについて少しお話したいと思います。Y軸は1つの要素をルックアップするのに要するナノ秒です。googleベンチマークを使って、0.5秒の間にtable.find()の呼び出しを繰り返し行い、何回呼び出せるのかをカウントします。この繰り返し全体にかかった時間をループカウントで割ることで、ナノ秒を取得します。検索対象のキーは全てテーブル内にあることが保証されています。X軸にはログスケールを取ることにします。これは、パフォーマンスがログスケールで変化する傾向があるからです。X軸にログスケールを取れば、異なるスケールでパフォーマンスを確認できます。小規模なテーブルについて知りたければ、グラフの左側部分を見ればよいでしょう。

まず気が付くのは、どのグラフもギザギザであることです。これは、ハッシュテーブルは全て、現在の占有率によって異なるパフォーマンスを見せるからです。つまり、テーブルがどれくらい埋まっているかに依存するということです。テーブルが25％埋まっている場合のルックアップは、50％埋まっている場合よりも速くなります。テーブル内がいっぱいであれば、より多くのハッシュの衝突が起きるからです。このコストがある程度まで上がると、テーブルは、一定のラインを超えて空きが無くなったので再割り当てするべきであると決定します。そうすると、ルックアップが再び高速になります。

もし、各テーブルの占有率をプロットすれば明らかになるでしょう。更に、グラフの一番下に位置するテーブルのmax_load_factorは0.5であり、一番上のテーブルのmax_load_factorは1.0であることも分かると思います。ここで、すぐに”他のテーブルも、max_load_factorを0.5にすれば高速になるのではないか”という疑問が生じます。少しは速くなる、というのがその答えです。しかし、ずっと後でご紹介する別のグラフを使って、より十分な形で回答したいと思います（しかし、上記のグラフを見ただけでも、上の方に位置するグラフの、占有率が0.5をちょうど超えた時点でちょうどテーブルが再割り当てされた時点でも、下の方に位置するグラフの最も高いポイントよりはるかに上にあることが分かります。下の方のグラフの占有率は0.5のちょっと手前なので、再割り当ての直前です）。

他にも、どのグラフも左側の部分は基本的に平坦であるということに気付きます。これは、テーブルがキャッシュに完全に収まるからです。データがL3キャッシュに収まらないポイントに達した場合にのみ、グラフは別々に分岐します。これは大きな問題だと思います。現実的なのは、左側の数値よりも右側の数値です。検索対象の要素が既にキャッシュ内にある場合だけ、左側の数値が得られるでしょう。

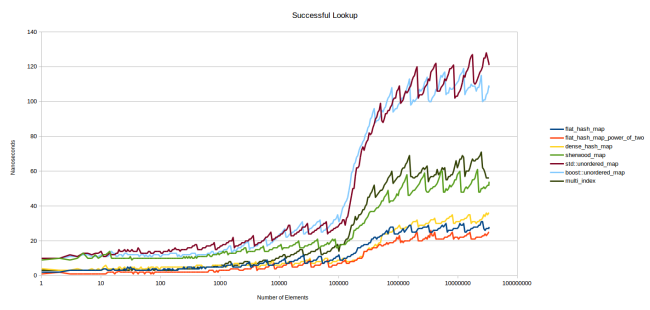
こうしたことから、もし対象がキャッシュ内にない場合のテーブルの速度を測定してみようと思いました。L3キャッシュに完全に収まりきらないくらい十分な数のテーブルを作成し、検索する各要素について異なるテーブルを使用します。ここでは8バイトのサイズの要素を32個持つテーブルを測定しようと思います。L3キャッシュは6メビバイトなので、L3キャッシュ内に約25000のテーブルをキャッシュに入れられます。テーブルがキャッシュ内に入りきらないことを確実にするために、この3倍、つまり75000のテーブルを作成しました。そして、異なるテーブルで各検索を行います。その結果は以下のグラフのようになります。

まず、いくつかの折れ線を削除します。これらの折れ線からはあまり追加情報が得られないからです。boost::unordered_mapは、通常std::unordered_mapと同じ速度であり（少し速くなる場合もありますが、いずれにせよ他のどのテーブルよりもグラフの上の方に位置します）、私の古くて低速なハッシュテーブルsherwood_mapについては、気にする人などいないでしょう。これらを削除した結果、重要な折れ線のみ残りました。通常ノードベースのコンテナであるstd::unordered_map、実に速いノードベースのコンテナであるboost::multi_index（std::unordered_mapはこのくらい速いと思っています）、高速なオープンアドレス法のコンテナであるgoogle::dense_hash_map、素数を使用したバージョンと、2のべき乗を使用したバージョンの私の新しいコンテナです。

さて、キャッシュミスをするように強いたこの新しいベンチマークでは、早い段階で大きな差が見られます。前回のグラフでは終盤に見られたパターンが、このグラフではかなり早くから現れているのが分かります。テーブル内の要素が10の状態で開始したところ、パフォーマンスの点で明らかに優れているものがあります。これは実際、非常に顕著なパフォーマンスです。全てのハッシュテーブルが、異なる規模で、一貫したパフォーマンスを維持しています。

ルックアップが失敗したグラフも見てみましょう。アイテムを検索した結果、テーブル内に無かった場合です。

ルックアップが失敗した場合、グラフはより一層ギザギザになっています。ここでは占有率が大きな問題になります。テーブルが埋まっているほど、アイテムがテーブル内にないと結論を出すまでに多くの要素を探さなければなりません。でもここで、私の作った新しいテーブルの処理の成果には満足しています。探索回数を限定したことが効果を上げています。他のどのデーブルよりも、一貫したパフォーマンスを実現しています。

私の新しいテーブルが、大きな前進を遂げていることがグラフから分かります。2のべき乗を用いた赤色の系列は、dense_hash_mapと同じように設定された私のテーブルです。max_load_factor0.5で、テーブルサイズの決定に2のべき乗を用いて、下位ビットを見ることによりハッシュがスロットにマップされるようにします。唯一の大きな違いは、私のテーブルはテーブルのスロット当たりの余剰ストレージ（さらにパディング）に1バイトを使うという点です。私のテーブルはdense_hash_mapに比べて少し余計にメモリを使用します。

驚くべきことに、私のテーブルは、テーブルのサイズ決定に素数を使う場合も、dense_hash_mapと同じくらい高速です。これについて少しお話しましょう。