「数値最適化」は機械学習における中心的手法の1つです。多くの問題では、最適解を直接突き止めることは難しいものですが、ある解がどれほど適しているかを測定する損失関数を設定し、解を見つけるためにその関数のパラメータを最小化することは比較的容易です。

かつてJavaScriptを初めて学ぼうとしていた時 、結果的に数値最適化ルーチンを多数書きました。そのコードを特に使うこともなく置いていたので、それらのアルゴリズムの動作をインタラクティブな形で可視化したら面白いのではないかと考えました。

本記事の良い点は、コードが全てブラウザで実行できることです。つまり、アルゴリズムの動作をより把握するために、各アルゴリズムのハイパーパラメータをインタラクティブにセットしたり、初期位置を変更したり、どの関数が呼び出されるかを変更したりすることができるのです。
(編注：本記事ではスクリーンショットのみ公開しております。上記機能については 元記事 で動作をお試しください。)

本記事のコードは全て、 GitHub にアップしていますので、関心のある方はご覧ください。可視化例の全てはもちろん、最小化関数も含まれています。

ネルダーミード法

少しの間、微積分や基礎的な代数学さえも思い出せない振りをしてください。ある関数を与えられて、その最小値を見つけるよう指示されたとしましょう。

1つ簡単に試せるのは、比較的近い2点を抽出して、最大値から離すステップを単に繰り返していくことでしょう。

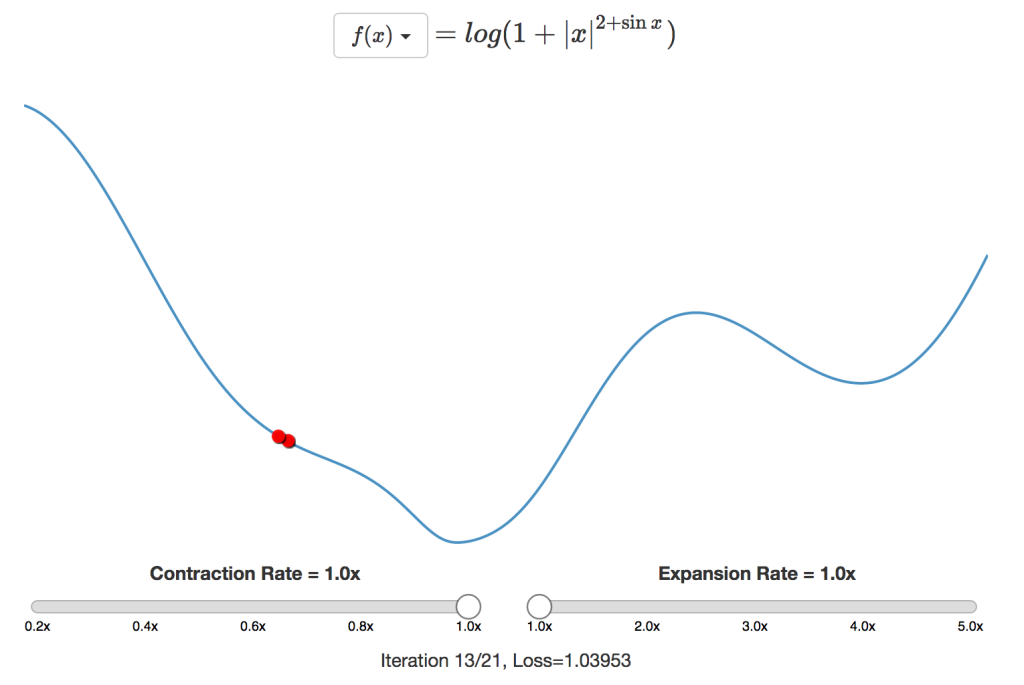
このアプローチの明らかな問題点は、固定のステップサイズを使っているということです。それでは真の最小値にそのステップサイズでしか近づけないので、収束しません。また、ステップサイズを大きくすべきだということが明らかな場合、最小値に少しずつ近づくのでは時間がかかりすぎます。

こうした問題を克服するため、 ネルダーミード 法では、新しい点の損失に基づいてステップサイズを動的に調整します。新しい点の値が以前の値より良ければ、最小値により早く達するようステップサイズを拡張します。同様に、新しい点の値が前の値より悪ければ、最小値周辺に収束するようステップ幅を収縮します。

通常の設定では、収縮時はステップサイズを半分に、拡張時はステップサイズを倍にします。上に挙げた1次元の例では、最小値の範囲が定まるまではギャロッピング探索のようにサイズを倍にし、収縮に転じたら二分探索を実行します。

この手法は高次元の例にも容易に適用できます。必要なことは次元数より1つ多い数の点を用意することと、ステップダウンするために残りの点の最も悪い点を反映させることだけです。こちらの 等高線図 で、2次元での動作を見てみましょう。

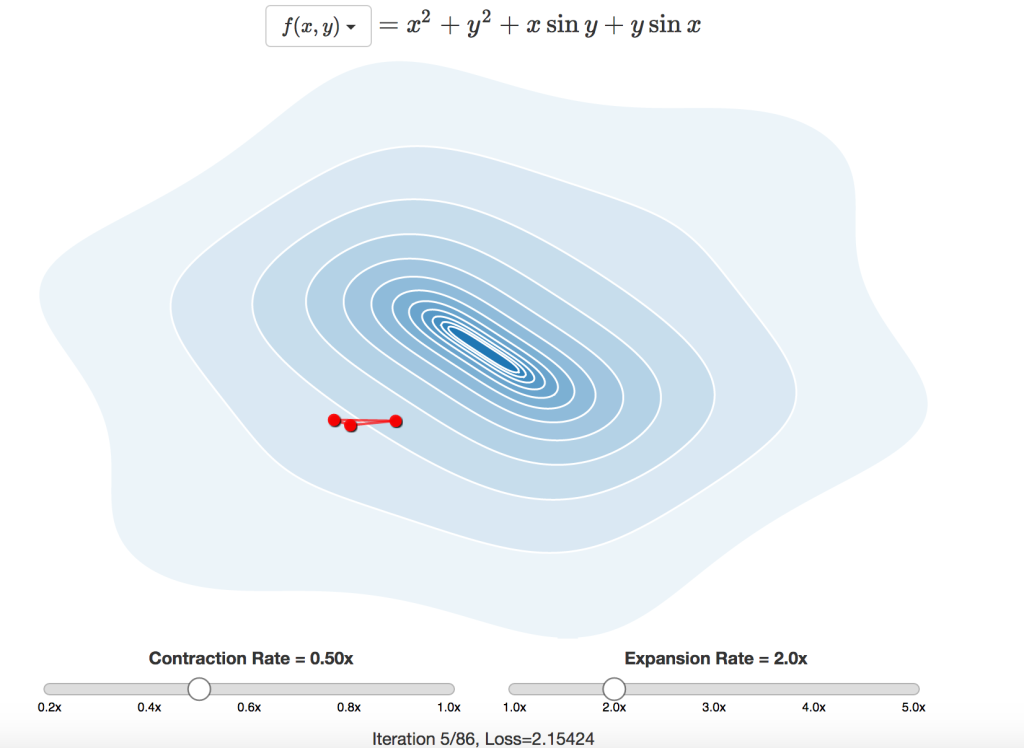
グラフのどこかをクリックすると、新しい初期位置からやり直します。その位置に三角形を生成し、設定に応じて必要であれば拡張または収縮を行いながら、最小点に向かって反転を繰り返します。
(編注：上記機能については 元記事 で動作をお試しください。)

この方法は非常に単純ですが、実際のところ低次元関数では結構うまく動作します。 f ( x ) = | ⌊ x ⌋ − 50 | のように微分不可能な関数さえも最小化することが可能です。以降でご説明する他の方法ではいずれも、微分不可能な関数を最小化することはできません。

こういった直接探索法に共通する最大の欠点は、関数の次元が高くなるにつれて動作が遅くなるということです。上述したような1次元と2次元の例ではネルダーミード法はうまく動作するのですが、機械学習モデルのパラメータは何十億個まではいかなくても何百万個に増加する可能性はあります。しかしネルダーミード法は、パラメータが十数個程度の単純な問題でもうまくいきません。

進行方向の求め方も問題の1つです。2次元空間ではそれほど難しくないのですが、次元数が増えるにつれて加速度的に難しくなるのです。

勾配降下法

進行方向として1つ考えられるのは、現在の点における勾配 ∇ F ( X n ) を求め、そのに最小値に向かって勾配をステップダウンすることです。勾配は損失関数を記号微分するか、 Torch や TensorFlow と同様に 自動微分 を使うことで計算できます。つまり、固定のステップサイズ α を使って、現在の点 X n を下記で更新するのです。

X n + 1 = X n − α ∇ F ( X n )

X(n + 1) = X(n) − α∇F(X_(n))

これによって勾配降下の経路を選択することになります。大まかにいえば、局所的最小値の1つに向かって坂を転がり落ちるボールのような感じです。

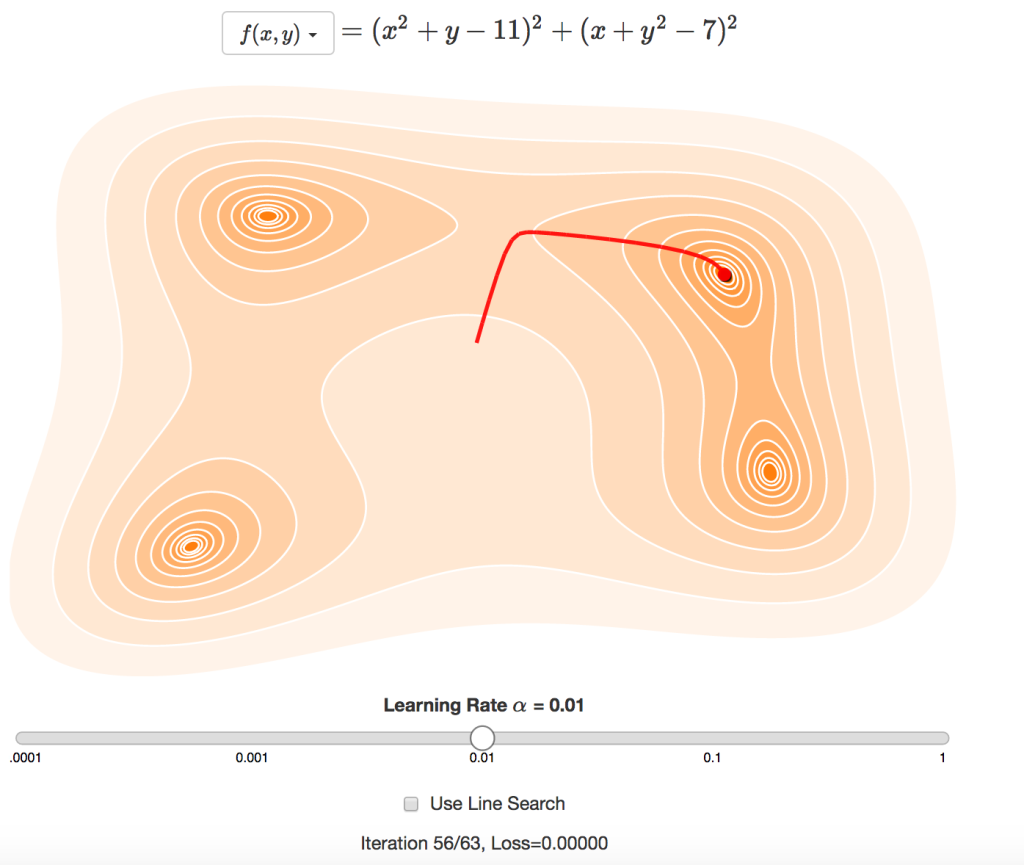
この方法では学習係数の設定が問題となります。学習係数を低くしすぎると、なかなか解にたどり着かず、解に向かう小さなステップを何回も繰り返します。学習係数を高くしすぎると、収束することなく、最小値周辺を激しく変動します。さらに悪いことに、最適な学習係数は関数によって異なるため、これという適切な初期値がないのです。

直線探索 を使うと、反復の度に学習係数を修正することができます。これは、最小値を通過しないよう損失を常に減らすと共に、小さなステップを繰り返しすぎないよう勾配を平坦化するためです。上図で直線探索を有効にすると、反復の度に余分なサンプル点が必要になるかもしれないという欠点はあるものの、反復回数が減少します。
(編注：上記機能については 元記事 で動作をお試しください。)

直線探索を使う時でも、勾配降下法はRosenbrock関数のような関数を扱うにはやはり苦労します。問題点は、最適な進行方向が勾配に沿わない場合があるので、関数の曲率も考慮する必要があるということです。

共役勾配法

共役勾配法では、より良い新たな探索方向を見つけるため、現在の勾配に前回の探索方向を含めて最小化を行い、関数の曲率を推定します。

Jonathan Shewchukは、「 An Introduction to the Conjugate Gradient Method Without the Agonizing Pain 」（苦しまない共役勾配法入門）と題した素晴らしい論文を書き、共役勾配法の仕組みを詳細に解説しています。唯一問題なのは、この論文が本記事全体よりはるかに長いということで、42ページ目からやっと非線形共役勾配法の説明が始まっています（彼が学んだ際の”苦しさ”を思うとゾッとします）。

共役勾配法の背後にある理論は少し複雑ですが、数学的にはかなりシンプルです。初期探索方向 S 0 は勾配降下法の場合と同じです。それ以降の探索方向 S n は下記で計算します。

β = ∇ X T n ( ∇ X n − ∇ X n − 1 ) ∇ X T n − 1 ∇ X n − 1

$$ \beta = \frac{\nabla Xn^T(\nabla Xn - \nabla X_{n-1}) }{\nabla X^T_{n-1} \nabla X_{n-1}} $$

S n = ∇ X n + β S n − 1

S(n) = ∇X(n) + β**S_(n − 1)

現在位置 X n は、この探索方向と、直線探索で計算されるステップサイズ α を使って更新されます。

X n + 1 = X n + α S n

X(n + 1) = X(n) + α**S_(n)

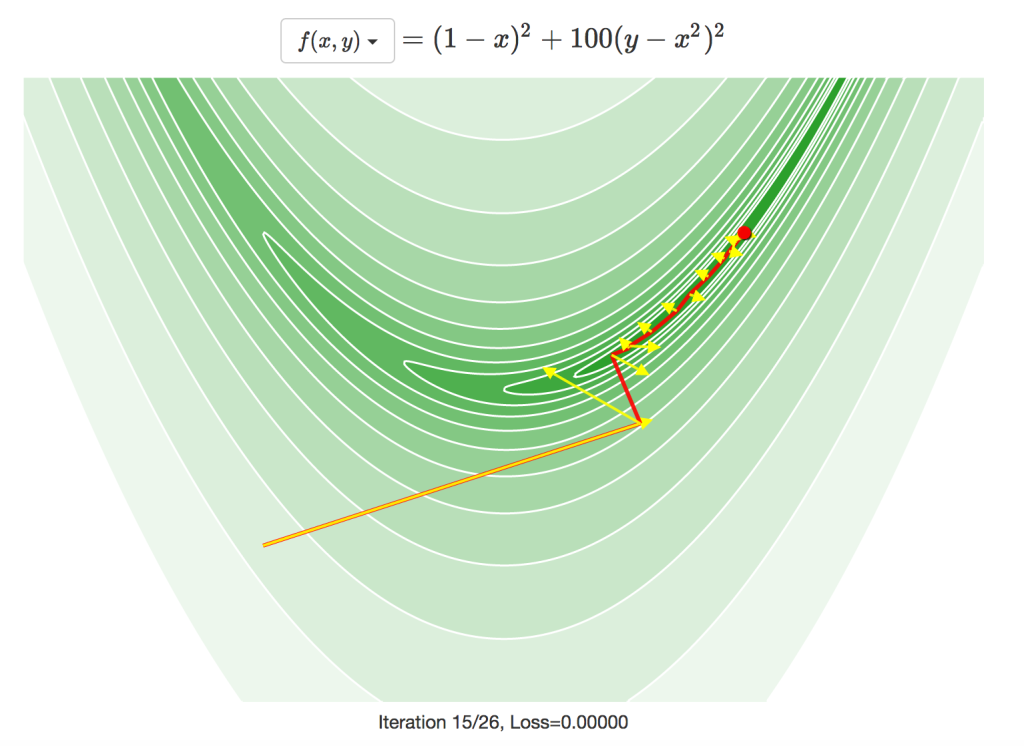
共役勾配法の経路は下図で確認できます。実際に進んだ方向は赤色で、各反復での勾配は黄色の矢印で示されます。中には、使われている探索方向が勾配に対してほぼ90度の場合もあり、下記の関数では勾配降下法を使うと大きな問題があることが分かります。

別の例

ここまでの例で登場したのは1次元関数か2次元関数のみで、最適化対象としてはあまり面白くありません。また、実際のデータも使ってきませんでしたが、大抵の機械学習の問題では実データを扱うのが普通です。そこで最後の例として、こうしたアルゴリズムが 多次元尺度構成法 の問題でどう動作するかを見ると面白そうです。

ここでの課題は、点間の距離行列を必要な距離に最も近い各点の座標に変換することです。それを実行する方法の1つは、以下のような関数を最小化することです。

l o s s = ∑ i ∑ j ( ( X i − X j ) T ( X i − X j ) − D 2 i j ) 2

los**s = ∑(i)∑(j)((X(i) − X(j))^(T)(X(i) − X(j)) − D_(i**j)²)²

X i は最小化の対象とする各点の座標、 D i j は各点間の望ましい距離です。

使用しているデータは北米の主要都市間の距離で、このデータを使って各都市のマップを作成することが目標です。20都市間の距離を渡すということは、40個のパラメータで最小化する関数が必要になるということです。

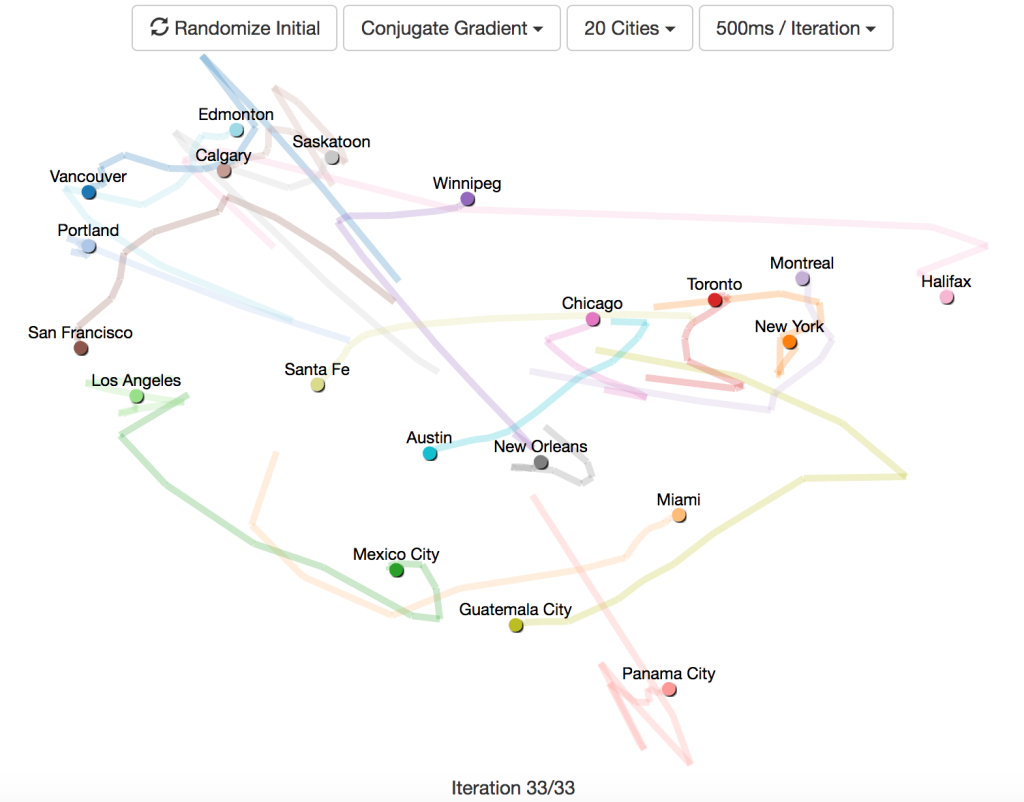
この可視化例は以下のことをかなり明確に示しています。

• ネルダーミード法は、10都市を超えると全くうまくいかない。10都市以内の場合でも、他の方法に比べて苦労する。
• 勾配降下法は、学習係数が適切であればうまく動作するが、最適な学習係数は都市の数によって異なる。学習係数を大きくしすぎると収束せず、小さくしすぎると長い時間がかかる。
• 勾配降下法で直線探索を使うと経路がジグザグとなり、共役勾配法ではそれが滑らかになる。

参考資料

ここまで読み通した方は恐らく、本記事が言語を学ぶための誤った試みの一部で、いくつかのJavaScriptコードを使いこなすための言い訳に過ぎないことにお気付きでしょう。今回ご紹介したことは全て既知の情報で、その多くについては、この記事よりはるかにうまく説明している資料があります。

NocedalとWrightが執筆した 数値最適化に関する優れた書籍 は、本記事の大部分で参考にしました。これは素晴らしい参考資料ですが、同書で扱われていないいくつかの手法をお伝えしておきたかったのです。

Sebastian Ruderの記事は、 勾配降下法 （翻訳記事「 勾配降下法の最適化アルゴリズムを概観する 」）を見事に概観しています。特に、ディープニューラルネットワークの訓練で使われるような大規模でまばらなモデルで確率的勾配降下法を用いるケースについて、詳しく論じています。

導関数を使わない優れた最適化手法の1つにベイズ最適化があります。Eric Brochu、Mike Vlad Cora、Nando de Freitasは、 ベイズ最適化に関する素晴らしい概論 を執筆しました。ベイズ最適化の応用例として1つ興味深いのはハイパーパラメータの調整で、そのためにベイズ最適化をサービスとして提供している SigOpt という企業さえ存在します。