前編はこちら： 深層強化学習：ピクセルから『ポン』 – 前編

起こっていないこと

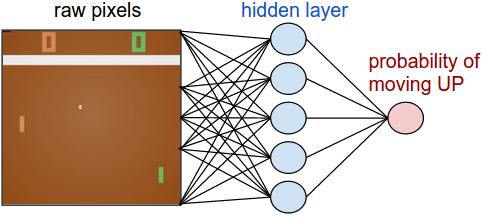
さて、方策勾配を使って生のピクセルから『ポン』をプレイする方法を学びましたが、ご理解いただけましたね。この手法は推測してチェックするという手間のかかるやり方で、”推測”は最新の方策からロールアウトをサンプリングすることを意味し、”チェック”は良い結果を導くアクションを促すこと意味します。大枠では、これは強化学習の問題への最先端のアプローチです。このような振る舞いを学習できるということは感動的です。しかしあなたが直感的にアルゴリズムを理解していて、どのように機能するか知っているとしたら、少しがっかりしてしまうのではないでしょうか。具体的に、機能しないのはどういうところでしょうか。

これと比較して、人間は『ポン』のプレイ方法をどのように学習するでしょうか。おそらくあなたはゲームを見せ、次のように言います。「パドルをコントロールして、上下に動かして。AIで制御された対戦相手からのボールを打ち返して」。これでもう大丈夫です。違いに気付きましたか。

• 実際の状況では、タスクについて通常（上記の説明のような）ある一定の手法で伝達します。しかし標準的なRL問題では、環境とのやりとりの中で任意の報酬関数を発見し、想定します。もし報酬関数についてまったく知らずに人間が『ポン』ゲームに取り組んだ場合（報酬関数が静的で無作為な関数だった場合は特に）、学習に大いに苦労するでしょう。しかし、AIが方策勾配で学習する場合は特に変わりなく、むしろうまく実行する傾向にあると言えます。同じように、フレームを見て無作為にピクセルの順序を変更すれば人間は失敗してしまいそうですが、方策勾配法は（ここでの例のようにネットワークが完全に接続されていた場合）その違いに気付きもしないでしょう。
• 人間は大量の事前知識を持っています。例えば物理についての直感的理解（ボールははずむ、瞬間移動はしない、突然止まったりもしない、一定の速度を保つ、など）や、直観的な心理学（AIの対戦相手は「勝ちたい」と思っている、ボールの方向に動くなど明確な戦略に従う）です。パドルを「コントロール」している状態も理解していますし、動きがUP/DOWNのキーコマンドに対応しているということも知っています。一方、アルゴリズムはゼロからのスタートです。（機能するので）素晴らしいのと同時に、（機能しない時の具体的な理由が分からないため）がっかりする面もあります。
• 方策勾配は 力づく のソリューションです。正しいアクションが徐々に発見され、方策に習得されていきます。人間は豊かで抽象的なモデルを構築し、その中で進め方を考えます。『ポン』では、対戦相手がかなり遅いと推論できるので、高い垂直速度でボールを返す戦略が良さそうです。対戦相手が打ち返せないからです。しかし、反応の早いマッスルメモリーの方策のような優れた方法を徐々に”習得させる”べきだ、とも感じるでしょう。例えばあなたが何か新しい運動に関するタスク（例えばマニュアル車の運転）を学んでいると仮定してみましょう。最初は大いに頭を使うでしょうが、やがて無意識に何も考えなくてもできるようになるでしょう。
• 方策勾配は実際にポジティブな報酬を経験する必要があり、その経験はかなり頻繁でなくてはいけません。方策のパラメータを、より高い報酬を与える反復動作に徐々にシフトしていくためです。人間には抽象モデルがあるので、実際に成功と失敗のトランジションを経験しなくても、報酬を与えられるのはどういうことか、分かります。車を壁にぶつけないようにするために、実際に何百回も衝突させてみる必要はありません。

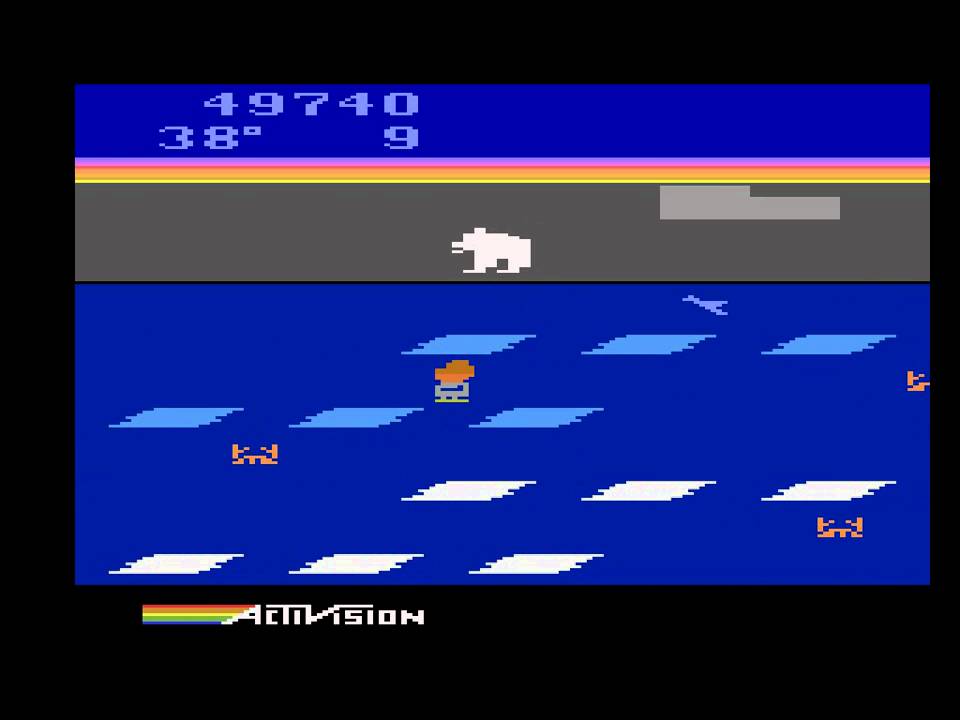
上： 『モンテスマの復讐！』：RLアルゴリズムには困難なゲームです。プレイヤーは飛び降りたりよじ登ったりして、鍵を取得し、扉を開けなくてはなりません。人間は、鍵を入手するのが有効だと理解します。コンピュータでは何十億もの無作為の動きをサンプリングしても、99％は死んだり、モンスターに殺されたりします。言い換えると、報酬を得られる状態に”転がり込む”のが難しいのです。 下： 『Frostbite』と呼ばれる他の難しいゲームです。人間は、『Frostbite』では物が動かせて、触っていいものもあり、触ってはいけないものもあり、ゴールはイグルー（イヌイットの住居）を作ることだと理解しています。このゲームについての優れた分析と、人間とコンピュータのアプローチの違いについての考察を 『人のように学び考える機械を構築する』 という記事で読むことができます。

強調したいのは、逆に、方策勾配が簡単に人間を負かすことのできるゲームもたくさんあるということです。特に頻繁な報酬シグナルがあって、正確なプレイ、高速な反射、そしてあまり長期計画の必要でないものが理想的です。なぜならこの手法では短期間での報酬とアクションの相関関係に簡単に”気付く”ことができ、方策が細心の注意を払って実行するからです。これはすでに私たちの『ポン』エージェントでも起こっていることが示唆されています。ボールを待ち、端っこで捕らえるため急速にダッシュし、素早く高い垂直速度で打ちます。エージェントはこの戦略を繰り返して数ポイント連取しました。Deep Q Learningがこのような方法で人間の基本的なパフォーマンスを打ち破るATARI製ゲームはたくさんあります。例えば、『ピンボール』、『ブロックくずし』などがそうです。

結論として、これらのアルゴリズムが使う”トリック”を理解すれば、彼らの強みと弱みを推察することができます。とりわけ、いくら計画し高速学習しても、ゲームの抽象的かつ豊かな表現に関しては人間にはまったく及びません。いつかコンピュータがピクセルの配列を見て、鍵や扉に気付き、鍵を拾って扉に近づけばいいと考える日も来るかもしれませんが、今は、これにはまったくほど遠い段階です。そのレベルに到達していくことが活発な研究分野になっています。

ニューラルネットワークでの微分不可能な演算

もう1つ、ゲームには関係のない、方策勾配法の興味深い応用について言及したいと思います。微分不可能な演算を実行する（または相互作用する）、コンポーネント付きのニューラルネットワークを設計しトレーニングすることができます。このアイデアは 『視覚的注意の再帰型モデル』 で初めて紹介されました。一連の低解像度の中心窩による一瞥（人間の目から着想されたもの）から画像を処理したモデルの例を挙げています。特に、イテレーションごとに、再帰型ニューラルネットワーク（RNN）は画像中の小さな1部分を受け取り、次を見るための位置をサンプリングします。例えば、RNNは(5,30)を探し、画像を受け取り、それから(24,50)を見に行くと決める、などです。この問題は、ネットワークの一部分が、次はどこを探索するかの分布を生成し、そこからサンプリングするというものです。残念ながら、この処理は微分不可能です。もし別の位置からサンプリングしたら何が起っていたか、私たちは直感的には分からないからです。大まかに、入力から出力までのニューラルネットワークを考慮してみてください。

注釈：
ネットワークの前方パス
入力
微分可能な演算
微分不可能な演算（確率的方策からの例）

通常、ほとんどの矢印（青）は微分可能ですが、トランジションの中には微分不可能なサンプリング処理（赤）もあります。青い矢印をバックプロパゲーションするのには問題がありませんが、赤い矢印はバックプロパゲーションできない依存関係を表現しています。

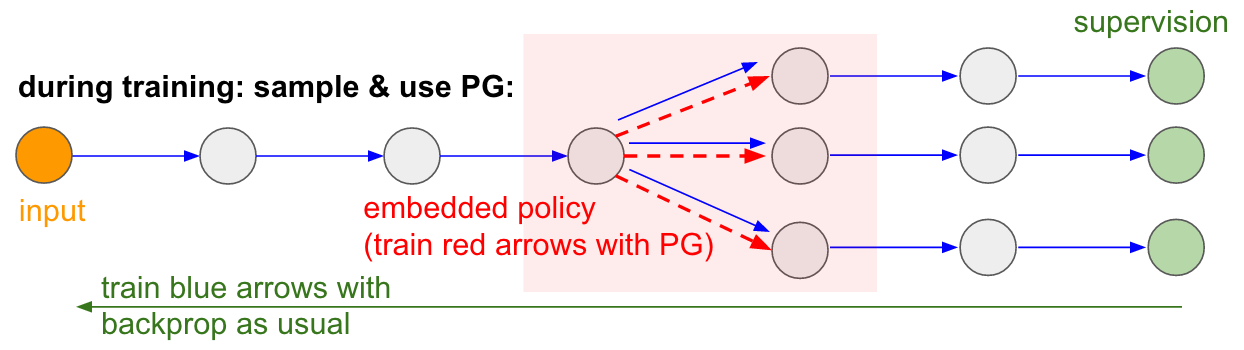
ここで方策勾配が役に立ちます。より広いネットワークに埋め込まれた小さい確率的方策としてサンプリングするネットワークの一部分について考えましょう。これは、トレーニングの間いくつかの（下記の図で示されるような）サンプルを生成し、サンプルがいずれ良い結果（図の例で言うと最後の損失によって測定される）に導かれるよう促します。言い換えると、青い矢印に関わるパラメータは通常通りバックプロパゲーション法でトレーニングし、赤い矢印に関わるパラメータは方策勾配を用いた後方パスによって独立して更新され、損失を少なくするサンプルを促進しています。この考えについては 『確率論的演算グラフを用いた勾配評価』 によくまとめられています。

注釈：
トレーニングの間：PGを使ったサンプリング
入力
埋め込まれた方策（PGで赤い矢印をトレーニングする）
教師あり学習
通常のバックプロパゲーションで青い矢印をトレーニングする

トレーニング可能なメモリI/O。 このテーマについても多くの論文で見ることができます。例えば、 ニューラルチューリングマシン（NTM) は読み書きするためのメモリテープを備えていて、書き込み処理は m[i] = x と実行されます。この時、 i と x はRNNコントローラネットワークによって予測されます。しかし、この処理は微分不可能です。違う位置、 j != i に書き込んだ場合、損失がどうなってしまったか通知するシグナルがないからです。ですから、NTMは ソフト的 な読み出し／書き込み処理をしなくてはなりません。これは注意分配 a を予測し（足すと1になる0と1の間の要素を使い、書き込みたいインデックスを割り出す）、 for all i: m[i] = a[i]*x を実行します。これで微分可能になりました。しかし私たちは演算上の重い代価を払わなくてはなりません。1つの位置に書き込むためだけに、1つ1つのメモリセル全てにアクセスしなくてはならないからです。コンピュータの全ての課題がRAM全体にアクセスしなくてはならないことを考えてみてください。

しかし、 RL-NTM でしたように、方策勾配を使ってこの問題を（理論上は）回避できます。私たちはまだ注意分配 a を予測しますが、ソフト的に書き込みをする代わりに、 i = sample(a); m[i] = x に書き込むように位置をサンプリングします。トレーニングの間、私たちはこれを少量の i のバッチに対して実行し、最後には一番うまくいった分岐の状態にするのです。演算の大きな優位点は、テストの時に、1カ所を読み出し、または書き込みするだけで良くなる点です。しかし論文で指摘されている通り、この手法を機能させるのは困難です。サンプリングを通してアルゴリズムを使うと、偶発的な滞りが必ず出てくるからです。最近の共通認識では、PGがうまく機能するのは、広大な探索範囲から絶望的なサンプリングをしなくなるように個別の選択を少なくした設定の時だけです。

しかし、大量のデータ、または演算が利用可能なケースでは方策勾配法を使うと、大体の場合において可能性が大きく広がります。例えば、LaTeXのコンパイラ（char-rnnで、コンパイルを行うLaTeXを生成したい場合など）やSLAMシステム、LQRソルバなどの大きくて微分不可能なモジュールと相互作用するよう学習するニューラルネットワークの設計が可能です。または、超知能が世界を乗っ取るのに必要な重要な情報にアクセスするために、TCP/IPを介してインターネットとやりとりする学習を望むかもしれません（残念なことに、これは微分不可能です）。これは、いい例ですね。

まとめ

ここまでで、方策勾配法は強力だということと、一般的なアルゴリズムを説明してきました。また1つの例として、ATARI製『ポン』のエージェントを生のピクセルから、ゼロから作り上げた 130行のPython を用いてトレーニングしました。もっと一般的に、同じアルゴリズムを使って任意のゲームのエージェントをトレーニングできます。いつか、数多くの大切な現実世界の制御問題で役に立つ日がくるでしょう。最後に、いくつか大切な事項を追記したいと思います。

最先端のAI 。このアルゴリズムで行うのは、「最初にランダムなジッタが発生したあと、少なくとも一度、理想的には繰り返し何度も成功体験を繰り返し、方策の分布がパラメータ変化を通じて望ましい動作を繰り返す方向に移行する」という力づくの探索である、ということを見てきました。また、人間がこれらの問題に取り組む場合は全く違う方法を取ることも見てきました。これは、高速に抽象モデルを構築しているかのようでした。つまり、（多くの人が試しているにも関わらず）研究の表面的な部分をかろうじて引っ掻いたという感じです。これらの抽象モデルは明示的なアノテーションが（不可能でなかったとしても）とても難しいため、近頃では多くの人が（教師なしの）生成モデルやプログラムの導入に強い興味を示しています。

複雑なロボットの問題設定での使用 。このアルゴリズムは、膨大な量の探索が難しい状況に対してはそのままスケールすることができません。例えば、1台(ないし数台)のロボットがあり、リアルタイムに世界とやりとりするような状況などです。このようなケースでは、私がこの投稿で述べたようにアルゴリズムを単純適用するのは難しいのです。この問題を緩和するための関連研究として、 決定論的方策勾配法 があります。確率論的な方策からサンプルを引き出して高得点を取ることを促すのではなく、決定論的な方策を使い、スコア関数を形成するセカンド・ネットワーク（ クリティック と呼ばれています）から勾配の情報を直接入手します。原則的に、サンプリング・アクションの範囲が狭い、高次元のアクションを伴う問題設定において、このアプローチは非常に効果的です。しかし、ここまで見た限り、これを機能させるのは少し厄介かなと思います。別の関連するアプローチには、ロボット工学をスケールアップする方法が挙げられます。まずは、 Googleのロボットのアーム工場 、もしくは テスラのモデルSに搭載されたオートパイロット機能 について学ぶことから始めましょう。

他にも、教師を追加することで探索過程での絶望を和らげてくれるという方法があります。例えば、多くの事例において、人間から専門家のやり方を得ることができます。例として AlphaGo（アルファ碁） は最初に教師あり学習を用いて、棋士の対戦における人間の動きを予測していました。しかし後に、人間のマネをするという方策は、対戦に勝つという”実際”の目標に方策勾配法を用いて微調整されました。ケースによっては専門家のやり方がほとんどない場合（例えば ロボットの遠隔操作 など）があります。そして、 徒弟学習 の下でデータを活かすための技術も必要です。最後に、教師ありのデータが人間から全く提供されない場合は、費用のかかる最適化の技術で計算するというケースもいくつかあります。例えば、力学モデルとして知られる軌道の最適化（物理シミュレータにおけるF=maなど）などを使います。もしくは、おおよその局所力学モデルを学習するケースもあります（将来的に非常に期待できる 誘導方策探索 のフレームワークで確認できます）。

実践でのPGの使用 。これが最後の追記事項です。RNNのブログでやりたかったことをしたいと思います。私は、RNNは魔法で、自動的に任意の連続的な問題に取り組んでいるという印象を与えられたと自負しています。しかし、実際はこれらのモデルを機能させることは難しく、注意と専門知識が必要です。そして、多くのケースがやりすぎで、本来ならもっとシンプルな方法でもここで述べた90パーセント以上の成果を得ることができます。方策勾配法にも同じことが言えます。これは自動ではありません。数多くのサンプルが必要で、永遠にトレーニングを繰り返し、うまく機能しない時のデバッグが困難です。バズーカ砲を手に取る前に、繰り返しBB弾を試すべきです。強化学習では、常に最初に試すべき強力なベースラインは 交差損失エントロピー法（CEM） です。これは単純な確率による山登り法の「推測してチェックする」という手法で、開法によっておおまかな範囲が決められます。どうしても方策勾配法で問題に取り組みたい場合は、論文の tricks の項に細心の注意を払ってください。まず簡単なことから始め、PGのバリエーションの1つ、 TRPO を使います。これは、どんな場合でも大体うまく機能し、 実践において 通常のPGよりも確実です。考え方の核となるのは、方策を過剰に変更するパラメータのアップデートを避けることです。これは、データのバッチ上で従来の方策と新しい方策によって予想された分布の間にあるKLダイバージェンス上の制約によって強制的に行われます（共役勾配法の代わりに、この考えを最も単純に具体化する方法は、直線探索と並行してKLのチェックを行うことかもしれません）。

これで終わりです。現在の強化学習の状況や、変化がどんなものかということを、お伝えできていれば幸いです。そして、もしRLの向上に貢献したいと思っていただけたなら、ぜひ OpenAI Gym をご利用ください。それでは、次回をお楽しみに。