(訳注：2016/6/28、記事を修正いたしました。)

本記事は、もう随分と前から投稿したいと思っていた強化学習（RL）に関するものです。RLは盛り上がっています。皆さんも既にご存知のこととは思いますが、今やコンピュータは ATARI製ゲームのプレイ方法を自分で学習する ことができ（それも生のゲーム画像のピクセルから！）、 囲碁 の世界チャンピオンにも勝つことができます。シミュレーションの四肢動物は 走って飛び跳ねる ことを学習しますし、ロボットは明示的にプログラミングするのが難しいような 複雑な操作のタスク でも、その実行方法を学習してしまいます。こうした進歩はいずれも、RL研究が基となって実現しています。私自身も、ここ1年ほどでRLに興味を持つようになりました。これまで、 Richard Suttonの著書 で勉強し、 David Silverのコース を通読、 John Schulmannの講義動画 も閲覧しました。 JavascriptでRLのライブラリ も書きました。夏の間はDeepMind社のDeepRLグループでインターンとして働き、つい最近では新しいRLのベンチマークツールキット、 OpenAI Gym の設計／開発に少し参画しました。というわけで、少なくとも1年は間違いなくこの楽しいワゴンに乗っていたのですが、これまでは、なぜRLが重要なのか、RLはどういうものか、どのように開発されて、どこに向かうのか、といったことについて短い記事を書く時間的余裕もありませんでした。

実際のRLの例。 左から： Deep Q-Learning networkによりプレイされているATARI製ゲーム、AlphaGo、レゴを積み重ねるバークレーロボット、身体的なシミュレーションにより地形を飛び越える四肢動物。

RLにおける近年の進歩の本質をよく考えることは興味深いものです。私はAIを制御する要因について、4つの独立した要因として考えるのが好きです。

1. 演算（これは明らかですね。：ムーアの法則、GPU、ASIC）
2. データ（いい形式で、インターネット上のどこかにあるものだけではなく、例えばImageNetなど）
3. アルゴリズム（研究やアイデア、例えばバックプロパゲーション、CNN、LSTM）
4. インフラストラクチャ（お使いのソフトウェア、例えばLinux、TCP/IP、Git、ROS、PR2、AWS、AMT、TensorFlowなど）

RLにおける進歩について、皆さんは「新たな驚くべきアイデアに突き動かされて起こっている」と思われるかもしれませんが、そうではありません。そして、これはコンピュータビジョンの分野で起こったことと同様なのです。コンピュータビジョンのケースでは、2012年のAlexNetは、ほぼ「1990年のConvNetの(深さ・広さの)スケールアップ版」と言えます。同様に、2013年からのATARI Deep Q-Learningに関する論文も標準的なアルゴリズム(関数近似を加えたQ学習。1998年Suttonが著したスタンダードなRLの本で見つけることができます)を実装したものにすぎませんし、そこで用いられている関数近似もConvNetです。AlphaGoはモンテカルロ木探索（MCTS）の方策勾配法を使っていますが、これらもまた標準的な構成要素です。もちろん、それを機能させるためには多くのスキルと忍耐を要するだけでなく、古いアルゴリズムに加えて複数の巧妙なひねりも開発されてきましたが、大まかに見れば、最近の進歩の立役者はアルゴリズムではなく、演算／データ／インフラストラクチャです（コンピュータビジョンと同様です）。

では、話をRLに戻しましょう。まるで魔法のように感じられるものが、ふたを開けてみたら、なんてシンプルなものだったのか、といったギャップがあると、私はいつもそわそわして心底このブログの記事にしたくなります。今回、ATARI製ゲームのプレイの仕方を人間と同じレベルで、1つのアルゴリズムで、ピクセルから、ゼロから自動的に学習することができるなんて信じられないという人を多く見てきました。確かにそれは驚くべきことであり、私も同じように考えていました。しかし、私たちが使っているアプローチも、コアの部分では本当にかなり愚直なものです（後からそんな主張をするのは簡単だと分かっていますが）。とにかく、現時点でRLの問題を解決するために、私たちが最初に好んで選択する方策勾配法（PG）をご紹介したいと思います。RLにそれほど詳しくないという方は、なぜ私が代わりにDQNを説明しないのかと気になるかもしれないですね。DQNとは、また別の選択肢で、より良く知られているRLアルゴリズムであり、 ATARI製ゲームを扱う論文 により幅広く普及したものです。Q-Learningが素晴らしいアルゴリズムというわけではないことが分かります（DQNは2013年だと言うかもしれませんね（いいでしょう、50％はジョークとします））。実際、多くの人が方策勾配法を好みます。オリジナルのDQNの論文を書いた著者もそうです。彼は、方策勾配法（PG）がうまく調整された場合、Q-Learningよりもうまく機能することを 示し ました。PGは最初から最後までできるため好まれているのです。明確な方策と期待される報酬を直接最適化する理にかなったアプローチがあります。とにかく、実行されている例として、PGで、ゼロから、ピクセルを用いて、深層ニューラルネットワークを用いたATARI製ゲーム（『ポン』）のプレイの仕方を学習します。最終的なコードは、依存ライブラリとしてNumpyだけを利用する、130行だけのコードになります。（ Gist link ）。では、やってみましょう。

ピクセルから『ポン』

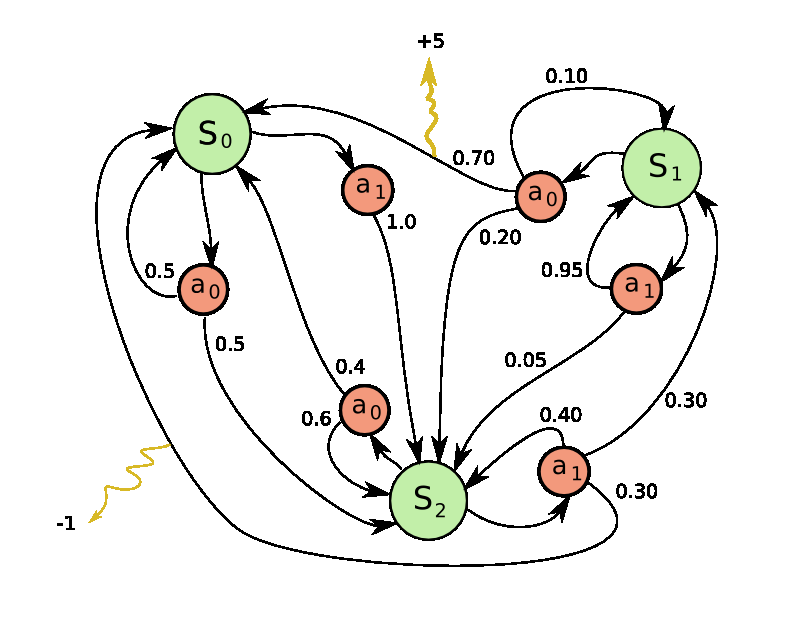
左： ゲーム『ポン』。 右： 『ポン』は マルコフ決定過程（MDP） の特別なケース。グラフは各ノードが特定のゲームの状態で、各エッジが可能な推移（一般的な確率で）となっている。また、各エッジは報酬を与え、どんな状態でもその報酬を最大にするために最適なアクションを計算することが目標。

ゲーム『ポン』は単純なRLタスクの優れた例です。ATARI 2600バージョンでは、あなたのプレイを片方のパドルに用います（もう片方はまともなAIによって制御される）。あなたは相手が返したボールを打ち返さなければなりません（本当に『ポン』を説明する必要はないですかね？）。次のように低いレベルでゲームが動きます。画像フレーム（ 210x160x3 のバイト配列（ピクセル値を与える0から255までの整数））を受け取ったら、私たちはパドルを上に（UP）動かしたいか下に（DOWN）動かしたいかを決めます（つまり、2値の選択です）。1つ1つの選択後にゲームシミュレータはアクションを実行し、私たちに報酬を与えます。ボールが相手側のパドルをすり抜けたら追加点1、自分側がボールを通してしまったら減点1、そのどちらでもなければ0、という具合です。もちろん、目標はたくさんの報酬を得られるようにパドルを動かすことです。

ご注意いただきたいのは、この問題を解くにあたり、用意する『ポン』についての仮定をとても少なくしようとしているところです。本当のところ、『ポン』自体はあまり気にしていません。気になるのは、ロボット操作やアセンブリ、ナビゲーションのように複雑で高次元な問題です。『ポン』はいつか偶然にも役に立つタスクができる、ごく一般的なAIシステムの書き方を見つけ出しつつ、私たちも遊べるという、単なる楽しいおもちゃのテストケースなのです。

方策ネットワーク。 まず、プレイヤ（または「エージェント」）を実装する 方策ネットワーク を定義しましょう。このネットワークはゲームの状態を受けて、私たちが何をすべきかを決めます（UPあるいはDOWNへの移動）。好ましいシンプルな計算として、生の画像ピクセル（計100,800（210×160×3））を入力とする2層のニューラルネットワークを使い、UPに行く確率を示す1つの数値を生成します。これは、単にUPに移動する 確率 を出したということであり、 確率論的な 方策を使用するための基準であることに注意してください。インタラクションごとにこの分布からサンプリングして（バイアスがかかったコインを投げるようなものです）実際の動きを決定します。この理由は、トレーニングの話をすれば明らかになるでしょう。

注釈
raw pixels：生のピクセル
hidden layer：隠れ層
probability of moving UP：UPに移動する確率
ここでの方策ネットワークは2層の完全に接続されたネットワークである。

ここで具体的にするため、PythonのライブラリNumpyでこの方策ネットワークを実装する方法を示します。（前処理された）ピクセル情報を持つベクトル x を与えられているとします。そこで次のように計算します。

h = np.dot(W1, x) #隠れ層のニューロンの活性化を算出
h[h<0] = 0 #ReLU非線形性：閾値0
logp = np.dot(W2, h) #UPに行く確率の対数を算出
p = 1.0 / (1.0 + np.exp(-logp)) #シグモイド関数（UPに行く確率を与える）

このスニペットにおいて、 W1 と W2 はランダムに初期化された2つの行列です。大したことではないので、バイアスは使っていません。最後には シグモイド 非線形を使うことに注意してください。確率のアウトプットは範囲[0,1]です。直感的には、（ W1 の列に沿って配置される重みがある）隠れ層のニューロンは様々なゲームのシナリオを検出することができます（例えば、ボールは一番上にあり、パドルは中ほどにあるなど）、さらに W2 の重みはそのとき、それぞれの場合に、UPに行くべきかDOWNに行くべきかを決めます。さて、初期のランダムな W1 と W2 はもちろん、その場でプレイヤを迷わせます。そのため、現在の唯一の問題は『ポン』のプレイヤのエキスパートにつながる W1 と W2 を見つけることなのです。

Fine print：前処理。 理想的には、動きを検出できるようにするため、方策ネットワークに少なくとも2フレームを送りたいところです。もう少し簡単にするために（私はMacBookでこれらの実験を行いました）、前処理のほんの少しをやろうと思います。実際にネットワークに 差分フレーム を送ります（つまり、現在のフレームと最後のフレームの引き算です）。

これは、不可能なように思えます。 ここで、RLの問題がいかに難しいということを認識してもらいたいと思います。私たちは100,800個の数字（210×160×3）を得て、方策ネットワークに転送します（この方策ネットワークは、 W1 と W2 に100万ものオーダーのパラメータを容易に含みます）。UPに行くと決めたとして、ゲームは「このタイムステップでは報酬が0」というレスポンスを返し、さらに次のフレームのまた別の100,800個の数値を返します。0以外の報酬が得られるまで、数百回のタイムステップにわたりこのプロセスを繰り返すことになるかもしれません。例えば、最終的に1という報酬を獲得したとします。それは素晴らしいですが、どうしてそうなったのかということをどのように説明できるでしょうか？たった今とった行動によるものでしょうか？それとも、76フレーム前でしょうか？あるいは、10フレーム目と90フレーム目に関係していたのでしょうか？さらに、将来的にはもっと良いものにするためにと、100万ものノブのうちどれを変更すべきで、それはどのようにしたらできるのかということは、どう解決するのでしょうか？私たちはこれを、 “credit assignment problem（貢献度分配問題）” と呼びます。『ポン』の具体的なケースでは、ボールが相手側のパドルをすり抜ければ追加点1を得られることを知っています。 真の 原因は「私たちが良い軌道でボールを跳ね返したから」ということですが、実際のところその操作はかなり前のフレームで行われたものです。『ポン』のケースで言えば20フレームほど前の操作がそれにあたり、その後で行った1つ1つのアクションは結局のところ、報酬を得るかどうかに対し影響はありませんでした。言い換えれば、非常に難しい問題に直面し、見通しはとても暗いと言えます。

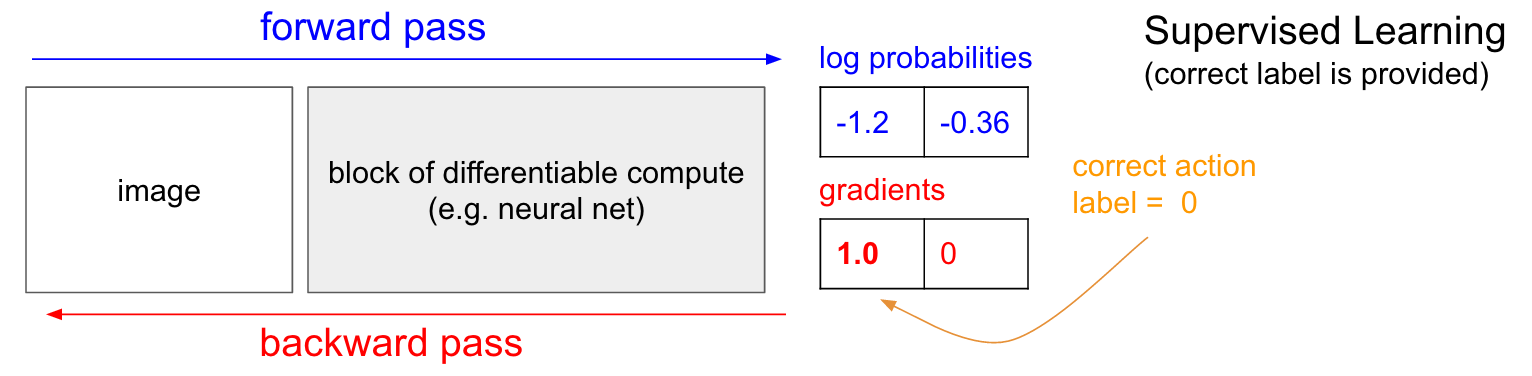
教師あり学習。 早速、方策勾配法（PG）についてお話ししたいところですが、その前に、簡単に教師あり学習について思い出していただきたいと思います。なぜなら、ご覧のとおり、RLは非常に似ているからです。以下の図を見てください。通常の教師あり学習では、ネットワークに画像を与え、いくつかの確率を得ます。例えばUPとDOWNの2つのクラスの確率です。常に正しいラベルの確率の対数を最適化するため（これが計算をより良くし、対数は単調なので生の確率を最適化することと同じです）、生の確率（30％と、この場合は70％）の代わりにUPとDOWNの確率の対数（-1.2、-0.36）をお見せしましょう。さて、教師あり学習で、私たちにはラベルを得ることができます。例えば、今すぐ行うべき正しいことはUPに行く（ラベル0）ことであると言われるかもしれません。実装では、UPの確率の対数に1.0の勾配を入力し、勾配ベクトル\(\nabla_{W} \log p(y=UP \mid x) \)を計算するためにバックプロパゲーションを実行します。この勾配が、ネットワークがUPを予測する可能性をわずかに高めるために、100万のパラメータの1つ1つをどうやって変更するべきかを教えてくれます。例えば、ネットワークにおける100万のパラメータのうちの1つが-2.1の勾配を持つなら、それはつまり、小さな正の量（例えば 0.001 ）によってそのパラメータを増やしていった場合、UPの確率の対数は 2.1×0.001 （負符号により減少）減少することを意味します。その後パラメータをアップデートすると、やりました、私たちのネットワークはもう、将来非常に類似した画像を見ればUPを予測するという可能性がわずかに高くなります。

注釈
forward pass：前方パス
backward pass：後方パス
image：画像
block of differentiable compute：微分可能な演算のブロック
e.g. neutral net：例えばニュートラルネットワーク
log probabilities：確率の対数
gradients：勾配
Supervised Learning：教師あり学習
correct label is provided：正しいラベルが提供される
correct action：正しいアクション
label：ラベル

方策勾配法。 いいですね、しかし強化学習の状況下で正しいラベルを持っていない場合はどうしたらよいでしょうか？方策勾配法があります（もう一度、以下の図を見てください）。私たちの方策ネットワークはUPに行く確率が30％、（確率の対数-1.2）とDOWNに行く確率が70％（確率の対数-0.36）と算出しました。今、この分布から動作をサンプリングします。例えば、サンプルとしてDOWNが得られ、ゲームでそれを実行したとします。この時点で、1つの興味深い事実に気が付きます。すぐに私たちは教師あり学習で行ったようにDOWNの1.0の勾配を入力し、将来DOWNのアクションを行う可能性がわずかに高いネットワークになる勾配ベクトルを見つけることができます。つまり、私たちはすぐにこの勾配を評価することができます。それは素晴らしいことですが、問題はDOWNに行くことが良いのかどうか、とにかく今の時点では分からないということです。しかし、重要なのは、単に少し待てばそれが分かるので、大丈夫だということです。『ポン』の例ではゲーム終了まで待つことができ、その後、然るべき報酬を得ることができます（勝てば追加点1、負ければ減点1のいずれか）。さらに、私たちが選んだアクションに対する勾配としてそのスカラを入力します（この場合はDOWN）。以下の例では、DOWNに行くと、私たちは結局ゲームに負けることになります（報酬は減点1）。そのため、DOWNの確率の対数に対し-1を入力してバックプロパゲーションを行うことで、このネットワークに将来同じインプットがあった時にDOWNのアクションを選択するのを 阻止する 勾配を見つけることになるでしょう（当然そうです。そのアクションにより私たちはゲームに負けたのですから）。

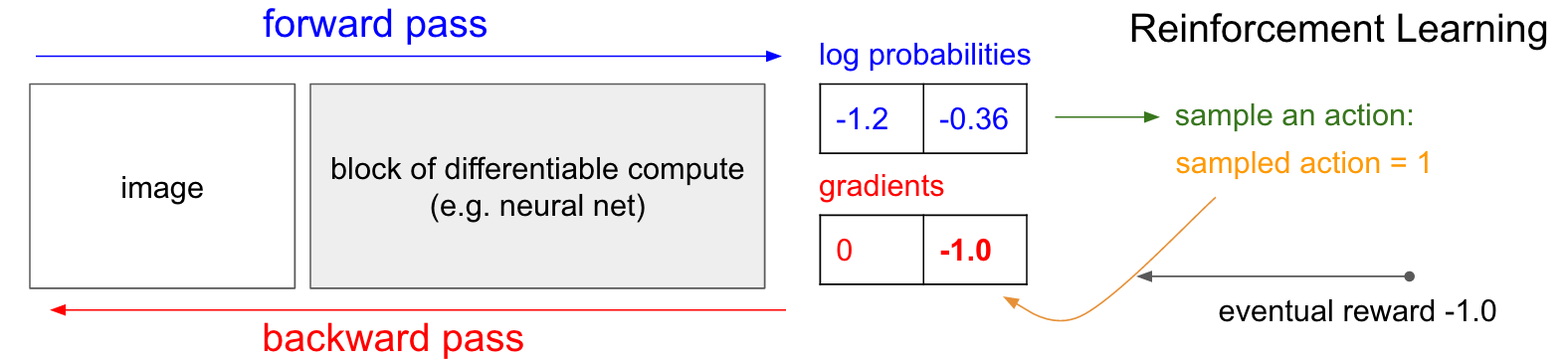
注釈
Forward pass：前方パス
Backward pass：後方パス
Imag：画像
Block of differentiable comput：微分可能な演算のブロック
Eg. Neutral ne：例えばニュートラルネットワーク
Log probabilities：確率の対数
Gradients：勾配
Reinforcement learning：強化学習
Sample an action：サンプリングするアクション
Sampled action：サンプリングされたアクション
Eventual reward：最終報酬

そして、これだけなのです。確率的な方策を持っておき、そこから動作をサンプリングします。その動作のうち、最終的によい結果に至ったものは将来的にも奨励することにし、逆に最終的に悪い結果に至ったものは将来的に回避することにします。また、最終的にゲームに勝てば、報酬が+1でも-1でも関係ないのです。最終結果の質を表す任意の指標を代わりに用いることができます。例えば、もし全ての結果が良ければ10.0とし、これを減点1の代わりに勾配として入力してバックプロパゲーションを開始することができます。これがニュートラルネットワークの良さなのです。そのため、使うことは少しズルのようにも思えます。確率的勾配降下法（SGD）を使えば、100万のパラメータを1TFLOPS（テラフロップス）の演算に埋め込むことが可能になり、任意のことを実行することもできます。できそうにもない物事ですが、面白いことに我々が住む世界ではこれが可能なのです。

トレーニングの手順。 では、どのようにトレーニングが行われるのか、詳しく説明します。方策ネットワークを W1 や W2 で初期化し、『ポン』を100ゲームします（これらの方策を”ロールアウト”と呼びます）。各ゲームが200フレームで構成されていると仮定すると、UPに動かすのかDOWNに動かすのかの判断は20,000必要となり、さらに、各判断のパラメータ勾配は分かっているので、将来同じ状況に置かれた場合に同様の判断を下せるためにはどうパラメータを変更すればいいのかも分かります。残るのは、それぞれの判断を、どのように良い判断と悪い判断にラベルできるようにするかです。例えば、12勝88敗だったとします。全ての判断、200×12=2400の判断が勝利したゲームで下されたことになり、これをプラス更新します（サンプリングされたアクションの勾配を追加点1とし、バックプロパゲーションとパラメータ更新をして、これらの状態で選択したアクションを奨励します）。そして、敗北した分の200×88 = 17,600判断をマイナス更新します（先ほどとは反対に、取ったアクションを避けるようにします）。以上です。これで、ネットワークは成功した方のアクションを繰り返す傾向になり、失敗したアクションを避ける傾向になります。ここで、新しく、少し改善された方策で徹底的に100ゲームを遂行することができます。

方策勾配：方策をしばらく実行。どのアクションにより高い報酬が得られるかを確認し、確率を増加させる。

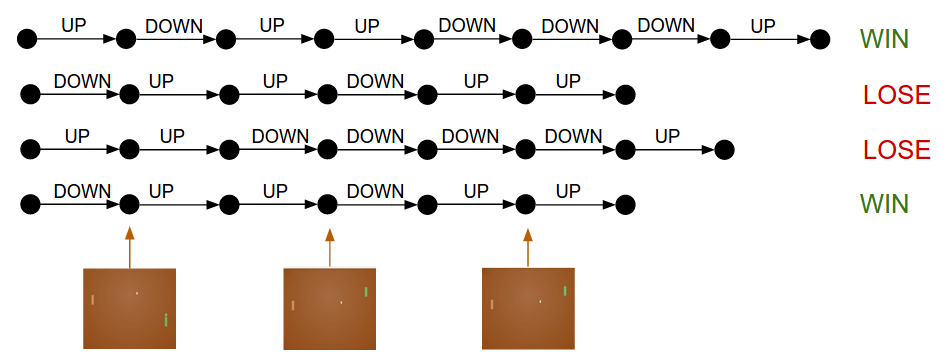
4つのゲームのダイアグラムです。ここでは、サンプリングしたアクションの状態遷移を表しています。それぞれの黒い丸はゲームの状態を表し（例として3つの状態を下の部分に箱で可視化しています）、そしてそれぞれの矢印に注釈を付けてどのように遷移したのか表しています。この例では、2勝2敗となっています。方策勾配によって、勝利したゲームで取ったアクションを推奨します。反対に、敗北したゲームで取ったアクションは控えるようにします。

一連のプロセスを考えると、おかしな性質に気が付くと思います。例えば、50フレーム目でいいアクションを取った（正しくボールを打ち返した）けれども、その後、150フレーム目でミスした場合はどうでしょう。敗北したため、アクションが全て悪いとラベルされてしまい、正しくボールを打ち返した50フレーム目でのアクションも阻止するものとされてしまうのでしょうか。もちろん、そうなってしまいます。しかしながら、何千、何万ものゲームでプロセスを考えた時、最初の打ち返しが正しければ、勝利する傾向が強くなり、平均すると正しく打ち返すためのプラス更新の方がマイナス更新より多くなり、結果、正しい決断をする方策になるのです。

さらに一般的なアドバンテージ関数 ：返り値についてさらに詳しく説明するとお約束しました。ここまでは、勝利したゲームをベースにそれぞれのアクションを 良い ものと判断しました。一般的な強化学習の条件においては、報酬\(rt\)をそれぞれの段階で取得します。よく使われる方法の一つが割引報酬で、上の図にある”最終報酬”の数式は\( Rt = \sum_{k=0}^{\infty} \gamma^k r_{t+k} \)となり、\(\gamma\)は割引率と呼ばれる0から1の間の値（例えば0.99）になります。この数式は「サンプリングされたアクションの奨励の度合いは、後で得る報酬の重み付き合計である」ということを示していますが、これではより後での報酬が指数関数的に重要でなくなります。実用の上では、これらを正規化することも重要となります。例えば、上で示したような『ポン』のロールアウト100個について、20,000全てのアクションの\(R_t\)を計算するとします。ここでは、バックプロパゲーションをする前に、返り値を”標準化”する（例えば平均値を引いて標準偏差で割る）のが名案と言えます。このようにすれば、常に実行済みのアクションの半数を推奨したり阻止したりすることが可能になります。数学的にはこれを解釈すると、方策勾配推定量の分散を制御することになります。詳細は こちら をお読みください。

方策勾配の導き方。 方策勾配の数学的背景について簡単に説明します。方策勾配は一般的な スコア関数の勾配推定量 の特殊なケースを指します。一般的な場合、\(E_{x \sim p(x \mid \theta)} [f(x)] \)という数式で スコア関数の勾配推定量 は表現されます。例えば、何らかの\(theta\)でパラメータ化された確率分布\(p(x;\theta)\)のもとで、スカラ値をとるスコア関数\(f(x)\)の期待値などです
。お分かりだと思いますが、\(f(x)\)が報酬関数（より一般的に言えばアドバンテージ関数）で、\(p(x)\)が方策ネットワークです。そしてこの\(p(x)\)は\(p(a \mid I)\)のモデルとなり、あらゆる画像\(I\)に対する動作の分布を与えます。ここで気になるのが、どのようにすれば、分布（パラメータ\(\theta\)をとおして）を変更して、\(f\)によって決められるサンプリングの得点を上げられるのかです（例えば、どのようにネットワークのパラメータを変更すれば、サンプリングした動作の得点は上げられるのかです）。次の数式があります。

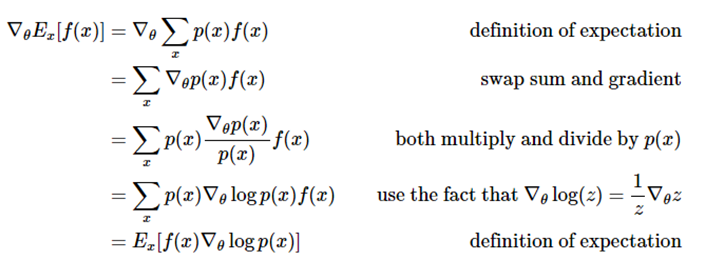
期待値の定義⇒勾配と総和の入れ替え⇒\(p(x)\)で乗算・除算⇒\(\nabla_{\theta} \log(z) = \frac{1}{z} \nabla_{\theta} z\)を利用⇒期待値の定義

分かりやすく言うと、サンプリング可能な何らかの確率分布\(p(x;\theta)\)(以降は\(p(x)\)と略記します)があるとします(例えば正規分布など)。それぞれのサンプルから、サンプルを引数に取ってスカラ値を返すスコア関数\(f\)を評価することができます。この数式では、\(f\)によって決められる得点を上げたい場合、どのように分布を（パラメータ\(\theta\)を通じて）変更すればいいのかを示しています。ここで特に強調しているのは、いくつかのサンプル\(x\)を書き、それぞれのスコア\(f(x)\)を評価し、さらに、第2項の\( \nabla_{\theta} \log p(x;\theta) \)に対してもそれぞれの\(x\)を評価しているということです。この第2項とは何なのでしょうか。これは、ある\(x\)について、パラメータ空間で確率を増加する方向を示す勾配のベクトルです。つまり、\(\theta\)を\( \nabla_{\theta} \log p(x;\theta) \)の方向に少しずつ動かすと、新しく\(x\)に割り当てられた確率が少し上昇しているのが分かります。数式をもう一度見てみると、この方向に向かってスカラ値の得点\(f(x)\)を掛ければいいのです。これで、低得点のサンプルよりも、高得点のサンプルの確率密度を強く”引っ張る”ことになるので、複数のサンプルの\(p\)確率密度を使って更新すると、高得点の方向に移行し、高得点のサンプルの可能性を高めます。

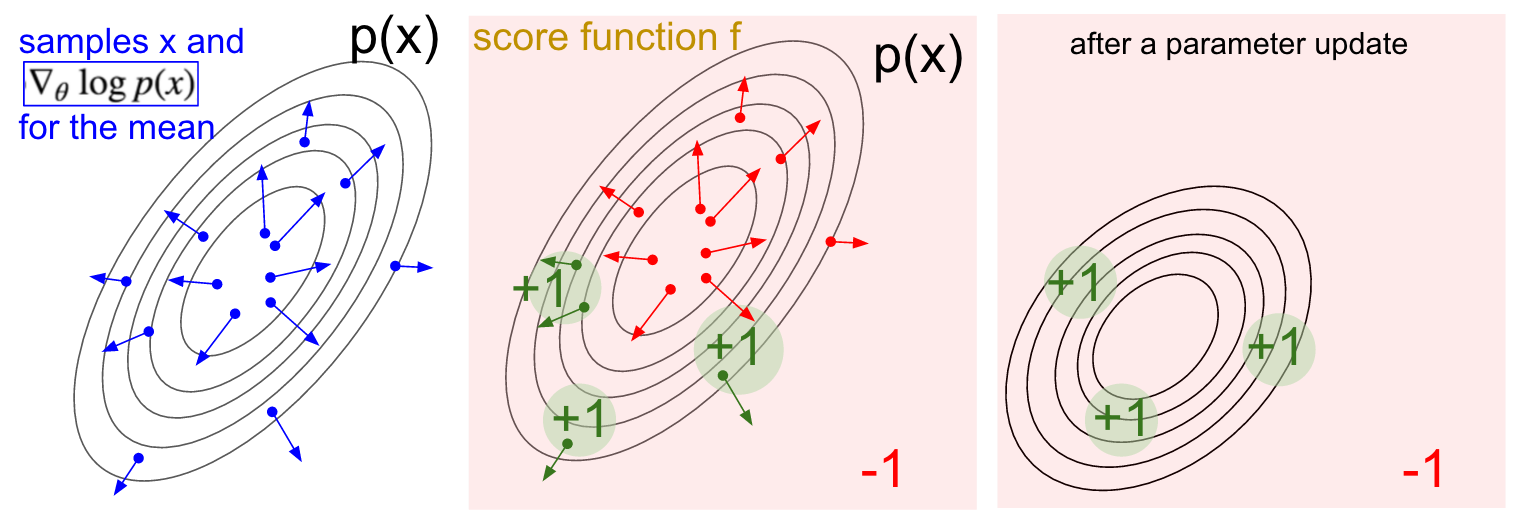
注釈
samples \(x\) and\( \nabla_{\theta} \log p(x;\theta) \)for the mean：ある平均値に対するサンプル\(x\)と\( \nabla_{\theta} \log p(x;\theta) \)

スコア関数の勾配推定量の可視化。 左： 正規分布とそこから得たサンプル（青点）。それぞれの青点に、正規分布の平均値パラメータに対応する、対数形式で表現された確率を割り当てます。矢印は、「そのサンプルの確率を上げるためには、正規分布の平均値がどの方向に引っ張られるべきか」を示しています。 中： 減点1となっているスコア関数と、追加点1となっているいくつかの小さな領域のオーバーレイ（注意：これは任意で、必ずしも微分可能なスカラ関数ではありません）。ここでは矢印を色分けして更新の倍数の上下を表します。緑の矢印の平均は上がり、赤の矢印は マイナス 方向に向かいます。 右： パラメータ更新後、緑の矢印と逆向きの赤の矢印によって、全体が左下へと引っ張られます。この分布からのサンプルは、望みどおり、より高いスコアが期待されます。

強化学習との関連が理解できたと思います。方策ネットワークは動作のサンプルを提供し、場合によっては、提供に差が出るかもしれません（アドバンテージ関数によります）。このちょっとした数学から、「方策のパラメータを変更するには、まずロールアウトをいくつか実行し、サンプリングされた動作から勾配を取得し、スコアを乗算して全てを合算すればよい」ということが分かりますし、上記でやってきたことはまさにこれです。さらに詳しく導き方や説明を読みたい方は、 John Shculmanの講義 をお勧めします。

学習。 ここまで方策勾配に対する直感を鍛え、さらには、どのように導き出されるのかを見てきました。アプローチ全体を 130行から成るPythonのスクリプト に落とし込みました。ここでは、 OpenAI Gym のATARI『ポン』2600版を使っています。1バッチ10エピソードに対して、RMSPropを使って200の隠れ層のユニットがある、2層方策ネットワークに学習させました（どちらのプレイヤでも21点まで得点できるので、それぞれのエピソードは数十のゲームで構成しています）。ハイパーパラメータのチューニングはそれほどせず、自分の（遅い）MacBookを使った実験を行いましたが、3夜連続で学習を続けると、AIプレイヤよりも賢い方策を作成することができました。エピソード合計は約8,000だったので、アルゴリズムで『ポン』を20万回ゲームをした計算になり（結構な数ですよね）、その結果、更新は最高で800回されました。友人曰く、もしGPU上で畳み込みニューラルネットワークを用いて数日間で学習させることができるのであれば、AIプレイヤに勝てる確率は上がり、さらに、ハイパーパラメータの最適化をうまくできれば、常にAIプレイヤに勝つことができるそうです（例えば全勝するとか）。しかしながら、演算や調整に時間をかけることがでませんでした。でも、主なアイデアを説明できる『ポン』AIを作ることはでき、非常にうまく機能します。

学習したエージェント(緑のもの、右)と決め打ちされたAI（左）を相手に対戦しています。

学習された重み付け。 学習された重み付けについても見てみましょう。前処理をしたため、インプット1つ1つが80×80の差分画像になります（現在のフレームから1つ前のフレームを除算した差分）。 W1 の全ての行を取り、80×80にして可視化します。下にあるのは、（200分の）40ニューロンをグリッドにしたものです。白ピクセルは正の重みであり、黒ピクセルは負の重みです。いくつかのニューロンがボールの特定のバウンドの軌跡にチューニングされ、線に沿って黒と白の交互に符号化されていることに注意してください。ボールは1カ所でしか存在できないので、ニューロンがマルチタスクで動作し、ボールの動線に沿った複数の箇所で”発火”します。ボールがこの軌跡に沿って移動すると、ニューロンの動作も正弦波として変動し、正規化線形関数（ReLU)のため、トレースに沿った個別の離れた場所から”発火”することになるので、この黒と白が交互になっているのは面白いです。画像に少しの乱れがありますが、これは、L2正則化すれば軽減できたのでしょう。

後編はこちら： 深層強化学習：ピクセルから『ポン』 – 後編