2015年11月17日
より良いビジネス意思決定のために、機械学習の閾値を可視化する

(2015-10-09)by Slater Stich
本記事は、原著者の許諾のもとに翻訳・掲載しております。
機械学習のモデルを構築した際、データサイエンティストとしての私たちの最終的なゴールは価値の創造でした。モデルが無かった(あっても今より原始的だった)頃よりも、何かしら良いものを生み出すためにモデルによる予測を活用したいのです。結果に焦点を当てるということはつまり、私たちのモデルのパフォーマンスの最終的な評価は、その有効性によって為されるということです。それは、モデルを利用したアプリケーションが生み出した価値の量として計測されます。この投稿では、ビジネスの価値を最大限にするモデル構築による意思決定を、選択したり理解したりする際の強力なツールとして、データの可視化を活用したいと思います。
分類アルゴリズムにおいて、最も一般的な利用パターンの1つが 閾値(しきいち) です。閾値以上のスコアを持つ全てのケースに対して、何らかの特別な処置を行うのです。以下に例を挙げます。
- 不正の防止: あなたはソーシャルネットワークの企業に勤めていて、偽のアカウントを削除したいと考えています。そこで分類器を構築し、0から1の値をとる”不正スコア”を各アカウントに対して割り当てます。調査後、スコアが0.9より高い全てのアカウントを、偽アカウント対応チームに送付します。チームは各ケースをチェックし、実際に偽のアカウントであれば削除します。
- 反応のモデル化: あなたは新進のソフトウェア企業に勤めていて、対外セールスプログラムを改良したいと考えています。そこで、顧客候補の膨大なデータベースを購入し、分類器を構築して、自社のセールスチームが営業を行った場合に、自社製品を買う可能性のある顧客を予測します。そして”反応スコア”が閾値0.7より高い全ての顧客に対して電話をかけるように決定します。
- ショッピングカートの放置: あなたはeコマースの企業に勤めていて、ショッピングカートを放置したまま、購入手順に進まないユーザに対して10%の割引クーポンを送ろうと考えています(何とか購入手順に進むユーザには10%の割引クーポンを送りたくありません。価格の10%が損失となるからです)。そこで、購入に進まないユーザを予測する分類器を構築します。そして”放置スコア”が0.85より高いユーザに対して10%の割引クーポンを送るように決定します。
- その他
閾値の算出はシンプルで実装が楽なのでよく利用されます。私たちは連続的なスコアをイエス/ノーの二者択一に変換します。そして所定の方法で、その結果に対処します。
閾値の算出パターンにおける最大の問題は、 閾値をどの位置に設定すべきか、ということです。 これは予測の問題というよりも、ビジネス上の決断なので、あらゆるケースに当てはまるような答えはありません。しかしこの投稿では、自分自身で正しい決断を下すのに役立つ、可視化の方法をご紹介したいと思います。
閾値による決定の可視化
閾値の位置を決める際に、考慮すべき要素が3つあります。
- キュー率: どれくらいのケースを処理したいですか? これは、全体的な処理能力にもよりますし、それとともに個別のケースを取り扱うコストにもよります。偽の可能性のあるアカウントの調査をチームに依頼している場合は、フラグを立てられるケース数はチームの人数によって制限されます。制限時間内でチームはどれだけのケースを調査できるでしょうか。そうではなくて、もし大量のeメールを送るためのものでしたら、変動費用はほとんどゼロです。多くのケースをキューする余裕があります。
- 適合率: 間違ってケースをキューした際に、何が損失となるでしょうか? 偽のアカウントを調査している場合は、調査時間が損失コストです。もし間違って10%の割引クーポンを、商品購入を終えようとしている人に送ってしまったとしたら、ショッピングカート内の商品の10%が損失コストです。
- 再現率: キューするべきケースをキューしなかったら、何が損失となるでしょうか? セールスの手掛かりをキューしているならば、失ったセールスの機会の価値が損失です。偽のアカウントを調査しているならば、ネットワーク内に偽のアカウントがあることで生じるコストに、損失は関係します。
これら全ての要素を一度に理解するために、分類器の閾値の関数としてキュー率、適合率、再現率を表すグラフを描いてみたいと思います。そうすれば異なる閾値に直面した時に、トレードオフが簡単に分かりますし、自分の個別の状況に応じて最適な選択ができます。
これを実例で見るために、かの有名な 通信事業者のチャーンデータセット を見てみましょう。このデータセットには契約者の電話のプランに関する情報が含まれています。最終目標は、どのユーザが次回の契約期間の前に解約するかを予測することです(その前に考えておくことがあります。解約を予測できることの価値は何でしょうか。この予測を基にどんな行動ができるでしょうか。その答えは、企業の優先度と解約を防止することの価値によりますが、いくつかアイデアはあります。つまり、10ドルの割引クーポンを解約の危険性の高いユーザに送り、もし今、新たに12か月の契約をしてくれたら割引をしますと提案します。または、さらに契約を12か月延長してくれるようなユーザには、新たな電話購入に対して補助金を出すように提案します。他にもいろいろあります)。
それではこの問題を解決する分類器を構築しましょう。独自のランダムフォレストモデルを使用します。
# Imports
import pandas as pd
import numpy as np
from sklearn.cross_validation import train_test_split
from sklearn.ensemble import RandomForestClassifier
from sklearn.metrics import precision_recall_curve
from sklearn.preprocessing import LabelEncoder
# データセット取得
df = pd.read_csv('http://www.dataminingconsultant.com/data/churn.txt')
# 前処理
df.columns = [c.lower().replace(' ', '_').replace('?', '').replace("'", "") for c in df.columns]
state_encoder = LabelEncoder()
df.state = state_encoder.fit_transform(df.state)
del df['phone']
binary_columns = ['intl_plan', 'vmail_plan', 'churn']
for col in binary_columns:
df[col] = df[col].map({
'no': 0
, 'False.': 0
, 'yes': 1
, 'True.': 1
})
# 分類器の構築、そして予測
clf = RandomForestClassifier(n_estimators=50, oob_score=True)
test_size_percent = 0.1
signals = df[[c for c in df.columns if c != 'churn']]
labels = df['churn']
train_signals, test_signals, train_labels, test_labels = train_test_split(signals, labels, test_size=test_size_percent)
clf.fit(train_signals, train_labels)
predictions = clf.predict_proba(test_signals)[:,1]では、閾値の関数としての、このモデルのパフォーマンスを見てみましょう。 sklearn の便利な関数、 precision_recall_curve を使います。
precision, recall, thresholds = precision_recall_curve(test_labels, predictions)
thresholds = np.append(thresholds, 1)
queue_rate = []
for threshold in thresholds:
queue_rate.append((predictions >= threshold).mean())
plt.plot(thresholds, precision, color=sns.color_palette()[0])
plt.plot(thresholds, recall, color=sns.color_palette()[1])
plt.plot(thresholds, queue_rate, color=sns.color_palette()[2])
leg = plt.legend(('precision', 'recall', 'queue_rate'), frameon=True)
leg.get_frame().set_edgecolor('k')
plt.xlabel('threshold')
plt.ylabel('%') 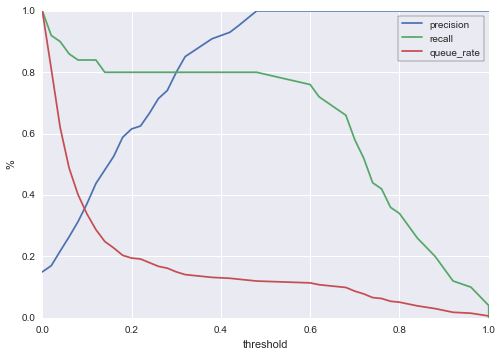
このグラフの読み方をご説明します。x軸の閾値に対して、キュー率、適合率、再現率の割合がy軸に表されています。例えば、0.4の閾値を選択します(スコア0.4以上の全てのケースに対して、調査や送付や提案など、近いうちに何らかの対処を行うということです)。すると、
- 約14%のケースがキューとなります。もし解約するアカウントが一日あたり10,000あるとして、そのうち約1,400件が特別に対処するアカウントとして選ばれることになります。
- 適合率は約92%です。この場合、もし対処しなければ、キューとしたケースの92%が本当に解約することになります。
- 再現率は約80%です。このモデルによって、次の契約期間の前に解約する全てのユーザの、80%を捕捉することができます。
もちろんこの会社にとって、0.4は最適な閾値ではないかもしれません。例えば、期間内に500ケースしか対処できないとします(この仮説の10,000ケースの5%です)。すると、閾値は0.8のあたりを選択しなければなりません。その場合、適合率は100%に跳ね上がりますが、再現率は35%程度にまで落ちます。重要なのは、このグラフによって、十分な情報を得た上で閾値を決められるようになったということです。
モデルの可変性を扱う
上で作成したグラフは、トレーニングとテストのデータ分割1セットのみでのパフォーマンスを示しています。このサンプルがモデルのパフォーマンスをほぼ忠実に示していることを期待したいのですが、起こりうるパフォーマンスの幅を知るためにもデータの分割を行ったサンプルをいくつも作成し可視化するべきでしょう。最も簡単なのは、何度もランダムにデータを分割し、分割のたびに曲線をプロットする方法です。以下は、通信事業のチャーンモデルについてランダムに50回分割を行った場合の結果を示したものです。
clf = RandomForestClassifier(n_estimators=50, oob_score=True)
n_trials = 50
test_size_percent = 0.1
signals = df[[c for c in df.columns if c != 'churn']]
labels = df['churn']
plot_data = []
for trial in range(n_trials):
train_signals, test_signals, train_labels, test_labels = train_test_split(signals, labels, test_size=test_size_percent)
clf.fit(train_signals, train_labels)
predictions = clf.predict_proba(test_signals)[:,1]
precision, recall, thresholds = precision_recall_curve(test_labels, predictions)
thresholds = np.append(thresholds, 1)
queue_rate = []
for threshold in thresholds:
queue_rate.append((predictions >= threshold).mean())
plot_data.append({
'thresholds': thresholds
, 'precision': precision
, 'recall': recall
, 'queue_rate': queue_rate
})
for p in plot_data:
plt.plot(p['thresholds'], p['precision'], color=sns.color_palette()[0], alpha=0.5)
plt.plot(p['thresholds'], p['recall'], color=sns.color_palette()[1], alpha=0.5)
plt.plot(p['thresholds'], p['queue_rate'], color=sns.color_palette()[2], alpha=0.5)
leg = plt.legend(('precision', 'recall', 'queue_rate'), frameon=True)
leg.get_frame().set_edgecolor('k')
plt.xlabel('threshold')
plt.ylabel('%') 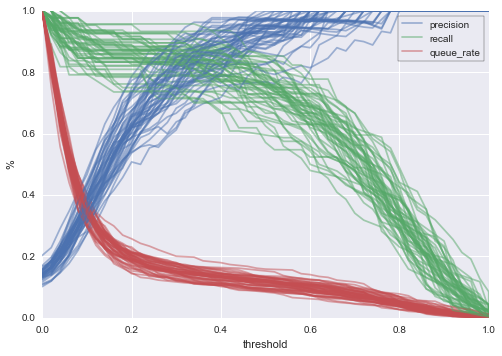
予想通り、いくつかのバリエーションが確認できました。先ほどは、トレーニングとテストのデータに分割したサンプルを1つだけ見て、閾値が0.4の場合の見解を次のように説明しました。
- キュー率 14%
- 適合率 92%
- 再現率 80%
新しいグラフでは値にもっと幅ができます。50回分割を行った結果を示す新しいグラフを確認してください。閾値0.4の場合に次のことが言えます。
- キュー率 10%から20%
- 適合率 70%から100%
- 再現率 60%から90%
統計的に可視化することで、更に正確に説明することもできます。それぞれの閾値に対して90%の中央区間と共に中央値の曲線をプロットしてみましょう。
import bisect
from scipy.stats import mstats
uniform_thresholds = np.linspace(0, 1, 101)
uniform_precision_plots = []
uniform_recall_plots= []
uniform_queue_rate_plots= []
for p in plot_data:
uniform_precision = []
uniform_recall = []
uniform_queue_rate = []
for ut in uniform_thresholds:
index = bisect.bisect_left(p['thresholds'], ut)
uniform_precision.append(p['precision'][index])
uniform_recall.append(p['recall'][index])
uniform_queue_rate.append(p['queue_rate'][index])
uniform_precision_plots.append(uniform_precision)
uniform_recall_plots.append(uniform_recall)
uniform_queue_rate_plots.append(uniform_queue_rate)
quantiles = [0.1, 0.5, 0.9]
lower_precision, median_precision, upper_precision = mstats.mquantiles(uniform_precision_plots, quantiles, axis=0)
lower_recall, median_recall, upper_recall = mstats.mquantiles(uniform_recall_plots, quantiles, axis=0)
lower_queue_rate, median_queue_rate, upper_queue_rate = mstats.mquantiles(uniform_queue_rate_plots, quantiles, axis=0)
plt.plot(uniform_thresholds, median_precision)
plt.plot(uniform_thresholds, median_recall)
plt.plot(uniform_thresholds, median_queue_rate)
plt.fill_between(uniform_thresholds, upper_precision, lower_precision, alpha=0.5, linewidth=0, color=sns.color_palette()[0])
plt.fill_between(uniform_thresholds, upper_recall, lower_recall, alpha=0.5, linewidth=0, color=sns.color_palette()[1])
plt.fill_between(uniform_thresholds, upper_queue_rate, lower_queue_rate, alpha=0.5, linewidth=0, color=sns.color_palette()[2])
leg = plt.legend(('precision', 'recall', 'queue_rate'), frameon=True)
leg.get_frame().set_edgecolor('k')
plt.xlabel('threshold')
plt.ylabel('%') 
これで、閾値0.4に対して、ずっと正確な説明ができるようになりました。
- 90%の確率で、キュー率11%から15%となり、中央値は13%
- 90%の確率で、適合率80%から95%となり、中央値は90%
- 90%の確率で、再現率70%から85%となり、中央値は80%
このグラフを使うと、実際の状況で異なる閾値の結果を比べるのと同じように、多くのことが分かります。
経営者のように、閾値を設定する
最後に説明したグラフについて、私が特に気に入っているところは、機械学習の結果に基づき、ビジネス上の決定力を与えてくれる点です。モデルを構築するという技術的な役割を超え、このモデルを使って実際に何を行うかを決定する役割が与えられるのです。上のグラフと、簡単なコストや利益の分析が少しだけあれば、すぐに始められます。
簡単な例を挙げてみましょう。皆さんの会社で、顧客が他社のサービスに乗り換えるのを防ぐための対策として、乗り換える危険の高い顧客に個別にダイレクトコールをかけるとします(設定した閾値以上のチャーンスコアのユーザを対象とします)。説明を分かりやすくするために、非現実的ですがこの対策はいつも効果的に機能していると仮定しましょう。つまり他社に乗り換えようとしていたユーザは、電話をもらうと乗り換えをしないと仮定します。この対策チームには3人のメンバーがいて、期限内にかけられる電話の回数は、それぞれ333回だとします。すると、期限内に合計で1,000回の電話をかけられることになります。さらに、各期限に10,000のケースが存在し、電話を1回かけるごとにメンバーに支払う金額を20ドル、ユーザが1人乗り換えると失う金額が100ドルだとします。私たちの目的に対して、この見積りが完璧である必要はありません。簡単な計算方法が好ましいです。
では、グラフを見てみましょう。閾値を0.57に設定したとします。するとキュー率は10.03%=1,003ケースとなり、これが扱える全てのケースとなります。そしてグラフでは不確定な要素も示されます。お分かりかと思いますが、閾値0.57の場合、キュー率には8.4%=840ケースから11.4%=1,140ケースまで変化する可能性があります。あらかじめ皆さんのチームが絶対に1,000ケース以上扱えないと分かっている場合は、閾値を変更することもできます。90%の区間が1,000ケースの制限を超えないように低めの閾値(例えば0.65など)を選んでください。
更にもう少し重要な話をします。グラフを確認していただくと、上限が1,000コールという処理能力は、皆さんのビジネスにとって最適ではないことが分かるはずです。なぜなら再現率が非常に低くなっているからです。では、総費用が20ドル×1,000=20,000ドルで適合率が96%とすると、0.96×100ドル×1,000=96,000ドルの売り上げとなり、このオペレーションで得られる総利益は76,000ドルとなります。しかし、もし予算が2倍あったらどうでしょう? 20,000ケースのレビューが可能となり、かかる費用は4万ドル、適合率は61%で売り上げは0.61×100ドル×2,000=122,000ドル、利益は約82,000ドルとなります。このグラフは、 毎期 6,000ドルを稼ぎ出す手助けとなるのです。
これは、より良い閾値を選ぶための知識に基づく推論です。もう少し、色々と調べてみると、この見積りに対して最適な閾値は0.33であることが分かりました。これを中央値で計算すると約90,700ドルが得られることとなります。
uniform_thresholds = np.linspace(0, 1, 101)
uniform_payout_plots = []
n = 10000
success_payoff = 100
case_cost = 20
for p in plot_data:
uniform_payout = []
for ut in uniform_thresholds:
index = bisect.bisect_left(p['thresholds'], ut)
precision = p['precision'][index]
queue_rate = p['queue_rate'][index]
payout = n*queue_rate*(precision*100 - case_cost)
uniform_payout.append(payout)
uniform_payout_plots.append(uniform_payout)
quantiles = [0.1, 0.5, 0.9]
lower_payout, median_payout, upper_payout = mstats.mquantiles(uniform_payout_plots, quantiles, axis=0)
plt.plot(uniform_thresholds, median_payout, color=sns.color_palette()[4])
plt.fill_between(uniform_thresholds, upper_payout, lower_payout, alpha=0.5, linewidth=0, color=sns.color_palette()[4])
max_ap = uniform_thresholds[np.argmax(median_payout)]
plt.vlines([max_ap], -100000, 150000, linestyles='--')
plt.ylim(-100000, 150000)
leg = plt.legend(('payout ($)', 'median argmax = {:.2f}'.format(max_ap)), frameon=True)
leg.get_frame().set_edgecolor('k')
plt.xlabel('threshold')
plt.ylabel('$')
plt.title("Payout as a Function of Threshold")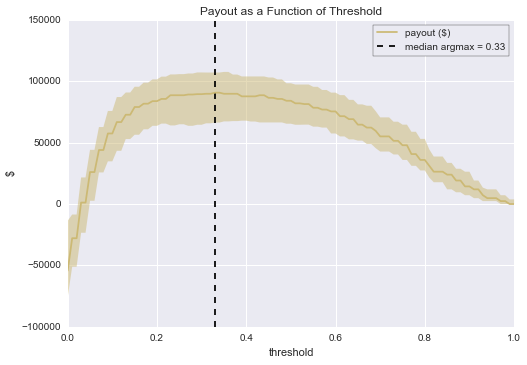
オペレーションの利益性には多くの不確定要素があることも既に分かっています。前もってこれを想定し、自然に起こりうるケースが起こった場合に自信を持って対処できるようにしましょう。
(追記として、説明した方がいいことがあります。分類器の一般的なデフォルト値である0.5をそのまま使った場合(例:チャーンスコアが0.5以上のケースはキューに入れ、0.5未満は無視する)、閾値のグラフで可能とされる値よりも、ずっと低い利益しか得られません。閾値が0.5で、それに合う処理能力の場合、89,200ドルではなく、得られるのは約84,000ドルで、毎期5,000ドル以上も違うのです! )
一般的に、キュー率/適合率/再現率のグラフを使うと、オペレーションやモデルの最善の使い方を戦略的に決める際、”条件を変えたらどうなるか? ”という分析が簡単になります。
まとめ
閾値は、機械学習を用いた分類器から価値を導き出す簡単で効果的な方法です。閾値を用いる場合は、本稿でご紹介したようにデータを可視化する技術を使うと、選択可能な閾値のトレードオフを、それぞれ知ることができます。それが、皆さんの個々のビジネスアプリケーションが最高の価値を創出するため、閾値を選ぶ時の一助となるのです。
本稿用のIPython notebookは こちらからご利用できます 。

