2016年10月20日
情報理論を視覚的に理解する (3/4)
(2015-10-14)by Christopher Olah
本記事は、原著者の許諾のもとに翻訳・掲載しております。
交差エントロピー
オーストラリアへ引っ越す直前、Bobは、私が作ったもう1人の人物、Aliceと結婚しました。私も、私の頭の中の他のキャラクターたちも驚いたことに、Aliceは犬好きではありませんでした。彼女は猫好きだったのです。それにもかかわらず、2人は、それぞれ動物に夢中で、非常に語彙が限られているという共通点を見出したのでした。
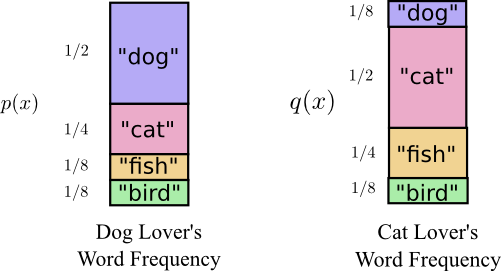
注釈:犬好きが使う単語の頻度 猫好きが使う単語の頻度
2人は、同じ単語を使いますが、その頻度だけは異なります。Bobはいつも犬の話をしているし、Aliceは猫の話ばかりしています。
最初に、AliceがBobのコードを使ったメッセージを私に送ってきました。あいにく、そのメッセージは必要以上に長いものでした。Bobのコードは彼の確率分布に最適化されていました。Aliceは別の確率分布を持っており、Bobのコードを使うのは最適とは言えません。Bobが自身のコードを使う際のコードワードの平均的な長さは1.75ビットであるのに対し、Aliceが彼のコードを使うと平均2.25ビットになります。2人がそれほど似ていなければ、もっと悪い状況になっていたでしょう。
この長さ(ある分布から事象を交信する際に、他の分布に最適なコードを用いた場合の平均的な長さ)は、交差エントロピーと呼ばれます。交差エントロピーは、次の公式で定義できます。 ^(1)
\[H_p(q) = \sum_x q(x)\log_2\left(\frac{1}{p(x)}\right)\]
この場合、犬好きのBobの単語の頻度に対する、猫好きのAliceの単語の頻度の交差エントロピーです。

注釈:交差エントロピー: \(H_p(q)\)
\(p(x)\) のコードを使った \(q(x)\) のメッセージの長さの平均
コミュニケーションのコストを下げるため、Aliceに自分のコードを使うよう頼みました。すると、彼女のメッセージの長さ平均が下がり、私はホッとしました。しかしこれは新たな問題をもたらしました。時折、Bobが誤ってAliceのコードを使ってしまうようになったのです。しかも驚くことに、Bobが間違ってAliceのコードを使うほうが、Aliceが彼のコードを使う場合よりも状況が悪化したのでした。
ここで考えられる可能性は4つです。
- 自分のコードを使うBob \((H(p) = 1.75 ~\text{bits})\)
- Bobのコードを使うAlice \((H_p(q) = 2.25 ~\text{bits})\)
- 自分のコードを使うAlice \((H(q) = 1.75 ~\text{bits})\)
- Aliceのコードを使うBob \((H_q(p) = 2.375 ~\text{bits})\)
これは必ずしも、感覚的に分かるものではありません。たとえば、 \(H_p(q) \neq H_q(p)\) などです。では、以上4つの値の相互関係を表すにはどうすればよいでしょうか。
次の図表で、それぞれのサブプロットはこれら4つの可能性の1つを表しています。各サブプロットはメッセージの平均の長さを先の図表がしたのと同じように可視化しています。四角形で整理しているので、メッセージが同じ分布から来ている場合はプロットは隣同士に並び、同じコードを使っている場合は、上下に並びます。こうして、分布とコードを視覚的に一緒にスライドさせることができます。
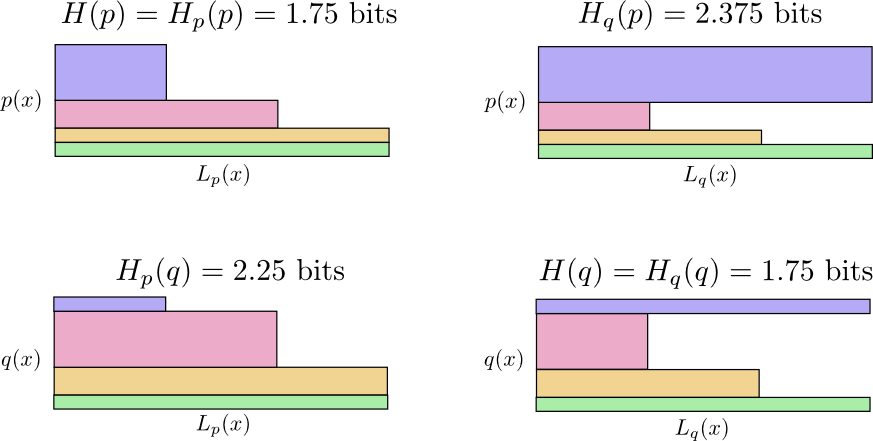
\(H_p(q) \neq H_q(p)\) になる理由は分かりますか? \(H_q(p)\) が大きいのは、 \(p\) 下で非常によく起こるものの、 \(q\) 下では稀なためコードが長い事象(青色)があるためです。一方で、 \(q\) 下でよく起こる事象は \(p\) 下ではまれなものの、その差分は極端ではないので、 \(H_p(q)\) はそれほど高くないのです。
交差エントロピーは対称ではありません。
では、なぜ交差エントロピーを考慮しなければならないのでしょうか。それは、交差エントロピーが2つの確率分布がいかに異なっているかを表現する手段になるからです。 \(p\) と \(q\) の分布が違っているほど、 \(p\) の \(q\) に対する交差エントロピーは \(p\) のエントロピーよりも大きくなるでしょう。
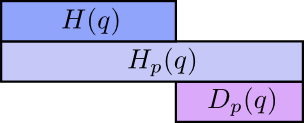
同様に、 \(p\) が \(q\) と異なれば異なるほど、 \(q\) の \(p\) に対する交差エントロピーは \(q\) のエントロピーよりも大きくなります。
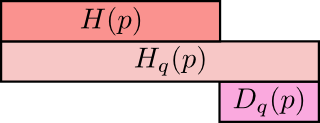
とても面白いのは、エントロピーと交差エントロピーの差です。その違いは、別の分布用に最適化したコードを使ったことによって、どれほどメッセージが長くなるかを示しています。分布が同じであれば、この違いはゼロになります。差が広がるにつれ、長さも大きくなっていきます。
この差をKullback–Leibler情報量、あるいは単にKL情報量と呼びます。 \(q\) に対する \(p\) のKL情報量、 \(D_q(p)\) ^(2) は次のように定義されます ^(3) 。
\[D_q(p) = H_q(p) – H(p)\]
KL情報量が非常に巧みなのは、それが2つの分布の間の距離のようであることです。KL情報量は分布の差異を測るのです(この考え方を突き詰めると、情報幾何学になります)。
交差エントロピーとKL情報量は、機械学習の分野で大変役に立ちます。ある分布を別の分布に近づけたい事例はよくあるからです。例えば、予測した分布を正解データに近づけられないかと考えることがあるでしょう。KL情報量を使えばそれが当然のように実現できるので、様々なところで利用されています。
エントロピーと多変数
先の天候と服装の例に戻りましょう。
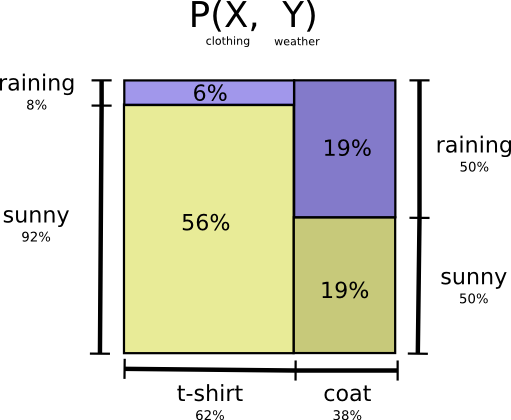
多くの親と同じく、母は私が天候にふさわしくないものを着ているのでは、と心配します(その疑いには理由があって、私はよく冬場にコートを忘れるのです)。ですから母は、天候と私が着るものの両方をしばしば知りたがるということです。これを伝えるためには、彼女に何ビット送ればよいでしょうか。
簡単に考えるには、確率分布を平坦化することです。
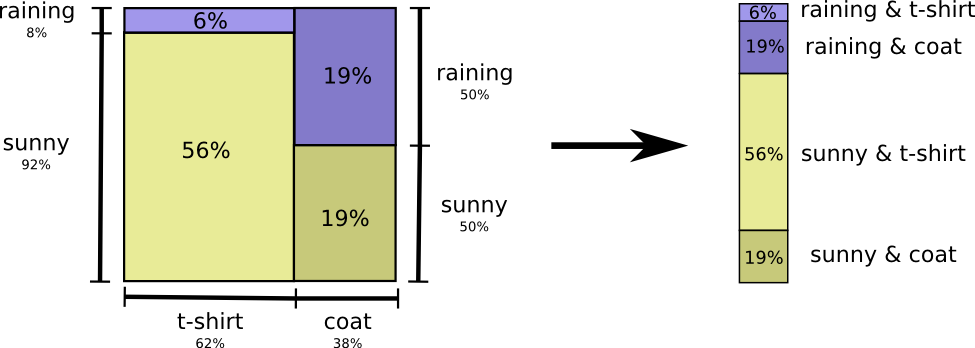
これで、これら確率の事象に最適なコードワードが分かり、メッセージの長さの平均を計算できます。
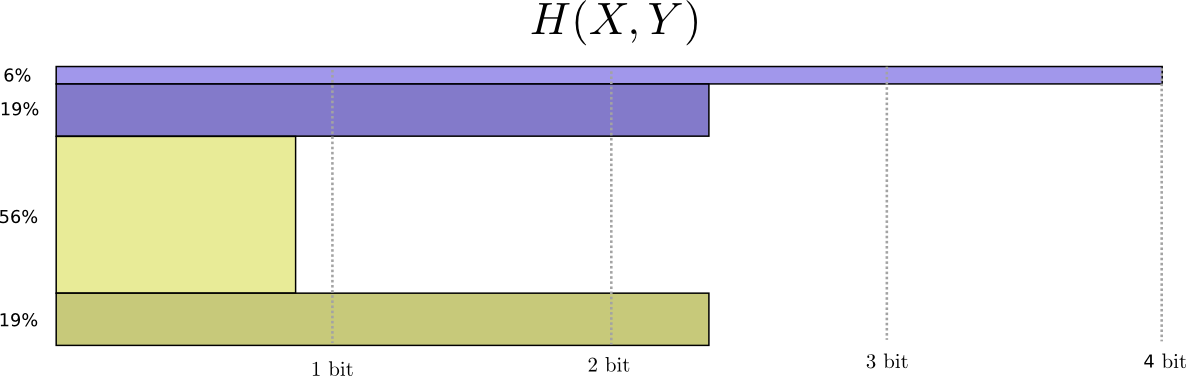
これは、確率変数 \(X\) と \(Y\) の結合エントロピーと呼ばれ、次のように定義されます。
\[H(X,Y) = \sum_{x,y} p(x,y) \log_2\left(\frac{1}{p(x,y)}\right)\]
これは、1つではなく2つの変数があること以外は、通常の定義と全く同じです。
もう少しばかり良い考え方は、分布を均すのを避け、コードの長さを3次元として見ることです。エントロピーが体積になりました。
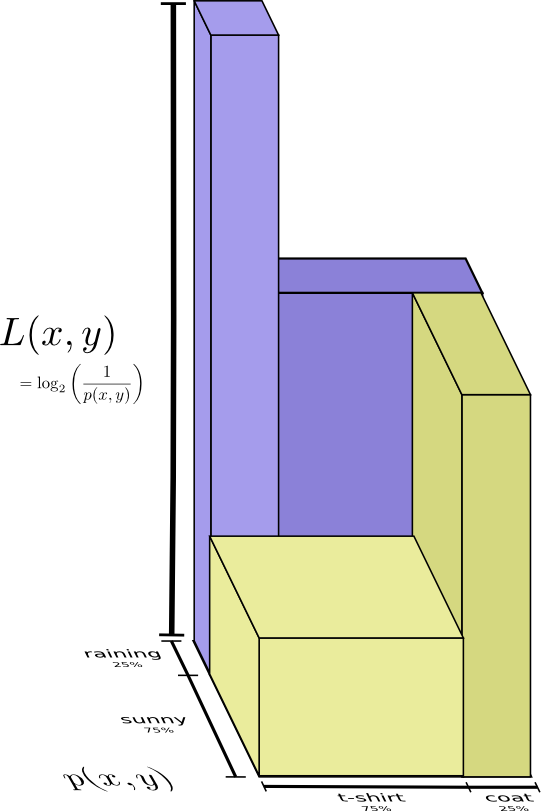
しかし、母が既に天候を知っているとしましょう。ニュースでチェックしたのです。この場合、与えるべき情報はどれほどでしょうか。
やはり、自分が着る服を伝達するため、多くの情報を送る必要があるように見えます。しかし、天候は私が着るであろう服装をはっきりと示唆するので、より少ない情報の送信で済むのです。雨の場合と晴れの場合を分けて考えてみましょう。
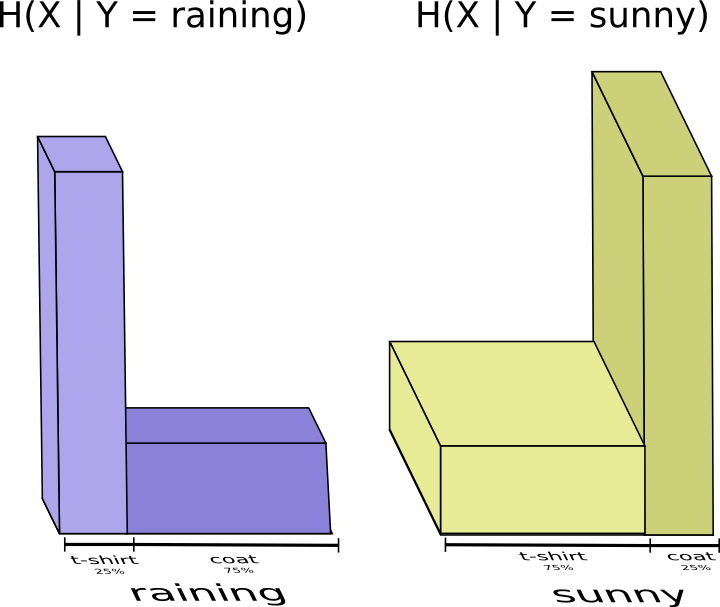
雨でも晴れでも、概して多くの情報を送る必要はありません。なぜなら、天候が分かれば正解を推測しやすいからです。晴れの時は、晴れに最適化した特別なコードを使い、雨の時は雨に最適化したコードを使います。どちらの場合も、両方のための汎用コードを使うのに比べ、送る情報は少なくなります。母親に送る平均的な量の情報を取得するには、これら2つのケースを一緒にすればよいのです…。
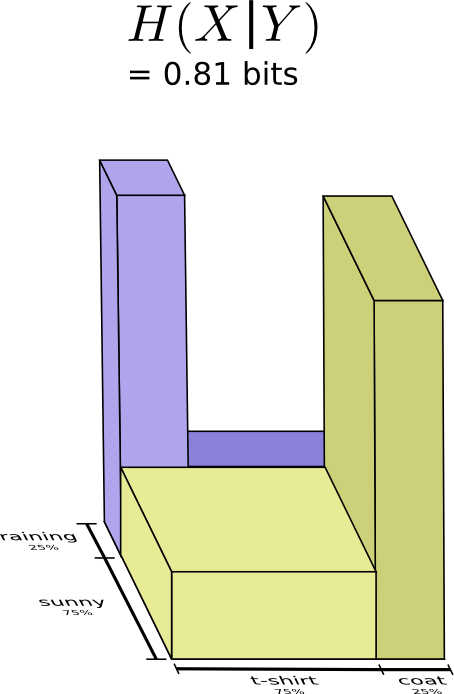
これを条件付きエントロピーと呼びます。公式に落とし込むと次のようになります。
\[H(X|Y) = \sum_y p(y) \sum_x p(x|y) \log_2\left(\frac{1}{p(x|y)}\right)\] \[~~~~ = \sum_{x,y} p(x,y) \log_2\left(\frac{1}{p(x|y)}\right)\]
相互情報量
前の章で、変数の1つを知っていれば、もう1つの変数はより少ない情報で伝達できることを見てきました。
これについて考える時に良い方法は、情報の量を帯としてイメージすることです。互いの間に共有する情報がある場合、それらの帯は重なり合います。例えば、 \(X\) と \(Y\) が持つ情報に共有部分がある時、 \(H(X)\)と \(H(Y)\)は重なり合うのです。そして、 \(H(X,Y)\) は両方に存在する情報なので、 \(H(X)\)と \(H(Y)\)の帯の和集合です。 ^(4)
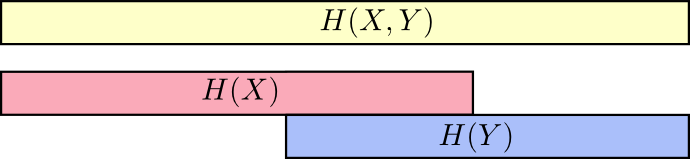
上記のように考えると、多くのことが分かりやすくなります。
例えば、「 (X) と (Y) の両方を伝える場合(”結合エントロピー”: \(H(X,Y)\) )に必要な情報の量は、 \(X\) のみを伝える場合(”周辺エントロピー”: \(H(X)\))よりも多くなる」ということを前述しました。しかし、既に \(Y\) を知っているなら、それを知らない場合よりも少ない情報で \(X\) を伝えることができます(”条件付きエントロピー”: \(H(X|Y)\) )。
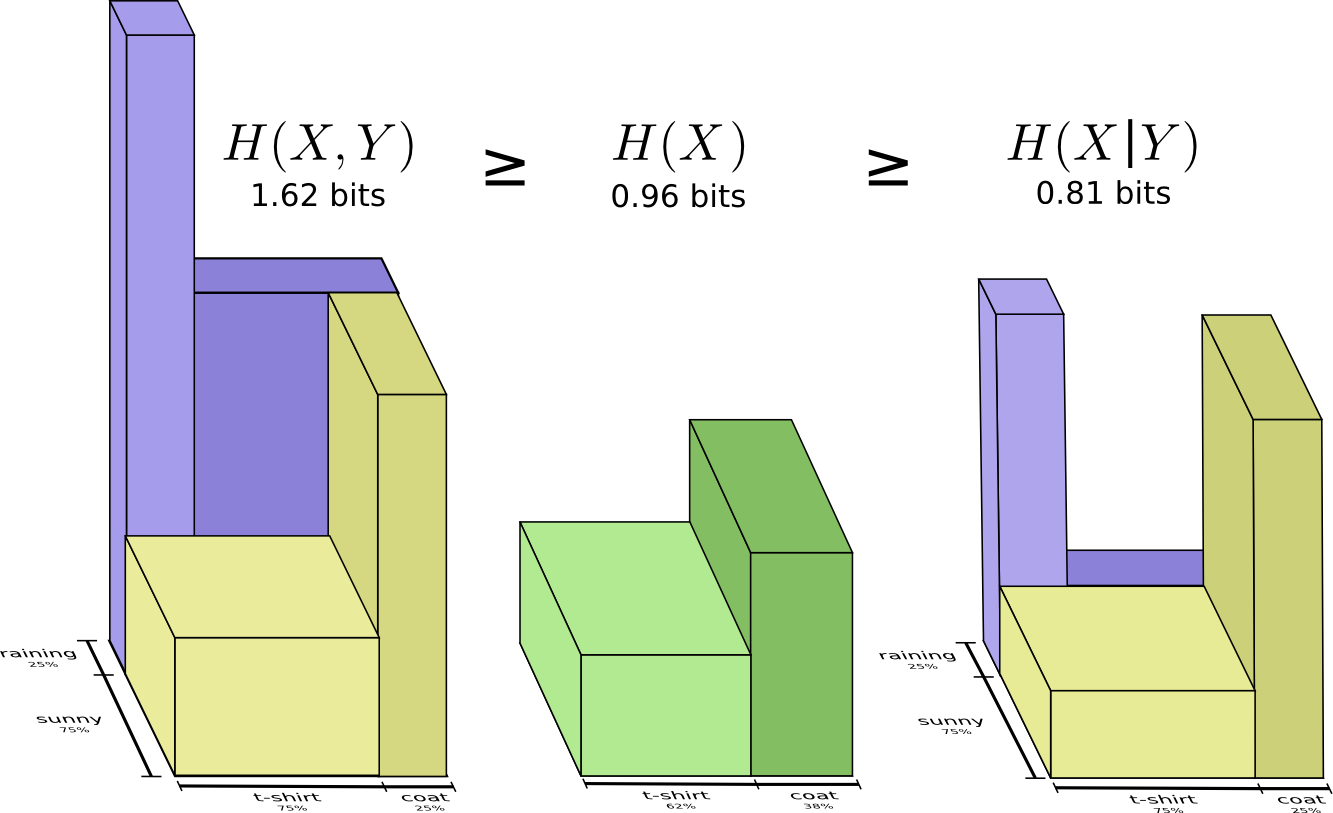
少々複雑に思えるかもしれませんが、帯のイメージで考えるととてもシンプルです。 \(H(X|Y)\) は、既に \(Y\) を知っている誰かに \(X\) を伝える時に送らなければならない情報( \(X\) に含まれる情報のうち、 \(Y\) に含まれない情報)です。視覚的に言えば、 \(H(X|Y)\) は \(H(X)\) 帯のうち \(H(Y)\) と重なり合わない部分です。
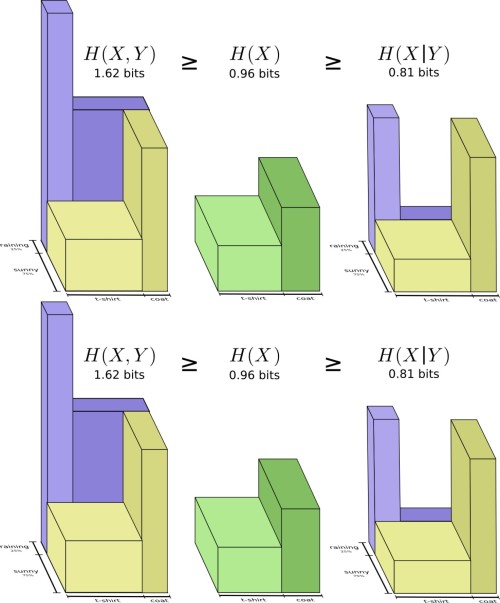
これで、次の図表から不等式 \(H(X,Y) \geq H(X) \geq H(X|Y)\) を読み取ることができるでしょう。
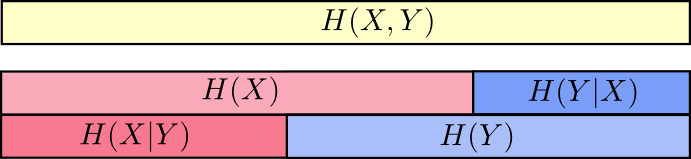
もう1つの式は \(H(X,Y) = H(Y) + H(X|Y)\) です。 \(X\) と \(Y\) の情報は、 \(Y\) の情報に、 \(X\) に含まれているものの \(Y\) には含まれていない情報を加えた和と等しいということです。
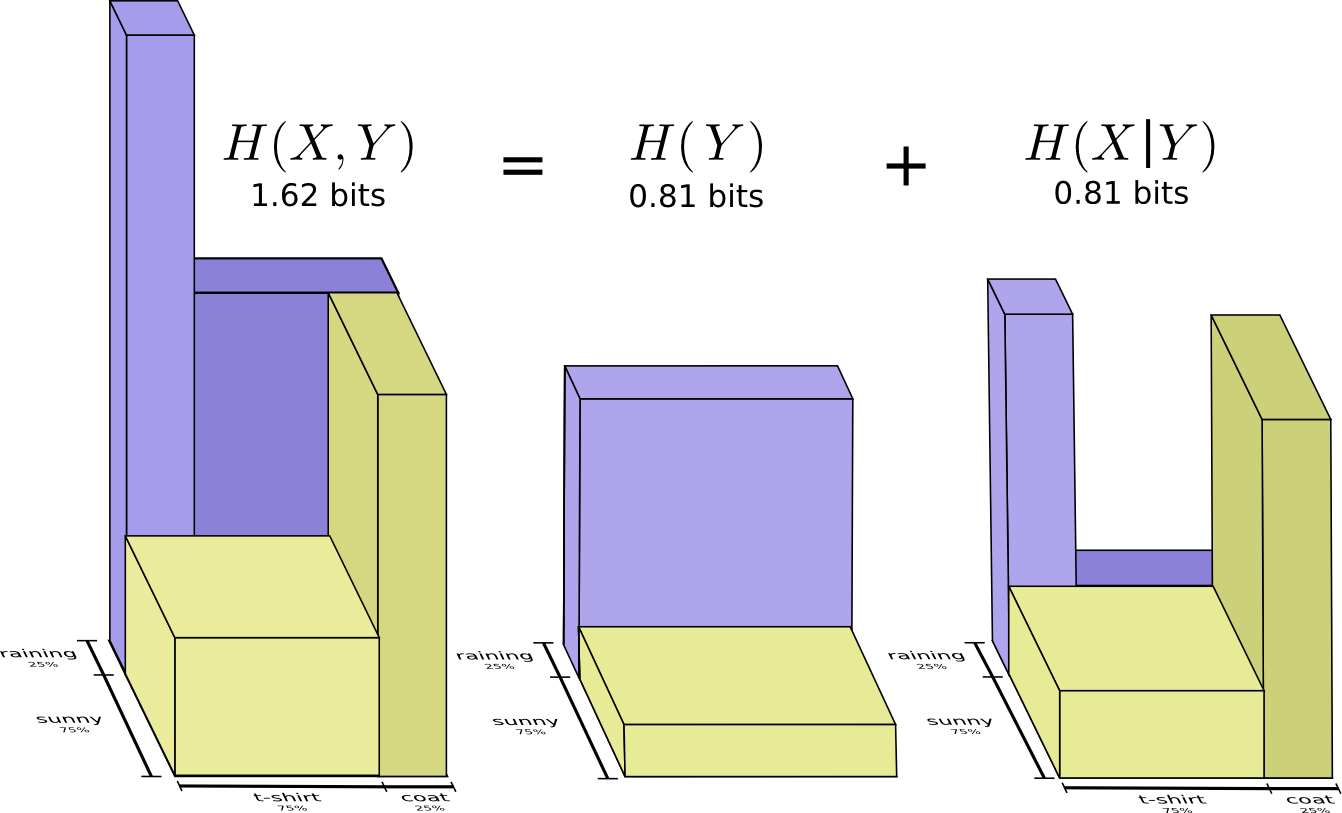
これも、等式で見ると難しいのですが、重なり合う情報の帯として考えれば簡単です。
ここでは、 \(X\) と \(Y\) の情報をいくつかの方法で分割しています。各変数に関する情報 \(H(X)\) と \(H(Y)\) があります。その両方の和集合、 \(H(X,Y)\) があります。片方にあって片方にない情報、 \(H(X|Y)\) と \(H(Y|X)\) も持っています。この多くが、変数間で共通している情報、つまり情報の積集合を中心に展開しているように見えます。この積集合を相互情報量、 \(I(X,Y)\) と呼び、次のように定義し ます。: ^(5)
\[I(X,Y) = H(X) + H(Y) – H(X,Y)\]
この定義が機能するのは、 \(X\) と \(Y\) の両方それぞれに相互情報量が1セットずつ含まれる故に \(H(X) + H(Y)\) には相互情報量が2セット含まれる一方で、 \(H(X,Y)\) には相互情報量が1セットしか含まれないからです(前の帯の図表を思い出してください)。
相互情報量と密接に関わっているのは、情報偏差です。情報偏差は変数間で共有されていない情報です。以下のように定義できるでしょう。 \[V(X,Y) = H(X,Y) – I(X,Y)\]
情報偏差が面白いのは、異なる変数間の測定基準として距離を提供してくれるからです。「1つの変数の値が分かればもう1つの変数の値もわかる」という場合は情報偏差はゼロになり、2つの変数が独立になるにつれて2つの変数間の情報偏差は大きくなります。
これは、同様に距離感を示すKL情報量とどのように関わっているでしょうか。KL情報量で分かるのは、同じ変数や変数の組における2つの分布間の距離です。対して情報偏差は、連帯して分布する2つの変数の間の距離を表します。KL情報量は複数の分布の間の関係であり、情報偏差は1つの分布の中にあるのです。
以上すべてを1つの図表にまとめ、様々な種類の情報の関係性が分かるようにしましょう。
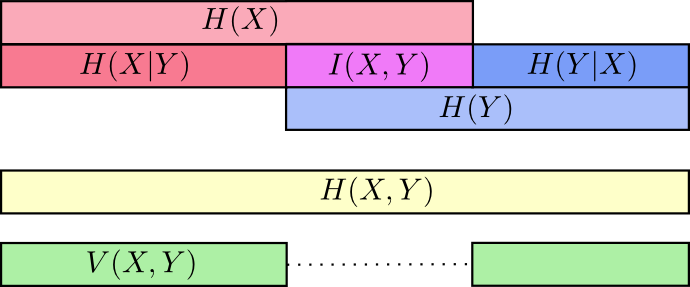
-
この交差エントロピーの表記法は、標準的ではありません。通常の表記は、 \(H(p,q)\) です。この表記法が恐ろしいのには2つの理由があります。1つ目は、結合エントロピーで全く同じ表記が使われることです。2つ目に、交差エントロピーが対称であるように見えることです。これは不合理なので、代わりに私は \(H_q(p)\) と書きます。 ↩
-
この表記法も標準的ではありません。 ↩
-
KL情報量の定義を展開すると次のようになります。: \[D_q(p) = \sum_x p(x)\log_2\left(\frac{p(x)}{q(x)} \right)\] やや風変わりに見えます。どのように解釈すればよいでしょうか。 \(\log_2\left(\frac{p(x)}{q(x)} \right)\) は単に、 \(q\) のために最適化されたコードと \(p\) のために最適化されたコードが、 \(X\) を表す際に使うビット数の差を表しています。式全体としては、2つのコードが使うビット数差の期待値です。 ↩
-
これはRaymond W. Yeungの論文 A New Outlook on Shannon’s Information Measures(シャノンの情報測定に関する新たな考察) で示された一連の情報理論の解釈に基づいています。 ↩
-
相互情報量の定義を展開した場合の式です。 : \[I(X,Y) = \sum_{x,y} p(x,y) \log_2\left(\frac{p(x,y)}{p(x)p(y)} \right)\] どうもKL情報量に似ているようです。どういうことでしょうか。言ってしまえば、これはKL情報量です。P(X,Y) と、そのナイーブな近似であるP(X)P(Y)との間のKL情報量です。つまり、XとYが独立していると仮定するのではなく、 \(X\) と \(Y\) の間の関係性を理解している際に、それらを表現するのに省けるビット数です。これを可視化する気の利いた方法の1つは、文字どおり分布とナイーブな近似の間の比率を絵にすることです。
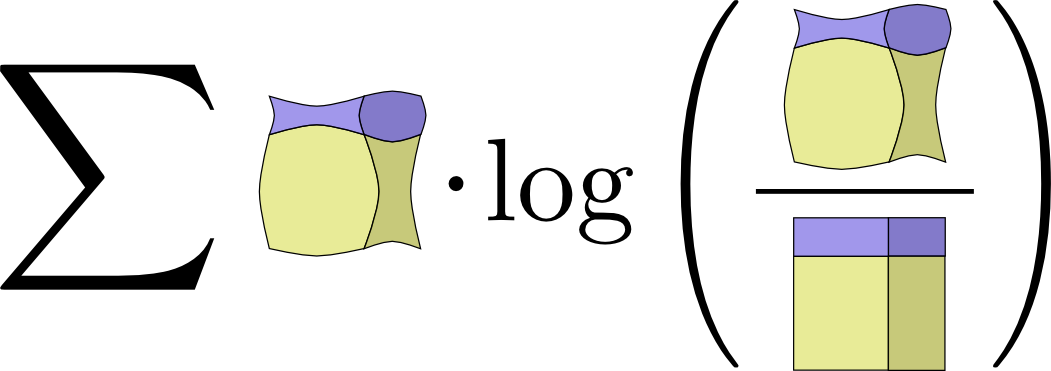 ↩
↩
株式会社リクルート プロダクト統括本部 プロダクト開発統括室 グループマネジャー 株式会社ニジボックス デベロップメント室 室長 Node.js 日本ユーザーグループ代表
- X: @yosuke_furukawa
- Github: yosuke-furukawa

