コードワードの範囲

コードの長さが1ビットなら使用できるコードは0と1の2つ、長さが2ビットなら00、01、10、11の計4つです。つまり1ビット増えるごとに、使用できるコードの数は2倍になります。

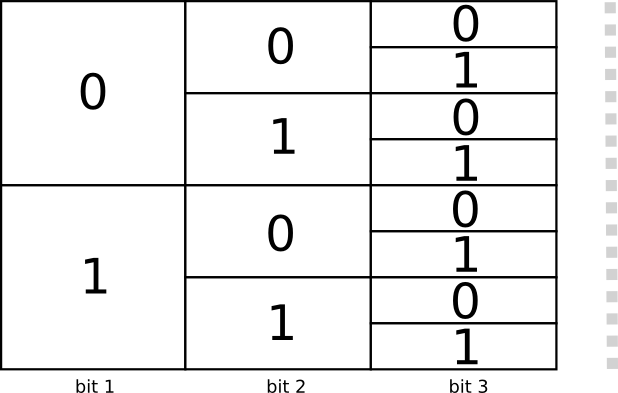
では、コードワードによって長さが異なる可変長コードの場合はどうなるでしょうか。3ビット長のコードワードが8つという単純なケースだけでなく、2ビット長のコードワードが2つと3ビット長のコードワードが4つなど、より複雑な組み合わせも考えられます。このような長さの異なるコードワードをいくつ使用できるかは、何を基に決まるのでしょうか。

前述のとおり、Bobは各単語をコードワードに置き換えて、それらを連結することで、メッセージをエンコードされた文字列に変換しています。

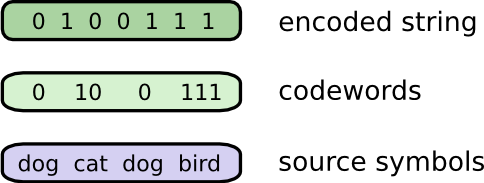
注釈：
エンコードされた文字列
コードワード
元のシンボル

可変長コードを作成する際は、少々厄介な問題があるため注意が必要です。具体的には、エンコードされた文字列を分割してコードワードに戻す方法です。コードワードの長さが一律であれば、単純に文字列を等間隔で分割すれば済みます。しかし、さまざまな長さのコードワードが混在する場合は、その中身についても考慮しなくてはなりません。

ここでの目標は、単一の方法で文字列をデコードし、各コードが一意的にデコードされるようにすることです。エンコードされた文字列に含まれるコードワードが一意に決まらない状態は避ける必要があります。この課題は、「コードワードの区切り」を表す符号を使えば、簡単に解決できるでしょう。 ^(1) しかし、今回はこの方法を取らず、0と1のみを送信します。そのため、連結されたコードワードを調べて、各コードワードの区切りを見極める方法が必要になります。

作成したコードが一意的にデコードできないケースは非常に多くあります。たとえば0と01がともにコードワードだとしましょう。この場合、エンコードされた文字列0100111の最初のコードワードを特定することはできません。0の場合も、01の場合もあり得ます。よって、「ある特定のコードワードに対して、それを長くしたバージョンのコードワードが存在してはならない」という性質が必要になります。言い換えると、どのコードワードも、他のコードワードの接頭部であってはならないということです。この性質は語頭属性と呼ばれ、これを満たすコードを接頭コードと言います。

「あるコードワードを使用することで、ある範囲のコードワードが使用できなくなる」と考えると分かりやすいでしょう。例えば01というコードワードを使う場合、これを接頭部に持つコードワードは使えなくなります。010や011010110などは、どのコードワードなのか一意に定まらないため使用できなくなるのです。

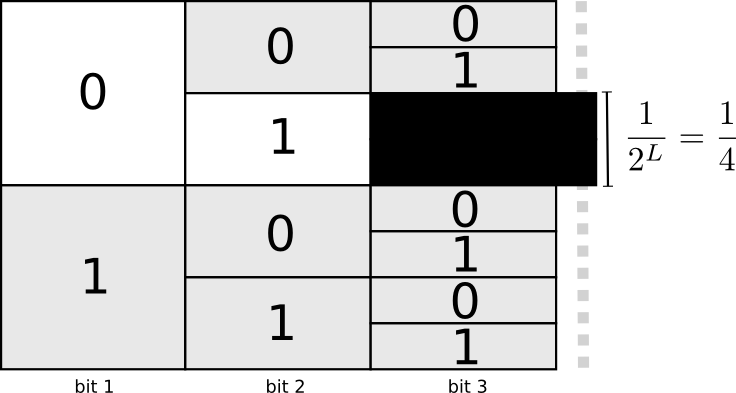
コードワード全体の4分の1は01から始まるため、4分の1のコードワードは使用できなくなります。2ビット長の短いコードワードを1つ使うためには、こうした代償を払わなくてはならず、結果的に他のコードワードを少し長くする必要が生じます。さまざまな長さのコードワードを使用する場合は、この種のトレードオフが常に存在します。あるコードワードを短くすると、使用できるコードワードの範囲が狭まり、他のコードワードを短くできなくなるのです。よって、適当なトレードオフを見極めることが重要になります。

エンコードの最適化

この内容については、限られた予算で短いコードワードを入手すると考えてみるとよいでしょう。1つのコードワードを得るには、そのコストとして一部のコードワードを犠牲にしなくてはなりません。

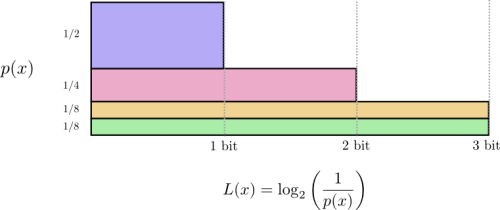
長さが0のコードワードのコストは1で、これは利用可能な全てのコードワードになります。つまり、コードワードの長さが0だと、他のコードは使用できません。次に、長さが1のコードワード「0」の場合は、取り得るコードワードの1/2は「0」から始まるため、コストは1/2になります。同様に長さが2のコードワード「01」の場合は、取り得るコードワードの1/4は「01」から始まるため、コストは1/4です。まとめると、コードワードのコストは、コードワードの長さが増すにつれて 指数関数的に 減少します。

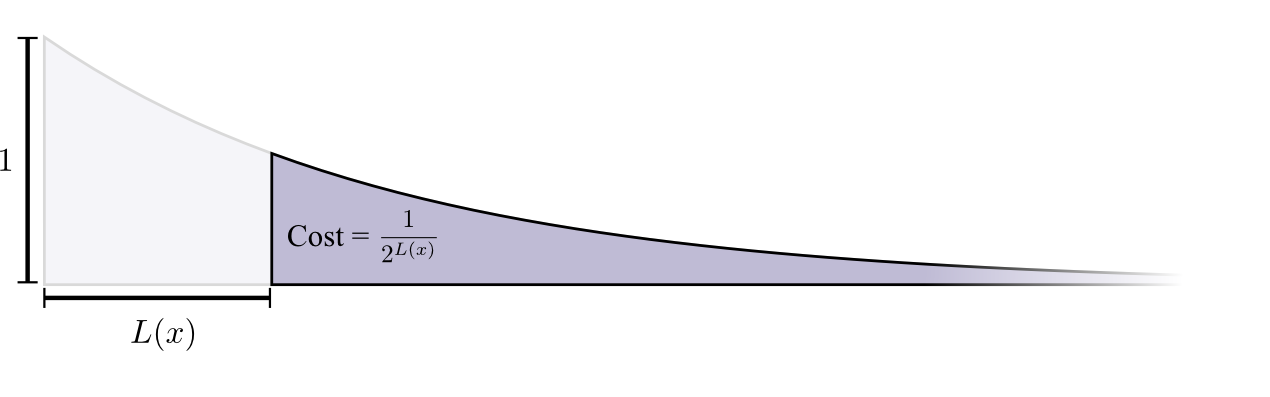
上のように、コストが（自然対数を底とする）指数関数的に減少する場合、それは高さと面積の両方に当てはまる点に注目してください。 ^(2)

では、メッセージ長の平均値を短くするために、コードワードを短くしましょう。各コードワードを使用すると、メッセージ長の平均値は「そのコードワードの発生確率×コードワード長」倍だけ長くなります。例えば発生確率が50％の4ビット長のコードワードを送信する場合は、このコードワードを送信しない場合に比べて、メッセージ長の平均値は2ビットだけ長くなります。図にすると以下の長方形のようになります。

注釈：
メッセージ長の平均値の増分

コードワードのコストとメッセージ長の平均値は、コードワード長で関連付けられています。つまり、投じるコストによってコードワード長が決まり、コードワード長によってメッセージ長の平均値の増分が決まります。これらをまとめて図示すると以下のようになります。

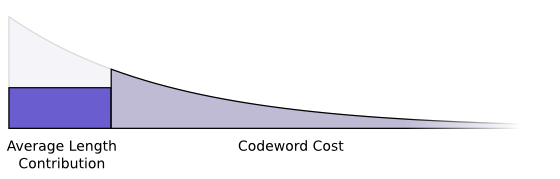
注釈：
メッセージ長の平均値の増分
コードワードのコスト

コードワードが短くなると平均のメッセージ長も短くなりますが、コストがかさみます。逆にコードワードが長くなると平均のメッセージ長も長くなりますが、コストは抑えられます。

注釈：
コードワードが短く、コストが高い
コードワードが長く、コストが低い

では限られたコストを有効に使うにはどうしたらよいのでしょうか？　各イベントで、どれだけの予算をコードワードに費やすべきかを考えてみましょう。

使用頻度の高いツールに投資するように、発生頻度の高いコードワードに予算をかけたいと思うのは、ごく自然なことです。つまりイベントの発生頻度に比例して、予算を割り当てます。例えば発生頻度が50％のイベントには、予算の50％を割いて短いコードワードを得ます。一方で発生頻度が1％のイベントには、予算の1％しか割り当てません。使用頻度の低いコードワードは、長くてもそれほど気にする必要がないからです。

これは実に自然な方法に思えますが、本当に最善策なのでしょうか？　答えはイエスです。それをこれから証明しましょう。

以下の証明は、画像を使用して分かりやすく説明していますが、この記事で一番難しい部分なので、理解するのに苦労するかもしれません。よって、この内容と前提として受け入れて、次のセクションに飛んでいただいても構いません。

では具体例として、2つのイベントが発生する会話について考えてみましょう。イベント \(a\) の発生する頻度を \(p(a)\) 、イベント \(b\) の発生する頻度を \(p(b)\) とします。予算は上記の自然な方法で割り当てます。コードワード \(a\) を短くするために予算の \(p(a)\) 割を、コードワード \(b\) を短くするために予算の \(p(b)\) 割を費やします。

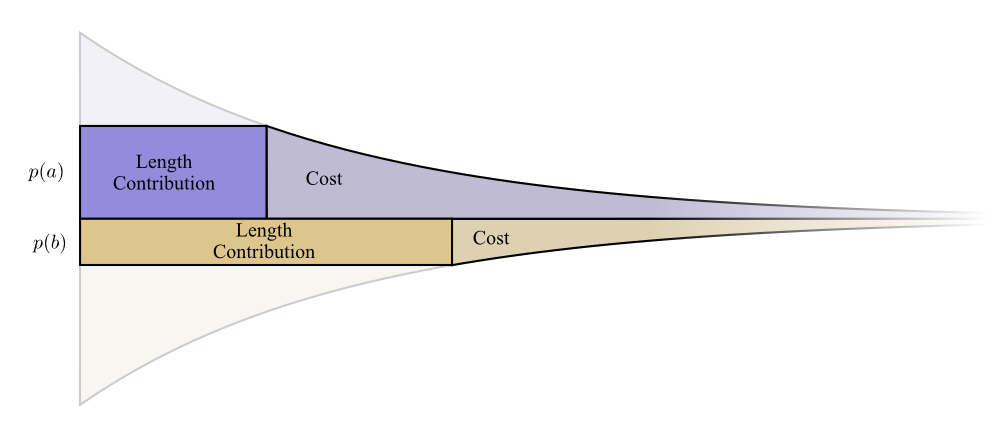
注釈：
長さの増加分
コスト

ここでは、コストと長さの増分の境界はピッタリとそろっています。これは何を意味するのでしょうか？

まず、コードワードの長さをわずかに変えた時の、コストと長さの増分への影響を見てみましょう。コードワードを少しだけ長くすると、メッセージ長の増分は境界の高さに比例して増加します。一方でコストは境界の高さに比例して減少します。

コードワード \(a\) を短くするためのコストは \(p(a)\) です。この時、各コードワードの長さはどれも同等に重要なわけではなく、重要度はそれぞれの使用量に比例します。 \(a\) を使用する割合は \(p(a)\) なので、 \(a\) のコードワードを少し短くする利益は \(p(a)\) ということになります。

興味深いことに、同じ値が導かれました。つまり元々の予算には面白い性質があって、よりコストをかけるほど、その投資額に応じてコードワードを短くしたことによる利益が得られるのです。つまり、コストに対する利益の比を考慮して、より多く投資する対象を決めればよいということです。ここでは、その比は \(\frac{p(a)}{p(a)}\) なので1になります。 \(p(a)\) の値によらず、常に1です。同じことが、もう1つのイベントについても言えます。利益/コストの値は常に1なので、どのコードワードへの投資を少し増やしても同じ価値があるということになります。

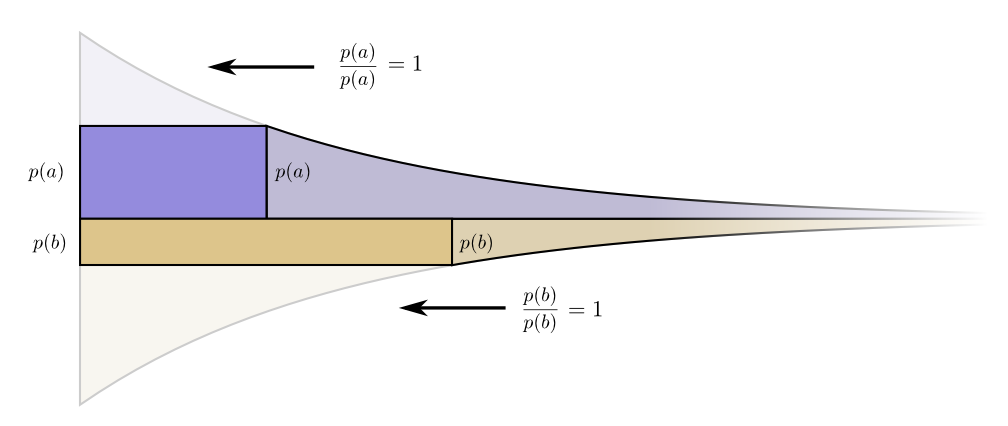
ごくわずかであれば、予算を変えても意味がないと言えます。しかし、これだけでは最適な予算だという証明にはなりません。では証明をするために、一方のコードワードの予算の一部を他方のコードワードに当てる予算パターンを考えましょう。 \(b\) の予算をε減らして、その分を \(a\) に当てます。これにより \(a\) のコードワードが少し短くなり、 \(b\) のコードワードが少し長くなります。

ここでは、より短い \(a\) のコードワードを買うコストは \(p(a) + \epsilon\) 、より短い \(b\) のコードワードを買うコストは \(b\) になります。しかし利益は変わりません。よって、 \(a\) のコストに対する利益の比は \(\frac{p(a)}{p(a) + \epsilon}\) となり、1よりも小さくなります。一方で \(b\) のコストに対する利益の比は \(\frac{p(b)}{p(b) – \epsilon}\) となり、1よりも大きくなります。

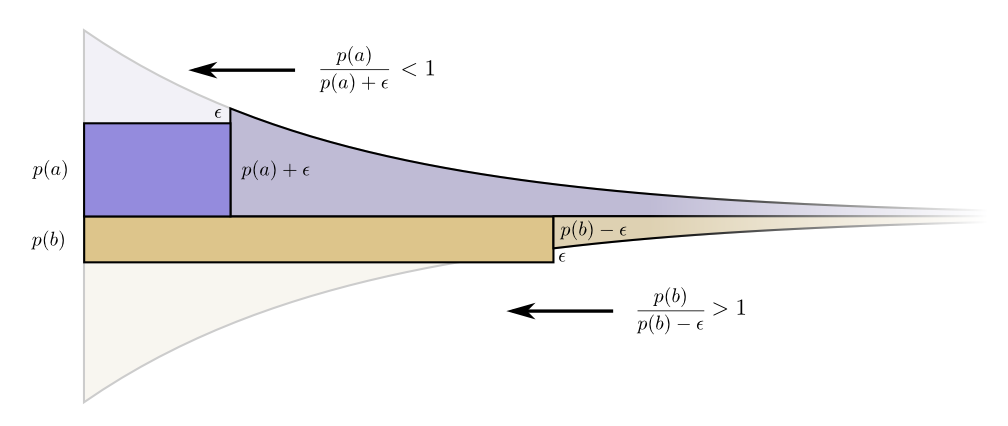
そうなると価格の均衡は崩れ、 \(a\) よりも \(b\) の方がお得になります。投資家は「 \(b\) を買え、 \(a\) を売れ」と言うでしょう。実際にそのようにすると、元の予算案に戻るわけです。つまり、元々の予算案に近づけることで、全体的な予算案が改善されるのです。

元々の「各コードワードには使用頻度に比例した額を投資する」という予算案は、自然であるだけなく、最適な方法だったのです（上記の証明は2つのコードワードに限定されるものですが、より多くのコードワードに対応するよう簡単に一般化することができます）。

（注意深い読者の方は、最適な予算によって決まるコードで、コードワードの長さが小数になる可能性があることに気づいたかもしれません。そうなると、非常に厄介な状況になります。一体どういうことでしょうか？　現実的には、1つのコードワードを送信して通信をしたい場合は、当然ながら整数に丸める必要があります。しかし後述のように、一度に多くの情報を送る場合は、実は小数のコードワードを送ることができます。これについては後ほど説明しますので、そちらをご覧ください。）

エントロピーの計算

前述のとおり、長さが \(L\) のメッセージのコストは \(\frac{1}{2^L}\) です。この関係から、逆にコストが分かれば \(\log_2\left(\frac{1}{\text{cost}}\right)\) を計算することで、メッセージ長を求めることができます。 \(x\) のコードワードに使うコストは \(p(x)\) だったので、長さは \(\log_2\left(\frac{1}{p(x)}\right)\) になります。この値が採用すべき最適な長さです。

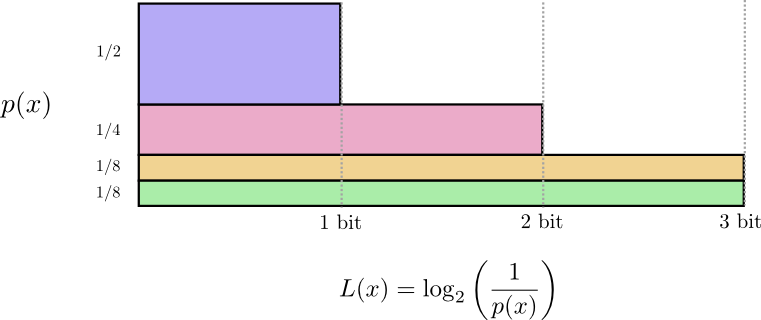
先ほど議論したように、イベントを送受信するための平均メッセージ長をどこまで短くできるかは、本質的に確率分布 \(p\) によって決まります。最適なコードを使った際の平均メッセージ長の下限をpのエントロピーと言い、 \(p\) , \(H(p)\) と表します。すでにコードワードの最適な長さは分かっているので、以下の式でエントロピーを計算できます。
\[H(p) = \sum_x p(x)\log_2\left(\frac{1}{p(x)}\right)\]
一般的には、 \(\log(1/a) = -\log(a)\) という関係を使って、 \(H(p) = – \sum p(x)\log_2(p(x))\) と表現します。個人的には前者の方が感覚的に分かりやすいと思うので、この記事ではそちらを使います。）

いずれにせよ、イベント発生時に通信を行うには、最低でもこのビット数を送信しなければなりません。

何かを伝達する際に必要な平均情報量により、明確に圧縮方法が示唆されます。それ以外にも平均情報量について考慮すべき理由はあります。平均情報量は不確定度合い表すとともに、情報を定量化する方法を与えてくれるのです。

何が起こるか分かっていたら、メッセージを送る必要はありません。また、それぞれ50％の確率で発生する2つの事象があれば、1ビットを送るだけで済みます。しかし64個の事象が等しい確率で発生し得る場合は、6ビットを送信しなければなりません。発生確率が高いほど、平均メッセージ長が短く、より優れたコードを作成できます。一方、発生確率が低いほど、メッセージを長くせざるを得なくなります。

一般的に結果が不確かであるほど、何が起きたか判明した時に学ぶことは多いものです。