新しいニューラルネットワークのアーキテクチャがその時々で誕生するため、それら全部を把握することは困難です。全ての略語を覚えようとすると、最初はその数の多さに圧倒されてしまうでしょう（DCIGNやBiLSTM、DCGANを知っている人はいますか？）。

そんなわけで、これらのアーキテクチャの多くを盛り込んだチートシートを作ることにしました。そのほとんどはニューラルネットワークです。しかし、中には全く異なるアーキテクチャも潜んでいます。どれも独特で目新しいアーキテクチャばかりですが、ノードの構造を描くことで基本的な関係が分かりやすくなってきます。

これらをノードマップとして描くことの問題点は、これらがどのように使われるかを明確に示していないという点です。例えば、変分オートエンコーダ（VAE）はオートエンコーダ（AE）と同じように見えますが、実際は訓練過程が全く異なりますし、訓練したネットワークのユースケースは更に大きく異なっています。というのも、VAEは、ノイズを挿入することで新しいサンプルを得るジェネレータなのです。AEは、あらゆる入力を、”記憶している”訓練サンプルのうち最も近いものに単純にマッピングします。この概要では、異なるタイプのノードが内部でどのように働くかを全く明らかにしていないということも補足しておきましょう（別の機会に取り上げます）。

使用されている略語は、そのほとんどが一般的に認められていますが、全てではないということも言及しておきます。RNNは再帰型ニューラルネットワーク（Recursive Neural Network）の略語として使われることもありますが、ほとんどの場合は回帰結合型ニューラルネットワーク（Recurrent Neural Network）を示します。それだけではなく、LSTMやGRU、そして双方向性タイプまで含む、あらゆる再帰的なアーキテクチャのプレースホルダとしてRNNは使われます。AEも似たような問題を抱えていて、VAEやDAE、その他の類似のネットワークが単純にAEと呼ばれることがあります。また、語尾に加える”N”の数によって多くの略語が変化します。なぜなら、畳み込みニューラルネットワーク（Convolutional Neural Network）とも、単純に畳み込みネットワーク（Convolutional Network）とも呼べるからです（結果として、CNNと略されたりCNと略されたりします）。

常に新しいアーキテクチャが開発されているため、完璧なリストを作るのは実質的に不可能です。公開されたアーキテクチャを探しているとしても、それを見つけるのは非常に困難ですし、時には見落としてしまうこともあります。このリストでAIの世界を見渡せますが、執筆後、しばらく経ってから本稿を読んだ場合は、全てがリストに包括されているとは思わないでください。

それぞれのアーキテクチャを図にし、 非常に 短い説明を加えています。よく知っているアーキテクチャが幾つかあっても、あるアーキテクチャについては分からないといった場合に、この図が役に立つでしょう。

---

順伝播型ニューラルネットワーク（Feed forward neural networks, FF or FFNN）とパーセプトロン（P） は単一方向にだけ進むネットワークです。情報は前から後ろへと送られていきます（入力から出力へと伝播されます）。ニューラルネットワークには層があると説明されることが多く、それぞれの層が入力、隠れ、または出力というセルで構成され平行に並んでいます。単独の層内で接続することはなく、通常は隣り合った層同士で完全接続します（ある層の中に含まれる全てのニューロンが、別の層の各ニューロンと接続します）。実際に、最も単純なネットワークは、2つの入力セルと1つの出力セルを持っており、論理ゲートの形成に使うことができます。FFNNの訓練は、”何を入力するのか”と”何を出力したいのか”がペアになったデータセットを与え、バックプロパゲーションで行うのが一般的です。これは教師あり学習と呼ばれ、入力値だけを与えてネットワークに出力させる教師なし学習とは相反する手法です。多くの場合、逆伝播させる誤差としては、入力と出力の偏差のバリエーション（例えば平均二乗誤差や、単純な線形差分など）が用いられます。ネットワークに十分な数の隠れニューロンがあれば、理論的には常に、ネットワーク上で入力と出力の間の接続が形成されていることになります。このネットワーク自体が実用できるケースははかなり限られていますが、他のネットワークとの組み合わせによって新しいネットワークを作るのによく用いられます。

Rosenblatt, Frank. “The perceptron: a probabilistic model for information storage and organization in the brain.” Psychological review 65.6 (1958): 386.
原文PDF

---

放射基底関数（Radial basis function, RBF） ネットワークは、放射基底関数を活性化関数として使うFFNNのことです。それ以上の説明はありません。使われないからというわけではありませんが、他の活性化関数を使ったFFNNに決まった名称があるものはほとんどありません。これは、状況に合わせてネットワークを作るということが大きく関係しています。

Broomhead, David S., and David Lowe. Radial basis functions, multi-variable functional interpolation and adaptive networks. No. RSRE-MEMO-4148. ROYAL SIGNALS AND RADAR ESTABLISHMENT MALVERN (UNITED KINGDOM), 1988.
原文PDF

---

ホップフィールドネットワーク（Hopfield network:HN） は、どのニューロンも他の全てのニューロンに接続しているようなネットワークです。つまり、まるで完全に絡みあった状態で皿に盛りつけられたスパゲッティのようなもので、もっというと全てのノードが全ての役割として機能するのです。各ノードは、訓練前は入力、訓練中は隠れ、訓練後は出力となります。ニューロンの値を望ましいパターンにセットすることでネットワークは訓練され、その後重みが計算されます。それ以降、重みは変わりません。いったん1つ以上のパターンの訓練を受ければ、ネットワークは常に学習したパターンの中の1つに収束します。なぜならネットワークはそれらの状態でのみ安定であるからです。しかし、それが必ずしも望ましい状態と一致しているわけではないということにご注意ください。（残念ながら魔法のブラックボックスではありません）。訓練の間、ネットワークの”エネルギー”あるいは”温度”の総計が徐々に減少することにより状態はある程度安定します。各ニューロンはこの温度に比例する活性化の閾値を持ちます。そして、入力を足し合わせることによって閾値を超えると、入力はニューロンが2つの状態（通常は-1か1、場合によっては0か1）のどちらか1つの状態をとることになります。ネットワークの更新は同期的に行われるか、より一般的には1つずつ順次的に行われます。1つずつ更新する場合には、公正なランダムシーケンスが作られ、「どのセルがどういう順序で更新されるか」がそのシーケンスによって構成されます。（「公正なランダムシーケンス」とは、各nアイテムで全ての選択(n)がきちんと1回起こるということです）。これにより、「全てのセルが更新されたがどれも変化しなかった場合、ネットワークは安定している(焼きなまされ終わっている)」ということになるので、ネットワークが安定（収束）したかどうかがわかるのです。このネットワークはよく連想記憶と呼ばれます。それは、入力値に最も似ている状態に出力値が収束するからです。人が半分のテーブルを見て残りの半分を想像できるのであれば、このネットワークは「半分がノイズで半分がテーブル」の入力値が与えられるとテーブルに収束するでしょう。

Hopfield, John J. “Neural networks and physical systems with emergent collective computational abilities.” Proceedings of the national academy of sciences 79.8 (1982): 2554-2558.
原文PDF

---

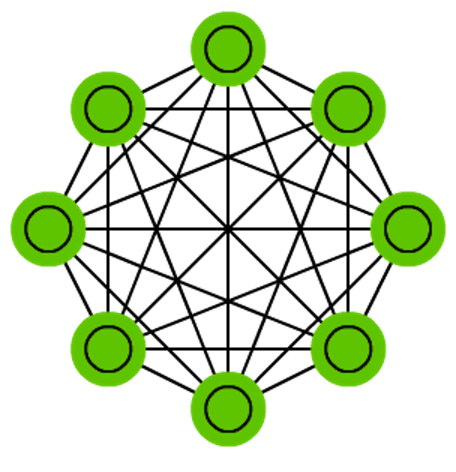
マルコフ連鎖(Markov chains: MC, あるいは離散時間マルコフ連鎖:discrete time Markov Chain (DTMC)) はBMとHNの前身のようなものです。MCは、「現在のノードから、隣接ノードのいずれかに向かう確率は？」として考える事ができます。ノードは記憶を持たず（これをマルコフ性と言います）、このことは「最終的な状態が直前の状態に完全に依存する」ということを意味します。実際にはニューラルネットワークではないのに、ニューラルネットワークに実によく似ていて、BMやHNの理論的な基礎を形成します。MCは、必ずしもニューラルネットワークとは考えられていません。またBMやRBM、HNもニューラルネットワークと考えられていません。これらと同様、マルコフ連鎖は必ずしも完全接続ではありません。

Hayes, Brian. “First links in the Markov chain.” American Scientist 101.2 (2013): 252.
原文PDF

---

ボルツマンマシン（BM） はHNにとてもよく似ています。ですが、幾つかのニューロンが入力ニューロンとされ、他のニューロンは”隠れ”のままです。ネットワーク全体の更新の最後に、入力ニューロンは出力ニューロンに変わります。BMはまずランダムな重み付けの状態から始まり、バックプロパゲーションを通して、またごく最近ではコントラスティブ・ダイバージェンスを通して学習します（マルコフ連鎖は2つの情報ゲイン間の勾配を決定するのに用いられます）。HNと比較すると、大部分のニューロンは2値のアクティベーションパターンを持っています。MCによって訓練されていると示唆したように、BMは確率論的ネットワークです。BMの訓練と実行プロセスはHNとかなり類似しています。入力ニューロンをある固定値にセットし、その後ネットワークを開放します（その影響は受けません）。解放中は、セルはどんな値も取ることができ、また入力ニューロンと隠れニューロンの間を繰り返し行ったり来たりします。アクティベーションはグローバルな温度の値によってコントロールされ、温度が下がれば、セルのエネルギーも下がります。こうして生じる低いエネルギーによりアクティベーションパターンは安定します。ネットワークは、適切な温度で平衡に達します。

Hinton, Geoffrey E., and Terrence J. Sejnowski. “Learning and releaming in Boltzmann machines.” Parallel distributed processing: Explorations in the microstructure of cognition 1 (1986): 282-317.
原文PDF

---

制限付きボルツマンマシン（RBM） は名前のとおり著しくBMに類似しており、従ってHNにも類似しています。BMとRBMの最大の違いは、「RBMの方が制約が多いため使いやすい」ということです。個々のニューロンの適切な接続を誘発するのではなく、異なるニューロンのグループと他の全てのニューロンのグループの接続だけを実行し、入力ニューロン同士の直接接続や隠れニューロン同士の接続は実行しません。ひねりを効かせれば、FFNNのようにRBMを訓練することができます。つまり、データを前方向に渡したあとバックプロパゲーションを行うのではなく、データを前方向に渡したのち後方向にデータを渡します（前の層に戻します）。その後は、順伝播法とバックプロパゲーションを使用して訓練することができます。

Smolensky, Paul. Information processing in dynamical systems: Foundations of harmony theory. No. CU-CS-321-86. COLORADO UNIV AT BOULDER DEPT OF COMPUTER SCIENCE, 1986.
原文PDF

---

オートエンコーダ（AE） は、FFNNにいくらか類似しています。根本的なアーキテクチャに違いがあるのではなく、FFNNの使用方法が異なるのです。AEの基本的な考え方はその名のとおり、自動的に情報をエンコードすることにあります（この場合、暗号化という意味ではなく、圧縮という意味です）。ネットワークは砂時計の形をしていて、隠れ層は入出力層よりも小さくなっています。また、中間層について常に対称となっています(全体の層数が偶数なら中間層は2層、奇数なら1層になります)。ほとんどの場合、最も小さな層が中間層であり、そこでは情報が最も圧縮されています（ネットワークのチェックポイントとなります）。真中までの部分をエンコード部分、真中以降をデコード部分、真中をコード部分とします。入力を与え、入力と出力の差分を誤差としてバックプロパゲーションを行うことで訓練できます。AEは重みに関しても対称的な構築が可能なため、エンコードとデコードの重みを等しくすることができます。

Bourlard, Hervé, and Yves Kamp. “Auto-association by multilayer perceptrons and singular value decomposition.” Biological cybernetics 59.4-5 (1988): 291-294.
原文PDF

---

スパース・オートエンコーダ（SAE） はある意味AEの反対になります。多くの情報をより狭い”空間”やノードで表現するようネットワークに学習させるのではなく、より多くの空間に情報をエンコードさせるのです。そのため、ネットワークを「中間層で収束させ、その後入力した時のサイズに戻す」という形にせず、中間層を大きくします。このタイプのネットワークは、1つのデータセットから多くの特徴を抽出するのに使えます。SAEをAEと同じ方法で訓練すると、ほとんどの場合において役に立たない恒等ネットワーク（つまり、入力されたものは変換や分解されずにそのままの形で出力されるだけ）ができてしまいます。これを回避するためには、入力をフィードバックするのではなく、入力にスパーシティドライバを足したものをフィードバックします。このスパーシティドライバは閾値フィルタの形をとり、ある特定の誤差のみが戻されて学習の対象となり、その他の誤差は逆伝播について”無関係”とされ、ゼロに設定されます。これは全てのニューロンが常に必ずしも常に発火している状態ではない（そして、ポイントは発火が生物学的に妥当かどうかになります）、スパイキングニューラルネットワークであることを表しています。

Marc’Aurelio Ranzato, Christopher Poultney, Sumit Chopra, and Yann LeCun. “Efficient learning of sparse representations with an energy-based model.” Proceedings of NIPS. 2007.
原文PDF

---

変分オートエンコーダ（VAE） はAEと同じアーキテクチャをしていますが、異なることを”教え”られます。それは、入力されたサンプルの確率分布の近似です。BMやRBMに緊密に関係しているため、根本に少し立ち返るようなものになります。しかし、VAEは異なる表現を達成するための確率的推論や独立性に関するベイズ統計学、再パラメータ化のトリックをベイズ確率に頼っています。推論や独立の部分は直感的に理解できるものの、複雑な数学理論に依存しています。基本を要約すると、「影響を考慮せよ」ということです。ある事象がある場所で発生し、別の事象が別の場所で発生した場合、必ずしも2つの事象に関連性があるとは限りません。関連性がない場合は、誤差伝播はそのことを考慮します。ニューラルネットワークは大きなグラフとも言えるため、深層に進みながらあるノードから別のノードに与える影響を除外することができます。

Kingma, Diederik P., and Max Welling. “Auto-encoding variational bayes.” arXiv preprint arXiv:1312.6114 (2013).
原文PDF

---

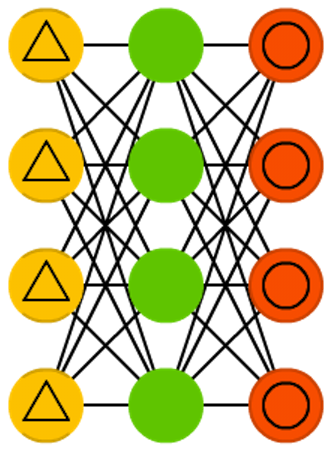
デノイジング・オートエンコーダ（DAE） はデータを入力するだけでなく、入力するデータにノイズを付けて（例えば画像を荒くします）用いるAEです。誤差の算出する場合には同じ手法を使います。つまり、ネットワークからの出力とノイズなしの元の入力データを比較します。ノイズによって常に小さな特徴が変化し続けることから、小さな特徴を学習することが”間違い”となり、コンピュータは細かい特徴でなく大きな特徴を学習するようになります。

Vincent, Pascal, et al. “Extracting and composing robust features with denoising autoencoders.” Proceedings of the 25th international conference on Machine learning. ACM, 2008.
原文PDF

---

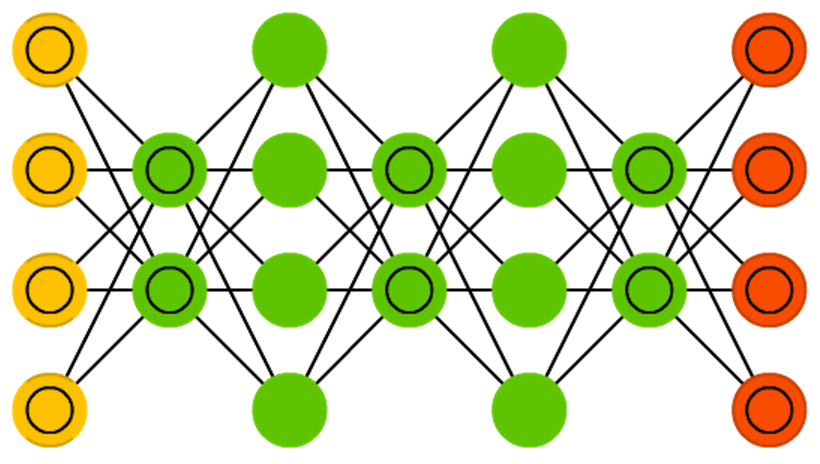
ディープビリーフネットワーク（DBN） はRBMやVAEをスタックした(積み重ねた)アーキテクチャを指します。AEやRBMが前のネットワークをエンコードすることだけを学習するのに対し、DBNはスタックごとに効率よく訓練できることが確認されています。このテクニックはGreedy trainingとしても知られていますが、ここでの”Greedy(貪欲)”は、「『最適ではないかもしれないがまともな解』を得るために局所最適解を作り出す」ということを意味します。RBMやVAE同様にDBNも、コントラスティブ・ダイバージェンスやバックプロパゲーションを通して学習することで、データを確率的モデルとして表現することができるようになります。ひとたび訓練されるか教師なし学習で（より）安定した状態に収束すれば、モデルを使用して新しいデータを生成することができるようになります。コントラスティブ・ダイバージェンスで訓練すれば、異なる特徴を探すことを学習するため、既存のデータを分類することもできます。

Bengio, Yoshua, et al. “Greedy layer-wise training of deep networks.” Advances in neural information processing systems 19 (2007): 153.
原文PDF

---

畳み込みニューラルネットワーク(CNN,または深層畳み込みニューラルネットワーク(DCNN)) は、他のネットワークとはかなり異なります。主に画像処理に使用されますが、音声などの入力にも使用することができます。典型的なCNNの使用例は、ネットワークに画像を入力し、入力されたデータをネットワークに分類させることが挙げられます。例えば、猫の画像を入力したら、”猫”が出力され、犬の画像を入力したら”犬”を出力します。CNNの最初の部分は主に入力”スキャナ”となりますが、これは訓練データを一度に解析することを意図していません。例えば200×200ピクセルの画像を入力するのに、40,000ノードある層を使いたくはありませんね。その代わり、例えば20×20をスキャンできる入力層を作成し、20×20ピクセル分の画像を入力します（大抵の場合、画像の左上端から始めます）。入力を渡したら(学習に使う場合も使えるはずです)、右に1ピクセル分移動し、次の20×20ピクセル分の画像を入力します。20ピクセル分（あるいはスキャナ分）移動するのではなく、画像を20×20の塊に分解しているのでもなく、画像の上をクロールしていることにご注意ください。この入力データは、通常の層の代わりに全てのノードが全て接続されている畳み込み層を介してフィードされます。各ノードは近くのセル（近さは実装によって異なりますが、大抵の場合は数ピクセル分）のみを問題とします。深くなるにつれこの畳み込み層は小さくなりますが、多くの場合、入力を簡単に割り切れる因数で割っていきます（つまり、20は10の層、さらに5の層になります）。ここで非常によく用いられるのが2のべき乗(32、16、8、4、2、1)なのですが、これはきれいにそして完全に割り切れるためです。CNNは畳み込み層以外にプーリング層を持っています。プーリングは詳細をフィルタリングする方法なのですが、一般的に使用されるプーリングの手法はマックスプーリングと呼ばれ、例えば2×2ピクセルのピクセルを入力にとり、最も大きな値を渡します。CNNを音声に適用する場合、オーディオ音波を少しずつ音声クリップ長ごとのセグメントで入力していきます。実際のCNNの実装においては、データをさらに処理するため、最後にFFNNが貼付けられています。これにより、非線形の抽象化が可能になります。このようなネットワークをDCNNと呼んでいますが、必ずしもCNNと明確に区別して使用されている訳ではなく、しばしば同じものとして使用されます。

LeCun, Yann, et al. “Gradient-based learning applied to document recognition.” Proceedings of the IEEE 86.11 (1998): 2278-2324.
原文PDF