素数か2のべき乗か

ハッシュテーブルのアイテムをルックアップする際に高負荷なステップが3つあります。

1. キーをハッシングする
2. キーをスロットにマッピングする
3. 該当スロットのメモリをフェッチする

ステップ1は、キーが整数であれば、低負荷になります。単にintをsize_tにキャストするだけです。しかし、文字列のようなタイプのキーの場合は高負荷となります。

ステップ2はよくある整数モジュロ演算です。

ステップ3はポインタの間接参照です。std::unordered_mapの場合は複数のポインタ間接参照となります。

処理の遅いハッシュ関数でなければ、直観的にステップ3が最も高負荷になると考えると思います。しかし、全てのルックアップでキャッシュミスが生じなければ、整数モジュロが最も高負荷な処理となります。現代のハードウェアにおいても整数モジュロは非常に遅いのです。 Intelマニュアル では、整数モジュロのスループットを80から95サイクルと記載しています。

これが高速なハッシュテーブルが配列のサイズに2のべき乗を使っている主な理由です。その後に1サイクルで実行できる上位ビットのマスク処理をするだけです。
2のべき乗使用の際、大きな問題が1つあります。入力データのパターンが多数存在するため、結果的にハッシュ法の衝突が生じることです。例えば、前述のグラフを再び使用しますが、ここでは、数字はランダムではありません。

見てのとおり、google::dense_hash_mapは成層圏へ向かう勢いで上昇しています。dense_hash_mapのパフォーマンスを低下させてしまう入力パターンは何だったのでしょう。単なる連番です。つまり、全ての数字（0、1、2、…、n – 2、n – 1）を挿入したのです。このようなことをするとテーブルに存在しないキーをルックアップするため、処理が非常に遅くなります。存在するキーのルックアップに問題はないのです。つまりテーブルに存在するキーと存在しないキーのルックアップを混ぜながら実行した場合は、あるルックアップが他のルックアップの何千倍も遅いということが発生し得ることになります。

さらに2のべき乗の使用によってパフォーマンスが悪くなる例として、Rustの標準ハッシュテーブルにおいて、1つのハッシュテーブルから別のハッシュテーブルにキーを挿入する際に 誤って二次的 になってしまう場合が挙げられます。このように2のべき乗の使用が見えづらいところであだとなる場合があるのです。

しかし、私のハッシュテーブルにはこのような問題は存在しません。探索回数の上限を設定することによって上のような問題を最適に解決してくれています。不要な再割り当てをする必要もありません。では、私のハッシュテーブルは2のべき乗の使用によって生じる問題に影響されないということなのでしょうか。とは限りません。例えば、実際に過去に遭遇した問題ですが、2のべき乗を使用したハッシュテーブルにポインタを挿入すると全く使用されないスロットがありました。これは、16バイトごとにヒープ割り当てがされているプログラムでポインタをsize_tにreinterpret_castしたハッシュ関数を使用したことが原因でした。そのため、私のテーブルの16スロットの内1スロットしか使用されていませんでした。これは私のハッシュテーブルで使用している2のべき乗を使用すれば誰にでも起こりうる問題です。

使用する入力のタイプに応じた適切なハッシュ関数を選べば問題を解決することは可能です。しかし、必ずしも快適なUXになるとは限りません。ハッシュテーブルを使用する時は常に注意深くなければいけません。動作しかつそんなに遅くないものを使用すればいいのです。だからこそ私は、素数をハッシュテーブルに使用するようにデフォルト設定し、2のべき乗の使用はオプション設定にすることに決めたのです。

なぜ素数は役に立つのでしょうか。数学的な背景を説明することはできませんが、素数は自身以外には約数がないため、異なる剰余になるからだと思っています。例えば、2のべき乗を使用していて、私のハッシュテーブルには32スロットあるとします。そして、16バイトごとにポインタを挿入しようとします（つまり私の数字は全て16の倍数となります）。ここで整数モジュロを実行してテーブルのスロットを探しますが、スロット0とスロット16の2つのスロットしか出してくれません。32は16で割り切れるため、使用可能なスロットは2つしか出てきません。しかし、スロットの数を素数にすれば、このような問題に直面することにはなりません。例えば、37スロットにした場合、16バイトに設定しても異なるスロットを出し、全37スロットを使用することが可能になります（実際に計算してみれば、16の倍数の最初の37個が全て異なるスロットに行くことが分かると思います）。

では、遅い整数モジュロはどのように解消すればいいのでしょうか。私の場合、boost::multi_indexからコピーした技を使っています。コンパイル時定数で全ての整数モジュロを実行します。サイズとして可能な全ての素数を許可するのではなく、代わりに事前に選択した素数の一覧の中で大きい素数へと拡大していきます。そして、テーブルの数字のインデックスを格納します。次に整数モジュロでハッシュ値をスロットに割り当てると、次のように実行されます。

switch(prime_index)
{
case 0:
    return 0llu;
case 1:
    return hash % 2llu;
case 2:
    return hash % 3llu;
case 3:
    return hash % 5llu;
case 4:
    return hash % 7llu;
case 5:
    return hash % 11llu;
case 6:
    return hash % 13llu;
case 7:
    return hash % 17llu;
case 8:
    return hash % 23llu;
case 9:
    return hash % 29llu;
case 10:
    return hash % 37llu;
case 11:
    return hash % 47llu;
case 12:
    return hash % 59llu;
//
// ... more cases
//
case 185:
    return hash % 14480561146010017169llu;
case 186:
    return hash % 18446744073709551557llu;
}

それぞれのケースがコンパイル時定数で整数モジュロを実行しています。どうしてこれがいいのか。定数でモジュロを実行することで、コンパイラはどのようにすれば速く処理できるか分かるのです。実行することで、それぞれのケースのカスタムアセンブリを取得でき、このカスタムアセンブリが整数モジュロよりも高速で処理してくれます。一見変わっていますが、大幅な速度向上となります。

上のグラフを見れば違いは明らかだと思います。素数を使用すると速度は落ちますが、それでも他のハッシュテーブルと比較すると速いのではないでしょうか。その上、ハッシュテーブルが通常直面する問題に陥りにくくなります。もちろん、全く影響がされないわけではありません。もし、どうしても気になるようでしたら、std::mapを厳しい上限付きで使用するといいでしょう。しかし、2のべき乗を使用した際、悪い影響を受ける可能せいがあるので、注意しなければなりません。素数を使用して悪影響が出るケースは、基本的には、意図的に問題のあるキーを作成した場合のみです。

次にセキュリティについて説明します。ハッシュテーブルに対して実行できる賢い攻撃は、衝突しあうキーを挿入することです。どのようにすればいいのか。Webサイトでハッシュテーブルが内部キャッシュに使用されていることが分かっている場合、Webサイトへのリクエスト文を改造して、全リクエストがハッシュテーブルに衝突するようにすればいいのです。これを実行することで、Webサーバの内部キャッシュを遅くすることができ、うまくいけばWebサイトを停止することもできるでしょう。例えば、Googleが内部でdense_hash_mapを使用していることを知っていれば、上記のグラフで見えるとおり連番を挿入が原因で遅くなっているように、連続でWebサイトリクエストをしてキャッシュを乱すことができるでしょう。探索回数の上限を設定すればこの問題は回避できると思うかもしれません。しかし、新たな脅威にさらされます。私が内部で意図的に使用している素数さえ分かれば、私のテーブルが繰り返し探索回数の上限に達し、繰り返しメモリ割り当てをするようにキーを挿入するればいいのです。つまり、新たな脅威によってサーバのメモリ不足が生じてしまうのです。独自に改造したハッシュ関数を使用することで、問題を解決することができますが、どのようにハッシュ関数を改造すればいいのかまでは提案できません。ここで言えるのは、キーを挿入することができる環境においてハッシュテーブルを使用している場合は、std::hashをハッシュ関数としての使用は避けるべきということです。代わりに予測不能で、処理状態を把握できる関数を使うといいでしょう。反対に、もし人は悪意を持たないと思うのであれば、私の素数バージョンのハッシュテーブルを使って値を均等に分散することができ、問題は発生しないと確信できると思います。

でも、自分のハッシュ関数が均等に分散された値を返してくれることが分かっていて、2のべき乗を使用してもハッシュの衝突が生じないと思うのであれば、私の2のべき乗バージョンのハッシュテーブルを使用してください。その場合、ハッシュ関数オブジェクトのhash_policyにtypedefを使用する必要があります。hash_policyが返されたキーの値を実際に持っているので、私はこれを改造ポイントとしてハッシュ関数オブジェクトに入れました。

独自改造したハッシュ関数オブジェクトにtypedefを入れると次のようになります。

struct CustomHashFunction
{
    size_t operator()(const YourStruct & foo)
    {
        // your hash function here
    }
    typedef ska::power_of_two_hash_policy hash_policy;
};

// later:
ska::flat_hash_map<YourStruct, int, CustomHashFunction> your_hash_map;

ここでは、ska::power_of_two_hash_policyをhash_policyとしてtypedefを改造したハッシュ関数で実行します。すると、flat_hash_mapは2のべき乗の使用に切り替わります。さらに、std::hashが使えると分かっているので、power_of_two_std_hashというタイプをstd::hashの呼び出しのみに使用します。しかし、power_of_two_hash_policyを使用します。

1   ska::flat_hash_map<K, V, ska::power_of_two_std_hash<K>> your_hash_map;

どれを使用しても、ハッシュ衝突が少なければ速いハッシュテーブルになります。

挿入や削除のパフォーマンス

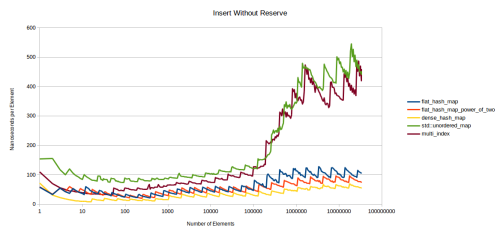
ハッシュテーブル理論について長々と説明してしまいましたが、私のテーブルのパフォーマンスに話を戻しましょう。下のグラフはマップにアイテムの挿入に要した時間を測定したものです。測定方法は、N要素の挿入に要した時間を測定し、要した時間をNで割り平均時間を算出しました。最初のグラフは挿入前にreserve()を呼び出さなかった場合の速度です。

このグラフはギザギザしていますが、異なる方向に向いています。再割り当てに時間を要した場合、平均コストが上昇します。このコストは、再度、再割り当てを実行するまで償却されます。

このグラフのもう1つの点は、左半分にはL3キャッシュに完全に収まる表しかないことです。 私はこれにキャッシュ・ミス・トリガー・テストを書かないことにしました。これは時間がかかる上に、前述の理由から右半分を見るだけでキャッシュミスの良い近似となることが分かったからです。

ここでは、私の新しいハッシュテーブルはgoogle::dense_hash_mapによって打ち負かされますが、それほど差は開いていません。私の新ハッシュテーブルは速いけれども、dense_hash_mapほど速くないというだけです。理由はdense_hash_mapが挿入の際に要素を動かさないからです。単に空いているスロットを探して要素を挿入するだけだからです。私の使用しているロビンフッドハッシュ法は、全てのノードをできるだけ理想の位置に近づけるため、挿入の際に要素を移動します。挿入するために高負荷になってしまうという妥協が伴いますが、ルックアップの方が速くなります。しかし、あまり影響は大きくないので、私は満足しています。

では、次は要素の挿入前にreserve()を呼び出した場合に要した時間です。

最後にノードベースのコンテナに何が起きているのか分かりません。何が起きているのか調査するのは面白いかもしれませんが、私はしていません。私は、使っている標準ライブラリのmalloc関数の呼び出しが原因だと疑っています(Linux gcc)。このグラフや他のグラフなどにおいても非常に時間がかかるといった、測定の問題に直面しました。

全体的に、前のグラフと同じようですが、ギザギザしていません。これは、予備によって再割り当ての必要がなくなるからです。私の挿入も高速ですが、google::dense_hash_mapには及びません。

では最後に要素の削除に要する時間を見てみましょう。このために私はN要素のマップを構築しマップ上の全ての要素をランダムに削除するのに要した時間を測定しました。要した時間をNで割り要素当たりのコストを算出しました。

繰り返しになりますが、ノードベースのコンテナは遅く、フラットコンテナでもほとんど変わりません。私のハッシュテーブルよりもdense_hash_mapの方が若干速いのですが、ほんの少し速いだけです。dense_hash_mapからの削除に要する時間は20ナノ秒で、私のハッシュテーブルからの削除に要する時間は23ナノ秒です。全体的に見るとどちらも高速だと思います。

しかし、大きな違いが1点あります。dense_hash_mapから要素が削除されるとtombstoneがテーブルに残ります。tombstoneは新たに要素を挿入しない限り除去することはできません。tombstoneはgoogle::dense_hash_mapがルックアップの際に実行する二次的探索法の要件です。要素が削除されると、スロット入れる代わりの要素を見つけるのが難しくなります。ロビンフッドハッシュ法で線形探索すれば空いているスロットに入れる要素を見つけるのは簡単です。理想のスロットにない要素を単に前のスロットに移動すればいいのです。二次的探索法の場合、4つ隣のスロットにある要素になるかもしれません。そのスロットの要素が移動された場合、新たに空いたスロットに挿入するノードを再び探す必要が出てきます。代わりにtombstoneを置くことで、この作業を省くことができます。さらにテーブルはルックアップの際にtombstoneは無視すればいいことを分かっています。次の挿入でtombstoneは置き換えられることになります。

tombstoneがテーブルにあるため、速度を若干低下させることになってしまいます。つまりdense_hash_mapは削除後のルックアップの速度を犠牲に速い削除を実現しているのです。影響の度合いを測定するのは難しいのですが、これを可能にするテストを見つけました。要素の挿入と削除の実行を繰り返します。

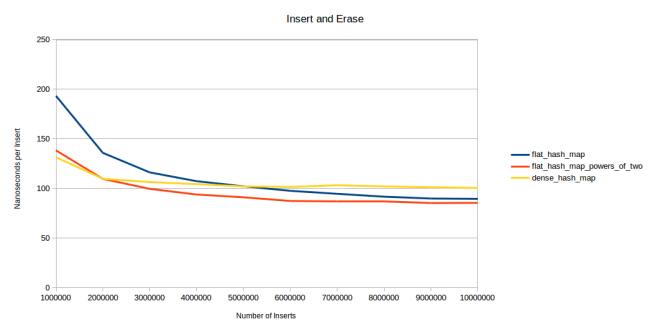
このテストでは、まずランダムなintを100万生成します。そして、これらを繰り返しハッシュテーブルに挿入し削除します。ポイントはランダムに実行することです。例えば、1から4までの4つの整数しかないとします。この時の有効な”挿入と削除の繰り返し”の実行は、1を挿入、3を挿入、1を削除、2を挿入、4を挿入、4を削除、1を挿入、2を削除、3を削除、3を挿入、2を挿入といったようになります。全ての要素が挿入しては削除して、また挿入します。しかし、順番は決まっていません。上のグラフは挿入の数および各要素の挿入に要した時間の測定結果を表示しています。1つ目のデータポイントは左側にあり、100万の要素の挿入を表しています。2つ目のデータポイントは、説明したように100万の要素の挿入および削除、再挿入の不規則な実行を表しています。次のデータポイントは挿入、削除、挿入、削除の実行を表しています。つまり3つのポイントで挿入を実行しています。なんとなく分かったかと思います。

1つ目のデータポイントを見ると挿入が速いため、dense_hash_mapの方が速いことが分かります。2つ目のデータポイントでは、すでに私のハッシュテーブルの速度も追い付いています。そして3つ目のデータポイントでは私のハッシュテーブルが勝っています。また、600万の挿入を実行しても私の素数バージョンが勝っています。私のテーブルの速度が上がっている理由は、削除の方が多いため、テーブルの平均負荷率が低下するからです。頻繁に100万ものアイテムの削除を実行すれば、約50万もの要素がテーブルにある状態となります。つまり、グラフの右の方に行くほど平均してテーブルの要素の数は少ない状態を表します。私のハッシュテーブルはこれを利用することができますが、dense_hash_mapの場合はたくさんのtombstoneがテーブルに残っておりため、これ以上高速になるのを妨げています。それでも、他のハッシュテーブルと比較するとdense_hash_mapはとても高速です。

この観点から考えると、削除後にtombstoneをテーブルに残してしまうことになってもdense_hash_mapが二次的探索法を使用していることが理解できます。それでもテーブルはとても高速で、ノードベースのコンテナよりも断然高速なのです。ここで重要なのは、簡単に空きスロットを探して要素を挿入してくれるため、ロビンフッドハッシュ法で線形探索すればスマートに要素の削除ができることです。もし、頻繁に要素を削除したり挿入したりするテーブルを使う場合は役に立つでしょう。