2017年2月23日
一から学ぶベジェ曲線
(2016-12-29)by Jamie Wong
本記事は、原著者の許諾のもとに翻訳・掲載しております。
(編注:SVGアニメーションを元記事にならい追加しました。リクエストありがとうございました。)
皆さんは線分のことをどう表現しますか? 線分は、端点によって考えられるかもしれません。その端点を P0 、 P1 と呼ぶことにしましょう。
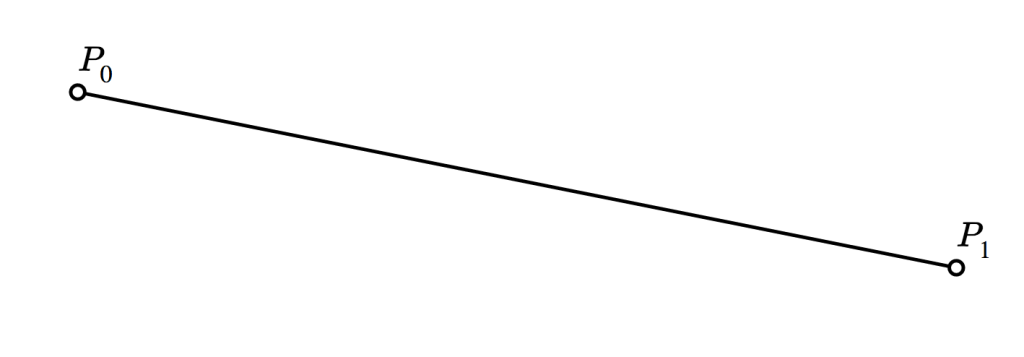
線分を厳密に定義するならば、「 P0 と P1 を結ぶ直線において、 P0 と P1 の間にある全ての点の集合」と言えるかもしれません。これは以下のように表せるでしょう。
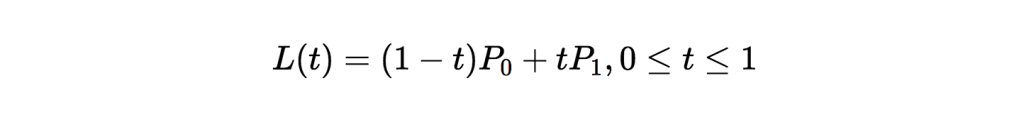
便利なことに、上記の定義から、その線分上のどこにある点の座標でも簡単に求めることができます。例えば、中点は L(0.5) にあります。
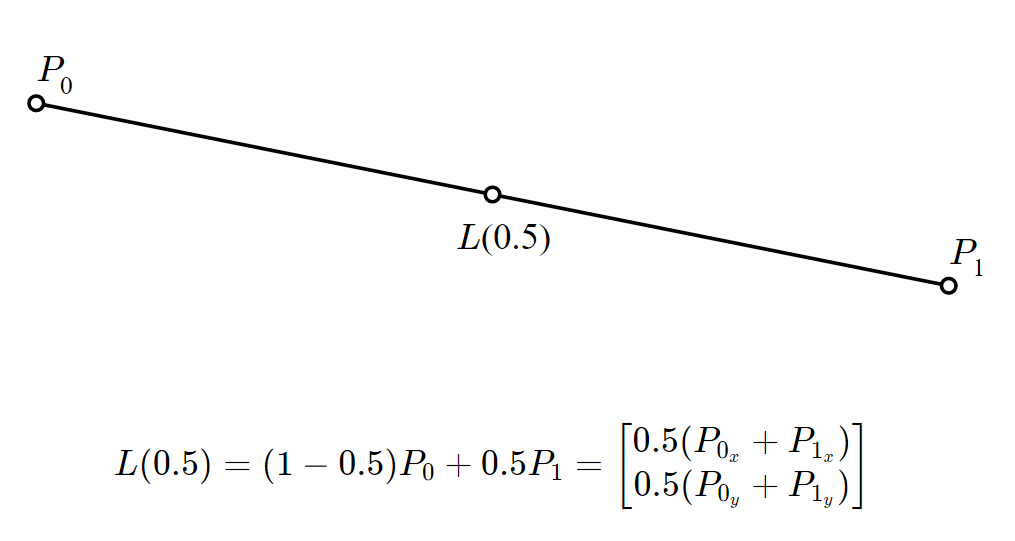
実は、2点間のどんな値でも、任意の精度で 線形補間する ことが可能です。そのため、時間関数 L(t) の t で線をたどるといった、より複雑なことができるのです。
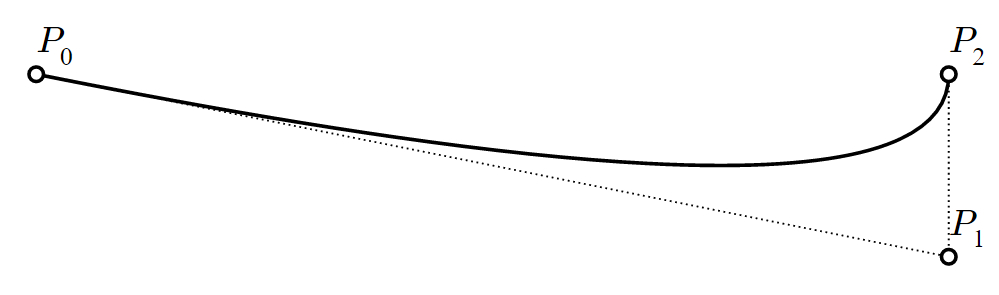
ここまで来ると、「それが曲線と何の関係があるのか?」と不思議に思うかもしれません。2つの点だけで正確に線分を描けるということは、かなり直感的に理解できそうです。では、以下の曲線を正確に描くにはどうすればよいでしょうか?

このような 独特な 曲線も、3つの点だけで描くことができるとわかります!
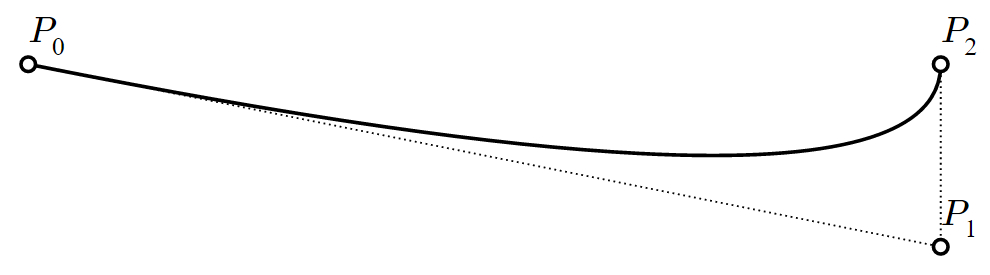
これは2次ベジェ曲線と呼ばれます。この複雑な帽子をかぶっているかのような曲線を得るための線分は1次ベジェ曲線と言えるかもしれません。その理由を見てみましょう。
まず、 P0 と P1 を補間すると同時に P1 と P2 を補間するとどんな形になるか考えてみましょう。
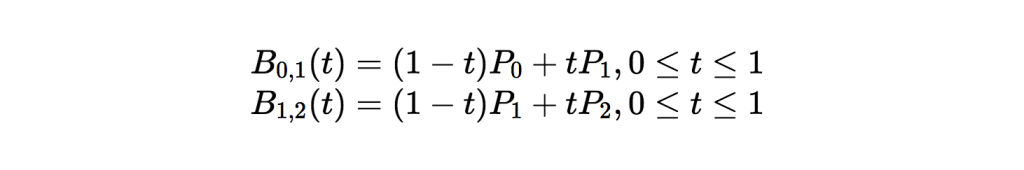
それでは、 B0,1(t) と B1,2(t) の線形補間を行ってみると…
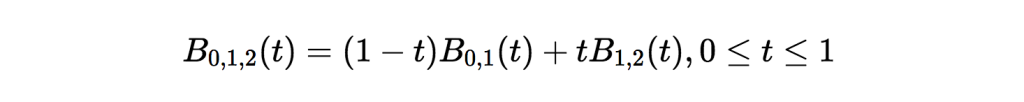
B0,1,2(t) の等式は B0,1 と B1,2 の等式にそっくりなことに注目してください。 B0,1,2(t) のパスをたどるとどうなるか見てみましょう。
先ほどの曲線になりました!
高次のベジェ曲線
2本の1次ベジェ曲線を補間すると2次ベジェ曲線が得られるのと同様に、2本の 2次ベジェ曲線 を補間すると 3次ベジェ曲線 が得られます。
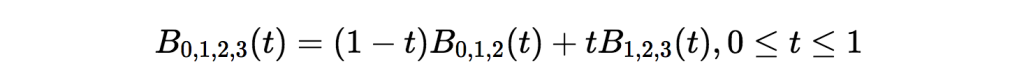
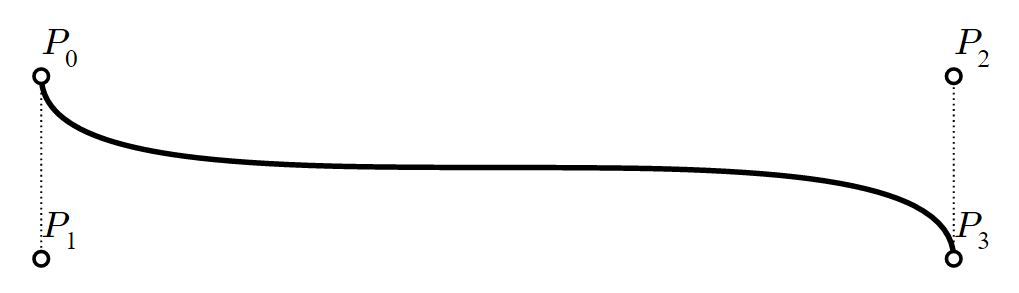
ここで、厄介な再帰的定義が含まれているのではないかと内心疑問が湧くかもしれません。実は、そのとおりなのです。
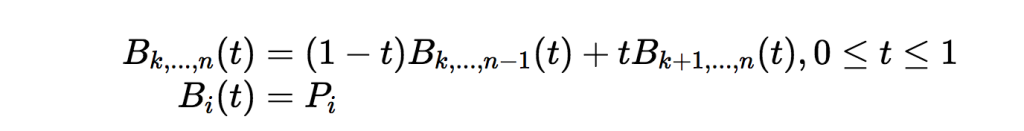
TypeScriptで(簡潔ですが効率の悪い形で)表すと、以下のようになるでしょう。
type Point = [number, number];
function B(P: Point[], t: number): Point {
if (P.length === 1) return P[0];
const left: Point = B(P.slice(0, P.length - 1), t);
const right: Point = B(P.slice(1, P.length), t);
return [(1 - t) * left[0] + t * right[0],
(1 - t) * left[1] + t * right[1]];
}
// Evaluate a cubic spline at t=0.7
B([[0.0, 0.0], [0.0, 0.42], [0.58, 1.0], [1.0, 1.0]], 0.7)ベクタ画像の3次ベジェ曲線
偶然にも3次ベジェ曲線は、単純さと正確さのバランスがうまく取れているので、様々な用途に役立つようです。 Figma のようなベクタ編集ツールで最もよく使われるタイプの曲線です。

Figma での3次ベジェ曲線
2つの塗り潰された丸 ● は P0 と P3 、2つのひし形 ◇ は P1 と P2 だと考えてください。これらは、さらに複雑な曲線ベクタを構成する基本要素です。
フォントグリフは、TrueType(.ttf)フォントのベジェ曲線によって指定されます。

3次ベジェ曲線の vector network として表現された、 Free Serif Italic の小文字の「e」
Scalable Vector Graphics(.svg)ファイルのフォーマットは、ベジェ曲線を2つの 曲線プリミティブ の1つとして使います。曲線プリミティブは、以下の画像の広範囲で使われています。
SVGフォーマットの 3次スプラインの虎
アニメーションの3次ベジェ曲線
ベジェ曲線は、空間的曲線の表現に使われるのはもちろんですが、量間の曲線的関係の表現に使われても何ら不思議はありません。例えば、 x と y の関係を示すのではなく、 CSSのトランジションタイミング関数 は時間の割合が出力値の割合と関連しています。
ベジェ曲線で定義されたトランジションタイミング関数
3次ベジェ曲線は、CSSでタイミング関数を表現する2つの方法のうちの1つです(もう1つは steps() )。CSSのタイミング関数における cubic-bezier(x1, y1, x2, y2) の記法は、3次ベジェ曲線の P1 と P2 の座標を指定するものです。
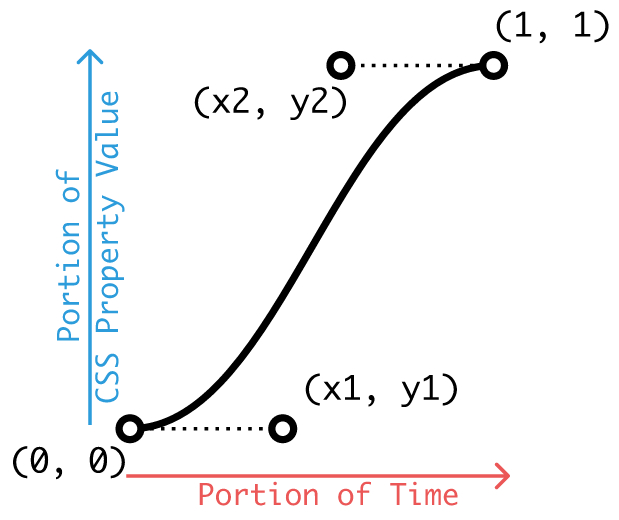
transition-timing-function: cubic-bezier(x1, y1, x2, y2) のグラフ
Portion of CSS Property Value:CSSプロパティ値の割合
Portion of Time:時間の割合
オレンジ色のボールが動いているアニメーションを作成したいとしましょう。以下全てのグラフにおいて、 赤色の線 は一定速度での時間の動きを表しています。
ベジェ曲線を使う理由
ベジェ曲線は、曲線を描くのに役立つ美しい抽象概念です。最もよく使われる形態である3次ベジェ曲線は、曲線を描いて格納するという問題を4つの座標を格納するという問題に変えます。
効率面での利点の他に、4つの制御点を曲線形の上に移すと直感的に理解しやすくなり、直接操作エディタに適したものとなります。
点の2つは曲線の端点となっているので、多くのベジェ曲線を使ってさらに複雑な構造を正確に作り上げることが容易になります。端点が正確に指定されることは、アニメーションの場合は常に大変便利です。イージング関数では、 t=0% の時は初期値、 t=100% の時は最終値なのです。
少し気づきにくい利点は、 P0 と P1 を結ぶ線が、 P0 から出る曲線の接線になっているということです。このため、点対称の制御点を持つ2本の接続した曲線がある場合、接続点の傾きは両側で同じになることが保証されます。

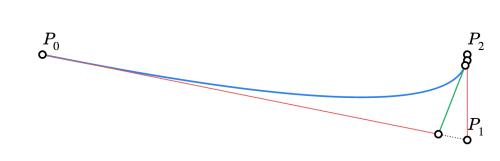
左:点対称の制御点を持つ2本の接続した3次ベジェ曲線。
右:制御点が点対称でない場合。
ベジェ曲線のような数学的概念を扱う主な利点は、自分の問題領域の他の部分では全く認識できない問題に突き当たっても、何十年にもわたる数学研究を利用すれば大抵解決できるということです。
例えば、私は本記事を書くに当たって、上掲の曲線をアニメーション化するため、指定値 t でベジェ曲線を分割する方法を学ばなければなりませんでした。ですが、それに関してうまく説明されている記事「 A Primer on Bézier Curves: Splitting Curves 」(ベジェ曲線入門:曲線を分割する)をすぐに見つけることができたのです。
参考資料と関連記事
- 「 A Primer on Bézier Curves 」(ベジェ曲線入門)は、ド・カステリョのアルゴリズムを使って曲線を描いたり分割したりすることが説明されているだけでなく、かなり包括的な入門書となりそうな無料の電子書籍です。
- Wikipediaの「ベジェ曲線」 には、本記事で取り上げた再帰的定義の他、ベジェ曲線の様々な数式も説明されています。私は、掲載されている独自のアニメーションを見て、ベジェ曲線が極めてエレガントなことを実感しました。
また、Dudley Storeyの記事「 Make SVG Responsive 」(SVGをレスポンシブに)のおかげで、本記事で使ったインラインSVGの全てについて、モバイル環境でもうまく動作するようにできました。