2015年2月17日
パーリンノイズを理解する

(2014-08-09)by Adrian Biagioli
本記事は、原著者の許諾のもとに翻訳・掲載しております。
この記事の目的はKen Perlinの 改良パーリンノイズ を分かりやすく分析し、お伝えすることです。記事内のコードはC#で書かれており、自由にご利用いただけます。最終形のみを見たい方は、 こちらから最終的なソースをご確認ください 。
パーリンノイズは手続き的なコンテンツ生成によく使われる、非常に強力なアルゴリズムです。ゲームや、映画などの視覚媒体に特に有用です。パーリンノイズの開発者であるKen Perlinは、 この最初の実装でアカデミー賞を受賞しました 。彼が2002年に発表した 改良パーリンノイズ について、私はこの記事で掘り下げていきます。パーリンノイズは、ゲーム開発においては、波形の類や、起伏のある素材、テクスチャなどに有用です。例えば手続き型の地形(Minecraftのような地形はパーリンノイズで生成できます)、炎のエフェクト、水、雲などにも使えます。これらのエフェクトのほとんどが2次元、3次元で使用するパーリンノイズを代表するものですが、このノイズはもちろん4次元にも使用可能です。さらに、パーリンノイズは( テラリア や Starbound などに使われている)横スクロールの地形や、手書き線のような画像描写にも使用できます。
また、パーリンノイズを拡張して、時間という新たな次元も表現できます。例えば、2次元のパーリンノイズは地形生成として機能しますが、同様のノイズが3次元では海のうねる波として解釈されます。以下は次元ごとのノイズと実行結果を表にしたものです。
[TABLE]
ご覧の通り、パーリンノイズは自然発生する多くの現象に対して適用できます。ではパーリンノイズのアルゴリズムを数学的および論理的に見ていきましょう。
論理的概要
注:この章は、 Matt Zuckerによって書かれた素晴らしい記事 から多くを引用していることを先に述べさせていただきます。しかし、彼の記事は1980年代初めに書かれた最初のパーリンノイズのアルゴリズムを基にして書かれています。私の記事では2002年に書かれた改良パーリンノイズのアルゴリズムを扱います。従って、私のバージョンとZuckerのバージョンにはいくつか大きな違いがあります。
ではパーリンノイズの基本的な関数からはじめましょう。
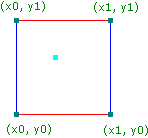
public double perlin(double x, double y, double z);入力としてx、y、zの座標を引数に取り、結果は0.0から1.0の間の double 型で返されます。入力はどのように考えるのでしょうか? まずx、y、zの座標を単位立方体に分割します。つまり立方体の中の座標の位置を見つけるには、 [x,y,z] % 1.0 を求めます。以下の図はこの概念を2次元で表現したものです。
図1:青い点は入力座標を示し、他の4つの点はそれを囲む整数の単位座標を表す ソース
4つ(3Dでは8つ)の単位座標はそれぞれ、 擬似乱数勾配ベクトル と呼ばれるものを生成します。勾配ベクトルは正の方向(ベクトルが指し示す方向)と、当然、負の方向(ベクトルが指し示すのと逆の方向)も定義します。擬似乱数とは勾配ベクトルの方程式に入力された任意の整数に対して、常に同じ結果が出ることを意味します。従って、無作為のように見えても実際は違います。さらにこれは、それぞれの整数座標が、グラディエント関数が同じであれば決して変わらない”固有の”勾配を持つことを意味します。
図2:上の図を元にした勾配ベクトルの例 ( ソース )
しかしながら、上の図は完全に正確ではありません。この記事で扱っているKen Perlinの 改良パーリンノイズ では、これらの勾配は全くの無作為ではありません。立方体の中心点のベクトルから辺に向かって取り出されます。
(1,1,0),(-1,1,0),(1,-1,0),(-1,-1,0),
(1,0,1),(-1,0,1),(1,0,-1),(-1,0,-1),
(0,1,1),(0,-1,1),(0,1,-1),(0,-1,-1)これらの特定の勾配ベクトルの根拠は Ken PerlinのSIFFRAPH 2002の論文 「Improving Noise」 で述べられています。 注:パーリンノイズに関する他の記事の多くは、これらのベクトルを使用していない、改良前のパーリンノイズのアルゴリズムを参照しています。例えば、図2は、改良アルゴリズムが発表される前に書かれたソースを参照しているため、初期のアルゴリズムを示しています。しかしながら、根本的な考え方は同じです。
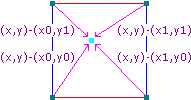
次に、任意の点から格子線上の8つの周囲点へ向かう4つ(3Dでは8つ)のベクトルを計算する必要があります。2次元の場合の例を以下に示します。
図3:距離ベクトルの例 ( ソース )
そして2つのベクトル(勾配ベクトルと距離ベクトル)の間の ドット積 を求めます。これにより最終的な 影響 値が分かります。
grad.x * dist.x + grad.y * dist.y + grad.z * dist.z 2つのベクトルの ドット積 は、それらのベクトルがなす角の余弦とその2つのベクトルの大きさを掛けたものに等しいため、これが成り立ちます。
dot(vec1,vec2) = cos(angle(vec1,vec2)) * vec1.length * vec2.length言い換えると、もし2つのベクトルが同じ方向を指していれば、ドット積は以下のようになります。
1 * vec1.length * vec2.length また2つのベクトルが逆方向を指している場合のドット積は、以下のとおりです。
-1 * vec1.length * vec2.length 2つのベクトルが直交していれば、ドット積は0になります。
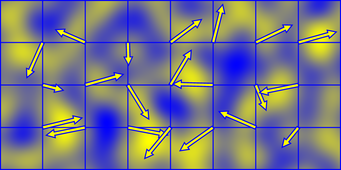
このように勾配の方向と同じであれば、ドット積の結果は正の数となり、逆方向であれば負の数になります。これが勾配ベクトルの正負の定義方法です。この正負の影響を表す図形を以下に表します。
図4:2次元ノイズにおけるベクトルの正負の影響例 ( ソース )
次に、4つ(3Dでは8つ)の格子点の間の加重平均を算出するため、4つの値を補間する必要があります。これを行う方法は簡単です。以下のように平均を出せばいいのです(以下に示すのは2次元の例です)。
// Below are 4 influence values in the arrangement:
// [g1] | [g2]
// -----------
// [g3] | [g4]
int g1, g2, g3, g4;
int u, v; // These coordinates are the location of the input coordinate in its unit square.
// For example a value of (0.5,0.5) is in the exact center of its unit square.
int x1 = lerp(g1,g2,u);
int x2 = lerp(g3,h4,u);
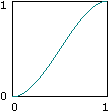
int average = lerp(x1,x2,v);上で述べた加重平均を算出したら、完成まではあと1工程あります。最終結果は線形補間となるため、あまり美しくはなりません。簡単に計算できるものの、不自然に見えます。勾配間はゆるやかな移行が必要です。そこで、フェード関数を使用することにしました。 イーズ曲線 とも呼ばれるものです。
図5:イーズ曲線の例 ( ソース )
上述のコードの例で言うと、このイーズ曲線はuとvの値に適用されます。これにより整数座標に近づくにつれ、ゆるやかに変わります。改良パーリンノイズの実装でのフェード関数は次のようになります。
6t^5 – 15t^4 + 10t^3
理論的な話は以上です。これでパーリンノイズを生成するのに必要とされるコンポーネントは全てそろいました。次はコードに移りましょう。
コード実装
繰り返しになりますが、コードはC#で書かれています。コードは Ken PerlinのJava実装コード に多少変更を加えたバージョンです。ノイズの繰り返し(タイル)を追加しただけではなく、明確さと可読性を上げました。コードはもちろん全て自由にお使いいただけます(私がゼロから書いたわけではありません。Ken Perlinのおかげです)。
設定
まず最初にするべきことは、順列テーブル、つまり p[] 配列を設定することです。単純に0~255の乱数を包含する長さ256の配列です。後でバッファオーバーフローを起こさないように、この配列を繰り返します(全体サイズは512バイト)。
private static readonly int[] permutation = { 151,160,137,91,90,15, // Hash lookup table as defined by Ken Perlin. This is a randomly
131,13,201,95,96,53,194,233,7,225,140,36,103,30,69,142,8,99,37,240,21,10,23, // arranged array of all numbers from 0-255 inclusive.
190, 6,148,247,120,234,75,0,26,197,62,94,252,219,203,117,35,11,32,57,177,33,
88,237,149,56,87,174,20,125,136,171,168, 68,175,74,165,71,134,139,48,27,166,
77,146,158,231,83,111,229,122,60,211,133,230,220,105,92,41,55,46,245,40,244,
102,143,54, 65,25,63,161, 1,216,80,73,209,76,132,187,208, 89,18,169,200,196,
135,130,116,188,159,86,164,100,109,198,173,186, 3,64,52,217,226,250,124,123,
5,202,38,147,118,126,255,82,85,212,207,206,59,227,47,16,58,17,182,189,28,42,
223,183,170,213,119,248,152, 2,44,154,163, 70,221,153,101,155,167, 43,172,9,
129,22,39,253, 19,98,108,110,79,113,224,232,178,185, 112,104,218,246,97,228,
251,34,242,193,238,210,144,12,191,179,162,241, 81,51,145,235,249,14,239,107,
49,192,214, 31,181,199,106,157,184, 84,204,176,115,121,50,45,127, 4,150,254,
138,236,205,93,222,114,67,29,24,72,243,141,128,195,78,66,215,61,156,180
};
private static readonly int[] p; // Doubled permutation to avoid overflow
static Perlin() {
p = new int[512];
for(int x=0;x<512;x++) {
p[x] = permutation[x%256];
}
}p[] 配列は、後でハッシュ関数で使用し、勾配ベクトルを決定します。詳細については後述します。
次に、パーリンノイズ関数を書き始めます。
public double perlin(double x, double y, double z) {
if(repeat > 0) { // If we have any repeat on, change the coordinates to their "local" repetitions
x = x%repeat;
y = y%repeat;
z = z%repeat;
}
int xi = (int)x & 255; // Calculate the "unit cube" that the point asked will be located in
int yi = (int)y & 255; // The left bound is ( |_x_|,|_y_|,|_z_| ) and the right bound is that
int zi = (int)z & 255; // plus 1. Next we calculate the location (from 0.0 to 1.0) in that cube.
double xf = x-(int)x;
double yf = y-(int)y;
double zf = z-(int)z;
// ...
}上記のコードは見ての通りです。まず、変数 repeat よりも入力座標が超過していればオーバーフローが起きるように、モジュロ(剰余)演算子を使用します。次に変数 xi, yi, zi を用意します。これらは座標を含む単位立方体を表します。また、座標は[0,255]の包括的範囲に限定し、 p[] 配列にアクセスするときにオーバーフローエラーにならないようにします。実はこれには残念な副作用があります。パーリンノイズは常に全ての座標を繰り返してしまうのです。しかしパーリンノイズでは小数点座標がありえるため、この繰り返しは問題ではありません。そして最後に単位立方体内部の座標の位置を求めます。基本的には n = n % 1.0 となり、 n は座標を表します。
フェード関数
今度は上記(図5)に書かれているフェード関数を定義する必要があります。先程も書いたとおり、これはパーリンノイズのフェード関数です。
6t5-15t4+10t3
コード内では以下のように定義されます。
public static double fade(double t) {
// Fade function as defined by Ken Perlin. This eases coordinate values
// so that they will ease towards integral values. This ends up smoothing
// the final output.
return t * t * t * (t * (t * 6 - 15) + 10); // 6t^5 - 15t^4 + 10t^3
}
public double perlin(double x, double y, double z) {
// ...
double u = fade(xf);
double v = fade(yf);
double w = fade(zf);
// ...
}u、v、wの値は後から補間して使用します。
ハッシュ関数
パーリンノイズのハッシュ関数は、入力する全座標の固有値を得るために使用されます。Wikipediaでは、 ハッシュ関数 は以下のように定義されています。
…あるデータが与えられた場合にそのデータを代表する数値を得る操作、または、その様な数値を得るための関数のこと。
これはパーリンノイズが使用しているハッシュ関数です。前に作成した p[] のテーブルを使っています。
public double perlin(double x, double y, double z) {
// ...
int aaa, aba, aab, abb, baa, bba, bab, bbb;
aaa = p[p[p[ xi ]+ yi ]+ zi ];
aba = p[p[p[ xi ]+inc(yi)]+ zi ];
aab = p[p[p[ xi ]+ yi ]+inc(zi)];
abb = p[p[p[ xi ]+inc(yi)]+inc(zi)];
baa = p[p[p[inc(xi)]+ yi ]+ zi ];
bba = p[p[p[inc(xi)]+inc(yi)]+ zi ];
bab = p[p[p[inc(xi)]+ yi ]+inc(zi)];
bbb = p[p[p[inc(xi)]+inc(yi)]+inc(zi)];
// ...
}
public int inc(int num) {
num++;
if (repeat > 0) num %= repeat;
return num;
}上のハッシュ関数は、入力座標を囲む8つの単位立方座標全てをハッシュします。 inc() は単に数を増やしてノイズが繰り返しているかを確かめるために使っています。繰り返しできるかどうかの確認が必要なければ、 inc(xi) を xi+1 に置き換えられます。ハッシュ関数の結果は p[] 配列により0から255の間(包括的)の値となります。
グラディエント関数
私はこれまでずっと、Ken Perlinの改良前の grad() 関数は不必要に複雑で混乱しやすいものだと思っていました。思い出してください。 grad() の目的は、無作為に選択された勾配ベクトルと8つの位置ベクトルのドット積を計算することです。Ken Perlinは、ビットを反転させるコードを使ってこれを計算しました。
public static double grad(int hash, double x, double y, double z) {
int h = hash & 15; // Take the hashed value and take the first 4 bits of it (15 == 0b1111)
double u = h < 8 /* 0b1000 */ ? x : y; // If the most significant bit (MSB) of the hash is 0 then set u = x. Otherwise y.
double v; // In Ken Perlin's original implementation this was another conditional operator (?:). I
// expanded it for readability.
if(h < 4 /* 0b0100 */) // If the first and second significant bits are 0 set v = y
v = y;
else if(h == 12 /* 0b1100 */ || h == 14 /* 0b1110*/) // If the first and second significant bits are 1 set v = x
v = x;
else // If the first and second significant bits are not equal (0/1, 1/0) set v = z
v = z;
return ((h&1) == 0 ? u : -u)+((h&2) == 0 ? v : -v); // Use the last 2 bits to decide if u and v are positive or negative. Then return their addition.
}上のコードをもっと分かりやすい(しかも多くの言語でもっと速く書ける)書き方にすると、以下のようになります。
// Source: http://riven8192.blogspot.com/2010/08/calculate-perlinnoise-twice-as-fast.html
public static double grad(int hash, double x, double y, double z)
{
switch(hash & 0xF)
{
case 0x0: return x + y;
case 0x1: return -x + y;
case 0x2: return x - y;
case 0x3: return -x - y;
case 0x4: return x + z;
case 0x5: return -x + z;
case 0x6: return x - z;
case 0x7: return -x - z;
case 0x8: return y + z;
case 0x9: return -y + z;
case 0xA: return y - z;
case 0xB: return -y - z;
case 0xC: return y + x;
case 0xD: return -y + z;
case 0xE: return y - x;
case 0xF: return -y - z;
default: return 0; // never happens
}
}上のコードのソースは、 こちら で確認いただけます。どのような場合でも、この2つのコードは同じ働きをします。どちらも以下の12のベクトルから無作為に1つのベクトルを選択します。
(1,1,0),(-1,1,0),(1,-1,0),(-1,-1,0),
(1,0,1),(-1,0,1),(1,0,-1),(-1,0,-1),
(0,1,1),(0,-1,1),(0,1,-1),(0,-1,-1)これはハッシュ関数の値の最後の4ビット(grad()の1番目のパラメータ)によって決まります。他の3つのパラメータは位置ベクトル(ドット積に用いられるもの)を表しています。
全てを組み合わせる
今度はここまでの全ての関数を使って、周りの8つの単位立方座標を補間し、つなげます。
public double perlin(double x, double y, double z) {
// ...
double x1, x2, y1, y2;
x1 = lerp( grad (aaa, xf , yf , zf), // The gradient function calculates the dot product between a pseudorandom
grad (baa, xf-1, yf , zf), // gradient vector and the vector from the input coordinate to the 8
u); // surrounding points in its unit cube.
x2 = lerp( grad (aba, xf , yf-1, zf), // This is all then lerped together as a sort of weighted average based on the faded (u,v,w)
grad (bba, xf-1, yf-1, zf), // values we made earlier.
u);
y1 = lerp(x1, x2, v);
x1 = lerp( grad (aab, xf , yf , zf-1),
grad (bab, xf-1, yf , zf-1),
u);
x2 = lerp( grad (abb, xf , yf-1, zf-1),
grad (bbb, xf-1, yf-1, zf-1),
u);
y2 = lerp (x1, x2, v);
return (lerp (y1, y2, w)+1)/2; // For convenience we bind the result to 0 - 1 (theoretical min/max before is [-1, 1])
}
// Linear Interpolate
public static double lerp(double a, double b, double x) {
return a + x * (b - a);
}複数のオクターブを利用する
最後に、パーリンノイズをさらに自然に見えるようにする方法について議論したいと思います。パーリンノイズがある程度自然な振る舞いを実現させることは確かですが、自然界で見られるような不規則性を完全に表現できるわけではありません。例えば地形には、山などのように大きく広範囲に広がる特徴や、丘やくぼ地くらいの規模のもの、また石や岩などの細かい特徴、そして非常に小さなものでは小石など、地形の中ではごくわずかな差となるものまであります。これに対しての解決策は非常にシンプルです。周波数や振幅を変えた複数のノイズ関数を使い、これらを合成するのです。もちろん、周波数とはサンプリングされるデータの周期のことで、振幅とは結果が表す範囲のことです。
図6:周波数と振幅を変えたノイズの結果6例 ( ソース )
これらの結果を合成すると、以下のようになります。
図7:上の結果を合成したもの ( ソース )
明らかに、この結果の方がはるかに説得力がありますね。上の6つのノイズは、異なるノイズの オクターブ を呼び出したものです。連続するそれぞれのオクターブが最終結果に与える影響はどんどん小さくなっていきます。もちろん、オクターブが1つ増えるごとにコード実行時間は線形増加しますので、実行時(例えば60fpsで実行する手続き型の炎のエフェクトなど)には数オクターブ以上使おうとしない方がいいでしょう。しかし、オクターブはデータの前処理(地形の生成など)の時は最高です。
では、連続したそれぞれのオクターブは どのくらいの 影響力を持つのでしょうか。これを決めるのは、パーシステンスと呼ばれる、また別の値です。 Hugo Elias は、パーシステンスを以下のように定義しています。
frequency = 2^i
amplitude = persistence^i
ここでは、iが問題のオクターブを表しています。コード内の実装はシンプルです。
public double OctavePerlin(double x, double y, double z, int octaves, double persistence) {
double total = 0;
double frequency = 1;
double amplitude = 1;
double maxValue = 0; // Used for normalizing result to 0.0 - 1.0
for(int i=0;i<octaves;i++) {
total += perlin(x * frequency, y * frequency, z * frequency) * amplitude;
maxValue += amplitude;
amplitude *= persistence;
frequency *= 2;
}
return total/maxValue;
}結論
以上で説明は終わりです。これでノイズを作れるようになりました。 ここで全てのソースコードを参照できます 。もし疑問点があれば、下のコメント欄で質問してください。
参考文献
もし興味があれば、下の参考文献をチェックしてみてください。
* Ken Perlin’s “Official” Improved Perlin Noise ―これはKen Perlinが書いた最初のアルゴリズムです。
* “The Perlin Noise Math FAQ” ―これはアルゴリズムについての理論的なリファレンスとしてすばらしいものです。しかしこちらは私がこの記事で使用したアルゴリズムではなく、80年代に書かれた 最初の パーリンノイズのアルゴリズムを用いていることにご注意ください。
* Hugo Elias’ article ―パーリンノイズについての最も有名な記事の1つです。これはオクターブやパーシステンス、現実世界におけるパーリンノイズの使用に関する優れた参考文献です。しかし、 これは本当のパーリンノイズではありません 。Hugoのアルゴリズムはパーリンノイズのように勾配に基づいたものではないのです。これはバリューノイズと呼ばれるもので、実質的にはホワイトノイズをぼかしたものです。混乱しないでくださいね。
* “How to use Perlin Noise in Your Games” – Devmag ―パーリンノイズの潜在的な利用方法についての、なかなか良い記事です。読み物としては非常に面白いですが、 こちらも本当のパーリンノイズではありません 。この記事の中でDevmagが使っているのはバリューノイズです。
* GPU Gems – “Implementing Improved Perlin Noise” ―この記事はパーリンノイズを使ってリアルタイムに美しい海の景色をレンダリングするのに、GPUのものすごいパワーを利用するというものです。シェーダはすごいですね。
読んでいただきありがとうございました!
更新
2014/9/8―記事を更新しました。ドット積についてより分かりやすい説明を入れ、また記事内の誤字を修正しました。redditの r/programming 、 r/gamedev 、 r/Unity3D でアドバイスをくださった皆さん、本当にありがとうございます。