2017年3月17日

できる動的計画法：ロッド切り出し問題

Dynamic Programming for the confused : Rod cutting problem

(2017-2-13)by Pratik Anand

本記事は、原著者の許諾のもとに翻訳・掲載しております。

私が常に頭を悩まされていたのが最適化問題です。これは、コードを理解するだけでも非常に困難な問題です。そこで、これまでに私が学んだことを基に、典型的な動的計画法の問題を取り扱ういくつかの記事を投稿することにしました。今回取り上げるロッド切り出し問題は古典的な最適化問題であり、動的計画法の一例と言えます。

ロッド切り出し問題とは？

ロッド切り出し問題は、現実世界で私たちが直面するたいていの問題に非常によく似ています。ある長さの棒があり、この棒を最大利益が得られる長さにして切り売りをしたいという状況があると仮定します。ここで問題となるのは、切り出した長さによって棒の値段が異なる点です。例えば細かく切り出した方が大まかに切り出した場合よりも、より多くの利益が得られる可能性があるため、ちょっと違った考え方をする必要があります。

先に進む前に、まずはこの問題をより正確に定義しておきましょう。

長さ n > 0 の棒がある。これを k (k ≤ n) 本に切り出し、切り出された各棒の長さを i 、価格を p(i) 、各棒から得られる最大利益を r(i) （本数は複数の可能性あり）とする。この場合の長さ n に対する r(n) を求めよ。

棒の長さi	棒の価格p(i)
1	1
2	5
3	8
4	9
5	10
6	17
7	17
8	20
9	24
10	30

長さに対する価格を表示した表

考察の過程

問題を煮詰めると、結局どこで棒を分割するかという問題に行き着くことがわかります。

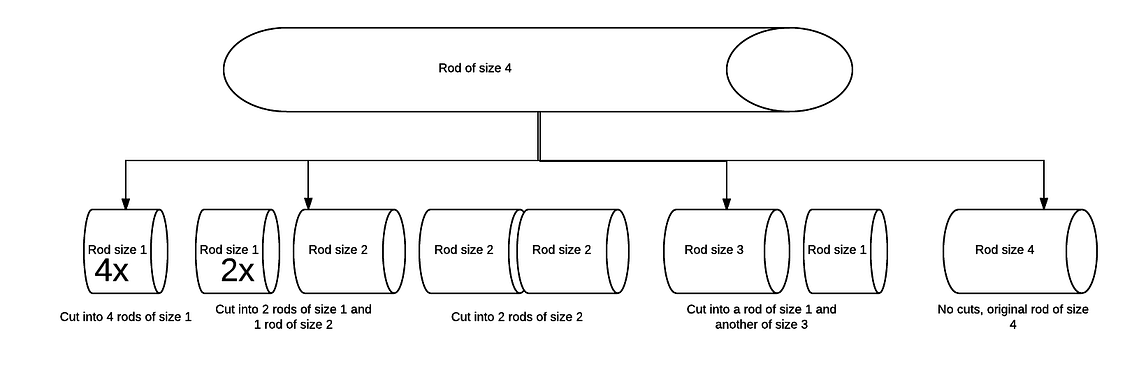
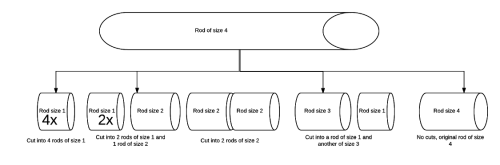
最大利益 r(4) を得られるのは、棒を何本に切り出した場合か？

長さ1の棒が4本（3箇所で切断） = 4 x p(1) = 4 x 1 = **4**

長さ1の棒が2本と長さ2の棒が1本（2箇所で切断） = 2 x p(1) + 1 x p(2) = 2 x 1 + 5 = **7**

長さ2の棒が2本（1箇所で切断） = 2 x p(2) = 2 x 5 = **10**

長さ1の棒が1本と長さ3の棒が1本（1箇所で切断） = 1 x p(1) + 1 x p(3) = 1 + 8 = **9**

元々の長さ4の棒（切断なし） = 1 x p(4) = 9

このことから、最大利益は10であり、size=2の部分で分割して棒を長さ2になるように2本切り出しした場合であるとわかります。

まとめると、長さ i = n の棒の最大利益 r(n) は、以下のように求められます。

長さ i=1 から始めて、長さ i=n に達するまで以下2と3のステップを繰り返す
長さ i の棒を切断するかどうか決める（2つの異なるケースに分岐が発生）
残りの棒 (n-i) について、手順1からステップを実行
以上で発生した全てのケースについて r(n) を算出する
算出された r(n) の最大値が、最大利益となる。どこで切り出されたかをトラッキングするには、追加容量が必要。

このケースにおいて、再帰は理想的な候補の1つです。再帰的なコードはこちらをご覧ください。

時間計算量とは何か？

この問いに対する答えは、切り分ける方法が何通りあるかを考えることで得られます。

長さ n の棒を1箇所で切断する場合、 (n-1)C(1) 通りの方法があります。

2箇所で切断する場合＝ (n-2) C(2) 通り

k箇所で切断する場合＝ (n-k)C(k) 通り

まとめると次のようになります：

1箇所で切断する場合＋2箇所で切断する場合＋…k箇所で切断する場合…n-1箇所で切断する場合

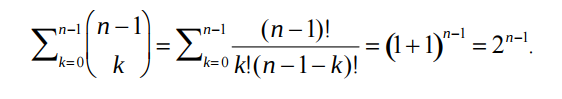
ソース： http://www.cs.uml.edu/~kdaniels/courses/ALG_503_F12/DynamicRodCutting.pdf

このように、時間計算量は指数関数的になりますが、もっと良い方法があるか見てみましょう。

1つの方法として、再帰を メモ化 、すなわちメモを取るという方法があります（説明はこちら。しかし依然として、大きな値であるnに対しては機能しなくなってしまう指数関数的な演算は残ってしまいます。

それでは、動的計画法について考えましょう。

動的計画法で解決する

この問題では既に、 部分構造最適性と部分問題重複性 が明らかになっています。

最大収益であるr(i)は、棒に対して0, 1, ….(i-1)箇所で切断を行うことで求められます。

r(i) = max { p(i), p(1)+r(i-1), p(2)+r(i-2)….p(i-1)+r(1) }

これを説明すると、r(i)は棒を切断しない場合のp(i)であるか、あるいは長さ1に切断した場合の価格をr(i-1)に加えた価格であると読むことができます。なおこのr(i-1)は、事前に解決した、i-1の長さの棒の最大収益に該当します（切断の回数はさらに多くなる場合があります）。長さ2の場合も同様にして、r(i-2)について解けばよいことがわかります。つまり、r(i)は、iより小さい値に対して事前に算出された値に依存します。しかしこの場合は貪欲法とは異なり、決定を下すために全ての分析を行います。実際、元に戻って、全てのiの値を比較します。これは 個々の部分問題の最適値によって次の部分問題を解決するという、部分問題重複性なので、部分構造最適性となります。

計算式

r(1) = p(1) = 1（長さ1で切断し、それ以上の切断はなし）

r(2) = max{ p(2), p(1)+r(1)} = max(5, 2) = 5 （長さ2で切断し、それ以上の切断はなし）

r(3) = max{p(3), p(1)+r(2), p(2)+r(1)} = max(8, 1+5, 5+1) = 8 （長さ3で切断し、それ以上の切断なし）

r(4) = max{p(4), p(1)+r(3), p(2)+r(2), p(3)+r(1)} = max(9, 1+8, 5+5, 8+1) = 10 (長さ2で切断)

r(5) = max{p(5), p(1)+r(4), p(2) +r(3), p(3)+r(2), p(4)+r(1)} = max(10, 1+10, 5+8, 8+5, 9+1) = **13 **(長さ2で切断)

このまま続けていくと…

表を埋めてみると以下のようになります。

	1	2	3	4	5
p(i)	1	5	8	9	10
r(i)	1	5	8	10	13
cut	1	2	3	2	2

完成した表

r(5)の最終的な答えは13になります。

ここで13という答えが導き出されるまでに何回切断したかを数えるにはどうしたらいいでしょうか。

難しく考えずに、r(5)の計算式から順にさかのぼって（バックトラックして）いけばいいのです。

r(5)のcut value（訳注：上表のcut行参照）には2とあるので、どこかで切断して長さ2の棒があるはずです。つまりそこで1回切断されたことになります。

長さ5に対して長さ2の棒があるので、残りは長さ3になります。そこでr(3)を確認してみましょう。cut valueが3とありますから、この長さ3はこれ以上短く切断されていないことになります。

よって長さ2では切断は1回だけでいいというわけです。

長さ5の棒から得られる最大利益は1箇所だけ切断して、長さ2と長さ3の棒に切り出した時となります。

この非再帰的なアプローチはボトムアップな方法です。その際の時間計算量は次のようになります。

T(n) = T(n-1) + T(n-2) +…..+T(1) + 1

T(1)=1
T(2) = T(1) + 1= 2
T(3) = T(2) + T(1)+ 1 = 2 + 1 + 1 
T(n) = n + n-1 + n-2 + …等差数列
T(n) = O(n²)

O(2^n)と比べると O(n²)のほうがはるかに効率的です。

今回の方法では最適化問題の解決のための直観力を養うことはできますが、すべての最適化問題に有効なわけではありません。しかし、とっかかりとするにはちょうど良いでしょう。

参考までに、動的計画法の関連リンクについても掲示しておきます：