2017年1月16日
グラフ代数
(2016-12-05)by Andrey Mokhov
本記事は、原著者の許諾のもとに翻訳・掲載しております。
数学や計算幾科学の分野において、 グラフ理論 は私のお気に入りのテーマです。この記事では、私が長年研究している グラフ代数 についてご紹介します。代数学は私にとって、グラフを扱う上で欠かせないツールになっています。皆さんにも、その便利さが伝われば幸いです。
私がグラフ代数の研究を始めたきっかけは、CONCUR 09という学会向けに提出した論文です。その論文は不採録でしたが、私はその後も特定用途向けのいくつかの論文を発表し、代数学の知識を深めていきました。その全容が記載された論文は、 ACM TECS でご確認いただけます(査読前の原稿は こちら です)。では早速、最もシンプルなグラフ代数の概要と、Haskellでの実装方法を紹介します。
グラフの作成
ここでは、固定領域に存在する頂点を持つ一式のグラフをGと表記します。例として、正整数の頂点を持つグラフについて考えてみましょう。グラフg ∈ Gは、(V, E)のペアで表現されます。Vはグラフに含まれる頂点の集合で、E ⊆ V × Vはグラフの辺集合です。
最も単純なグラフは 空 グラフです。この空グラフを数式の中ではεで、Haskellのコード内では empty と表記します。つまり、ε = (∅, ∅)、ε ∈ Gと書きます。
単一の頂点vが含まれるグラフは、単純にvと表記します。例えば、1 ∈ Gは単一の頂点1を含むグラフで、({1}, ∅)と表します。Haskellでは、任意の頂点をグラフの一つとして扱うために vertex を使用します。
上記の基本要素から、より大きなグラフを構成するためには、 overlay(重ね合わせ) と connect(連結) の二項演算子を使用します。それぞれ+と→の記号で表記します。以下は、2つのグラフのoverlay(+)の定義です。
(V1, E1) + (V2, E2) = (V1 ∪ V2, E1 ∪ E2)
つまり、2つのグラフのoverlayは、単純に頂点と辺の和集合になります。同様に、connect(→)の定義は以下のようになります。
(V1, E1) → (V2, E2) = (V1 ∪ V2, E1 ∪ E2 ∪ V1 × V2)
overlayと違って、2つのグラフをconnectする場合は、左の変数に含まれる各頂点から右の変数に含まれる各頂点に対して引いた辺を加えます。以下に、いくつか例を示します。
- 1+2は、2つの独立した頂点1と2を含むグラフ。
- 1→2は、頂点1と2をつなぐ有向辺を含むグラフ。
- 1→(2+3)は、3つの頂点{1, 2, 3}と、2つの有向辺(1, 2)、(1,3)を含むグラフ。Haskellでは、
connect 1 (overlay 2 3)と表記します。 - 1→1は、頂点1と 閉路 (1つの頂点が辺の始点かつ終点になっているループ)を含むグラフ。
上記のグラフをHaskellで表現すると、次のようになります。
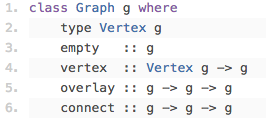
class Graph g where
type Vertex g
empty :: g
vertex :: Vertex g -> g
overlay :: g -> g -> g
connect :: g -> g -> gでは、いくつかグラフを作成してみましょう。connectされていない任意の頂点のリストを含むグラフは、次のように作成できます。
vertices :: Graph g => [Vertex g] -> g
vertices = foldr overlay empty . map vertex以下は、任意の頂点のリストから成る クリーク (あらゆる頂点のペアが連結されているグラフ)です。
clique :: Graph g => [Vertex g] -> g
clique = foldr connect empty . map vertex例えば、 clique [1..] は、すべての正整数を対象とする無限のクリークです。このように全空間を網羅するクリークを 完全グラフ と呼びます。さらに、 辺のリスト からも次のように任意のグラフを作成できます。
fromEdgeList :: Graph g => [(Vertex g, Vertex g)] -> g
fromEdgeList = foldr overlay empty . map edge
where
edge (x, y) = vertex x `connect` vertex y次のセクションで説明するように、グラフはいくつかの法則を満たし、 半環 によく似た代数的構造を形成しています。
代数的構造
先ほど紹介した構造(G, +, →, ε)は、次のようなさまざまな一般法則を満たします。
- (G, +, ε)は冪等性可換 モノイド 。
- (G, →, ε)はモノイド。
- →は+に対して分配法則を満たす。例、1 → (2 + 3) = 1 → 2 + 1 → 3
グラフ代数が半環と違う点は、以下の 分配法則 のみです。
x → y → z = x → y + x → z + y → z
実際、半環においては、2つの演算子にはそれぞれ異なる単位元があります。ここでは、それらをε+ とε→で表記します。この2つが等価であることを、分配法則を使って証明してみましょう。
| ε ₊ | = | ε ₊ → ε _(→) → ε _(→) | (→の単位元) |
| = | ε ₊ → ε _(→) + ε ₊ → ε _(→) + ε _(→) → ε _(→) | (分配法則) | |
| = | ε ₊ + ε ₊ + ε _(→) | (identity of →) | |
| = | ε _(→) | (+の単位元) |
分配法則によって+の冪等性も得られます。
以下は、グラフ代数を表現するための最小限の公理です。
- +には可換性と結合性がある。
- (G, →, ε)はモノイドである。例、→には結合性があり、εは単位元。
- →は+に対して分配法則を満たす。
- →は展開可能:x → y → z = x → y + x → z + y → z
読者への練習問題:上記の最小限の公理から、εが+の単位元であることを証明してください。これは簡単な問題ではありません。さらに、+が冪等であることも証明してください。
なお、有向グラフから無向グラフに切り替えるには、→の交換性の公理を追加するだけです。この内容については 別のブログ記事 で説明します。
例
ここで、前のセクションの公理を満たす Graph 型クラスの基本的なインスタンスを2つ取り上げましょう。1つ目は Relation というインスタンスで、これはoverlayとconnectの演算子セットに対する定義を満たします。つまり フリーな (他の法則は一切適用されない)インスタンスです。
data Relation a = Relation { domain :: Set a, relation :: Set (a, a) }
deriving (Eq, Show)
instance Ord a => Graph (Relation a) where
type Vertex (Relation a) = a
empty = Relation Set.empty Set.empty
vertex x = Relation (Set.singleton x) Set.empty
overlay x y = Relation (domain x `Set.union` domain y)
(relation x `Set.union` relation y)
connect x y = Relation (domain x `Set.union` domain y)
(relation x `Set.union` relation y
`Set.union` Set.fromDistinctAscList
[ (a, b) | a <- Set.elems (domain x)
, b <- Set.elems (domain y) ])さらに、便宜上+と の演算子を使えるように、 Relation を Num*型のクラスのインスタンスにします。
instance (Ord a, Num a) => Num (Relation a) where
fromInteger = vertex . fromInteger
(+) = overlay
(*) = connect
signum = const empty
abs = id
negate = id注: Num の法則 abs x * signum x == x が成り立つのは、x → ε = xであるためです。実際、どの Graph インスタンスも、必要に応じて Num インスタンスにできます。では、インタラクティブなGHCを使用してグラフを扱ってみましょう。
λ> 1 * (2 + 3) :: Relation Int
Relation {domain = fromList [1,2,3], relation = fromList [(1,2),(1,3)]}
λ> 1 * (2 + 3) + 2 * 3 == (clique [1..3] :: Relation Int)
True基本的な代数的データ型にグラフのコンストラクタをすべて組み入れると、別のシンプルなインスタンスが得られます。
data Basic a = Empty
| Vertex a
| Overlay (Basic a) (Basic a)
| Connect (Basic a) (Basic a)
deriving Show
instance Graph (Basic a) where
type Vertex (Basic a) = a
empty = Empty
vertex = Vertex
overlay = Overlay
connect = Connect生成された Eq インスタンスは代数学の法則に明らかに反するため、ここでは使用できません。例えば、 Overlay Empty Empty は構造的に Empty とは異なります。ただし、以下のようにカスタムの Eq を実装することは可能です。
instance Ord a => Eq (Basic a) where
x == y = toRelation x == toRelation y
where
toRelation :: Ord a => Basic a -> Relation a
toRelation = foldBasic
foldBasic :: (Vertex g ~ a, Graph g) => Basic a -> g
foldBasic Empty = empty
foldBasic (Vertex x ) = vertex x
foldBasic (Overlay x y) = overlay (foldBasic x) (foldBasic y)
foldBasic (Connect x y) = connect (foldBasic x) (foldBasic y)Basic インスタンスの利点は、複雑に連結したグラフをコンパクトに表現できることです。例えば clique [1..n] :: Basic Int の場合、メモリ内のデータ表現は線形サイズになりますが、 clique [1..n] :: Relation Int は各辺を別々に保存するため、必要なメモリは O(n ² ) になります。別のブログ記事でも紹介しますが、辺のリストを処理する既存のグラフアルゴリズムに比べて、コンパクトなグラフ表現を利用して生成したアルゴリズムでは、複雑なグラフを漸近的に高速処理することができます。
まとめ
この記事で紹介したグラフ代数は非常に便利なので、私は長年にわたりさまざまなプロジェクトに活用してきました。 後続のブログ記事 では、無向グラフや推移閉包グラフ(別名、 半順序グラフ、依存性グラフ )、グラフ群、さらにこれらの多様な組み合わせを扱うためのさまざまな代数学を紹介しています。その内容はどれも、複数の公理を拡張することで導かれるものです。
また、現在開発中の alga というグラフ代数を実装したHaskellのライブラリを、近日リリース予定です。この記事に載せたコードスニペットの改善案がありましたら、ぜひお聞かせください。

